Методика и содержание подготовки учащихся к олимпиадам по программированию. Дистанционный курс. Геометрия

Вид материала

Документы

Подобный материал:

• Методика и содержание подготовки учащихся к олимпиадам по программированию. Дистанционный, 119.52kb.
• Программа разработана на основе авторской программы Белошистой А. В. Пояснительная, 96.55kb.
• Дистанционный курс подготовки к егэ по математике, 48.14kb.
• Методика проектирования инструмента. Содержание рабочего чертежа на него. Формы, геометрия, 172.74kb.
• Курс предпрофильной подготовки учащихся с ориентацией на информационно-технологический, 59.17kb.
• Дистанционный курс Современные технологии открытого образования Занятие, 92.07kb.
• Фейгина Евгения Алексеевна, Методист моу дод «цит» Г. Кировск 2010 содержание содержание, 534.9kb.
• Пояснительная записка Курс предназначен для учащихся 9-х классов общеобразовательных, 47.51kb.
• Дистанционный курс «Немецкий язык для студентов заочной формы обучения» Тип эвм: Intel, 617.94kb.
• Элективный курс по геометрии для учащихся 9 классов «Геометрия вокруг нас», 87.42kb.

Геометрия

Обычно олимпиадные задачи редко выходят за границы двухмерного случая. По крайней мере это касается олимпиад для школьников, хотя в студенческих турах иногда встречаются задачи о геометрии в пространстве, но это скорее исключение чем правило. Цель данной главы – охватить по возможности большинство тем, которые необходимо знать школьнику для успешного решения олимпиадных задач в данной области.

Большинство формул будут даны без строгого математического доказательства, тем более что на «правильный» рассказ такой объемной темы может просто не хватить времени, отпущенного в рамках школы.


Расстояние между двумя точками


Пусть даны две точки на плоскости A(x_a, y_a) и B (x_b, y_b). Тогда расстояние между ними будет определяться по теореме Пифагора:




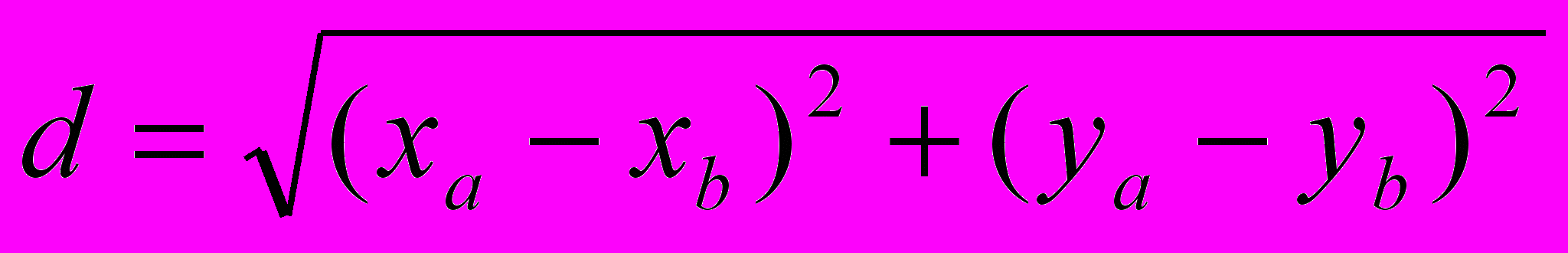
Скалярное произведение векторов


Пусть даны два вектора 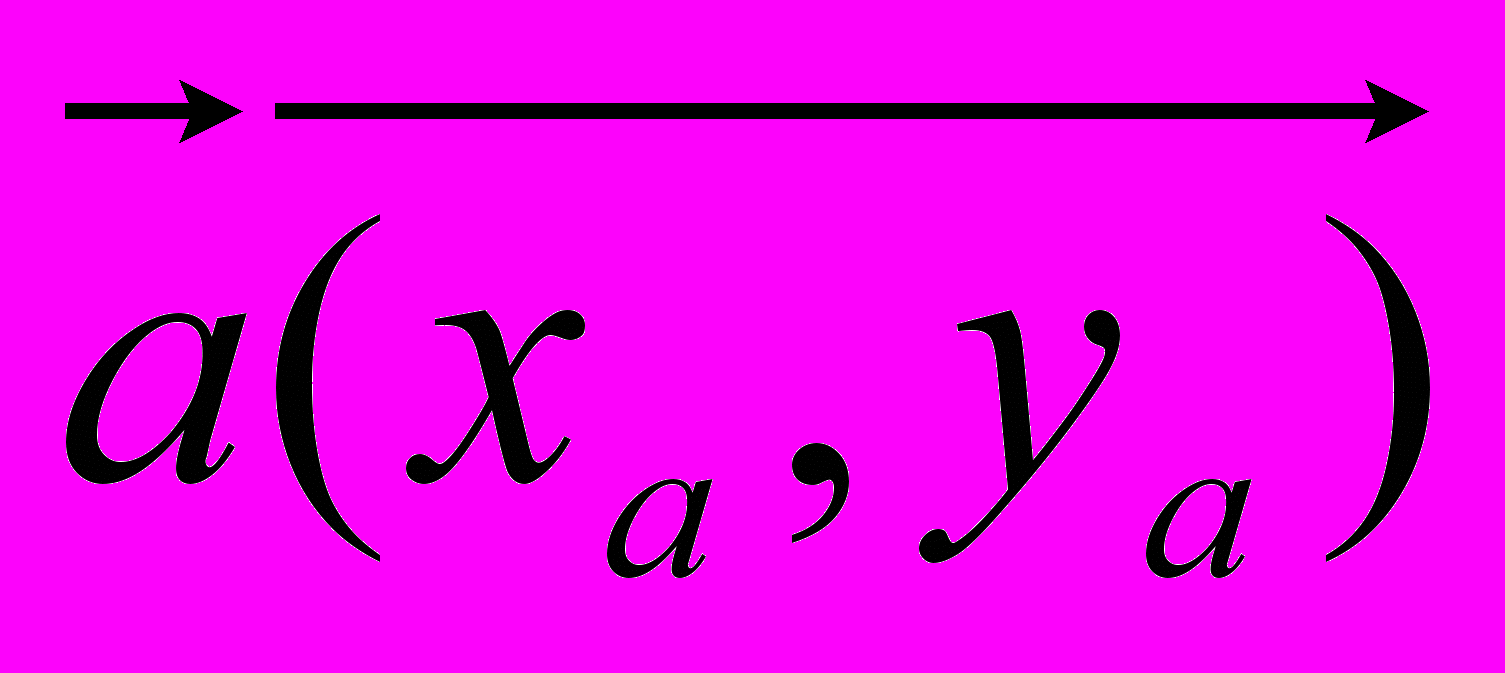и 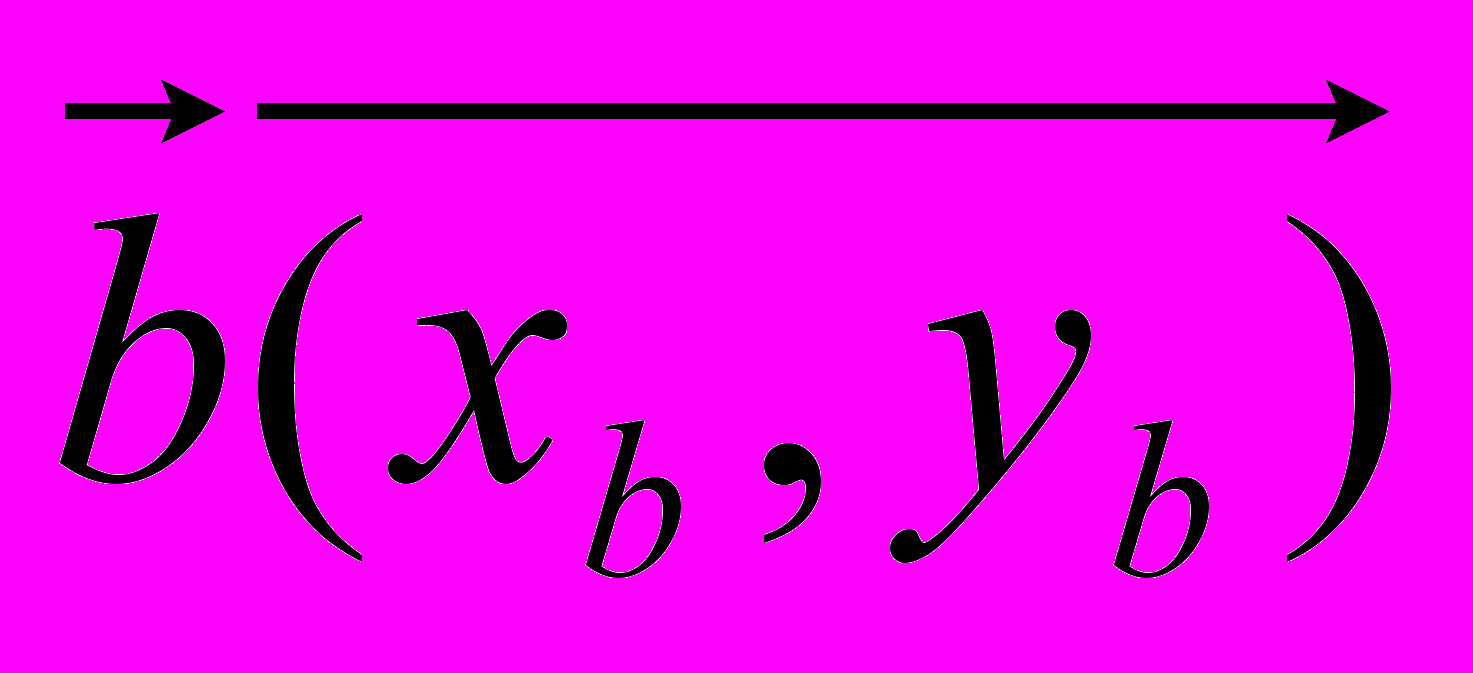. Тогда их скалярное произведение определяется как сумма произведений соответствующих координат:

,

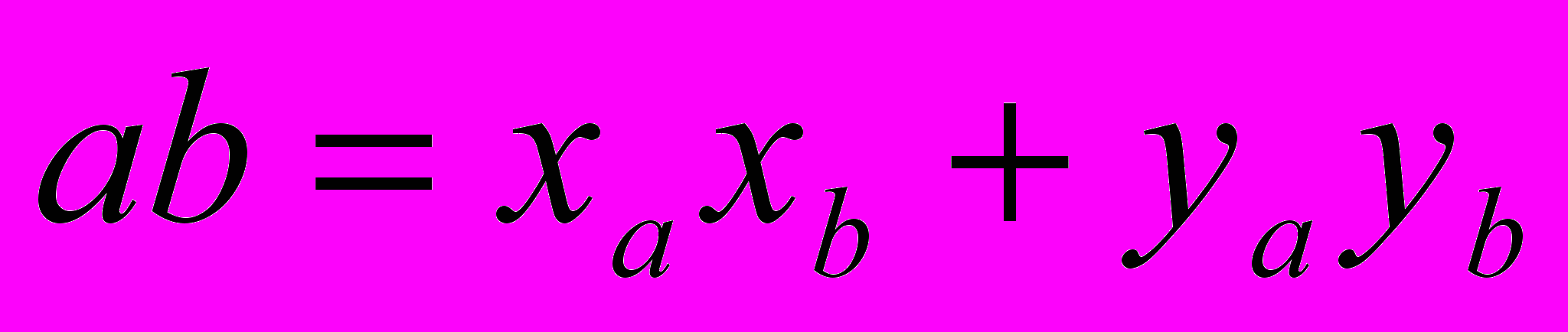по свойству скалярного произведения

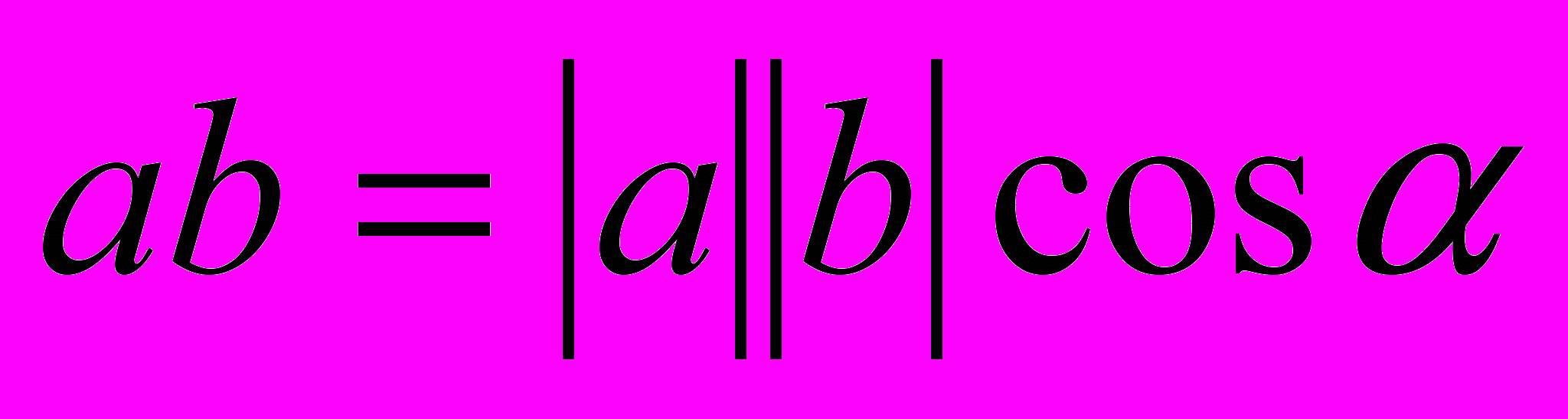, где - длина вектора a, 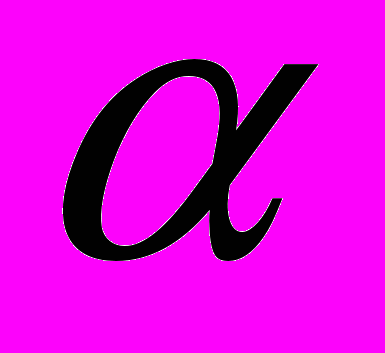- угол между направлениями векторов a и b.

Данное свойство может применяться:

1. для проверки перпендикулярности двух прямых или отрезков. Если две прямые перпендикулярны друг другу, то это же относится и к любым векторам, лежащим на этих прямых. Поскольку угол 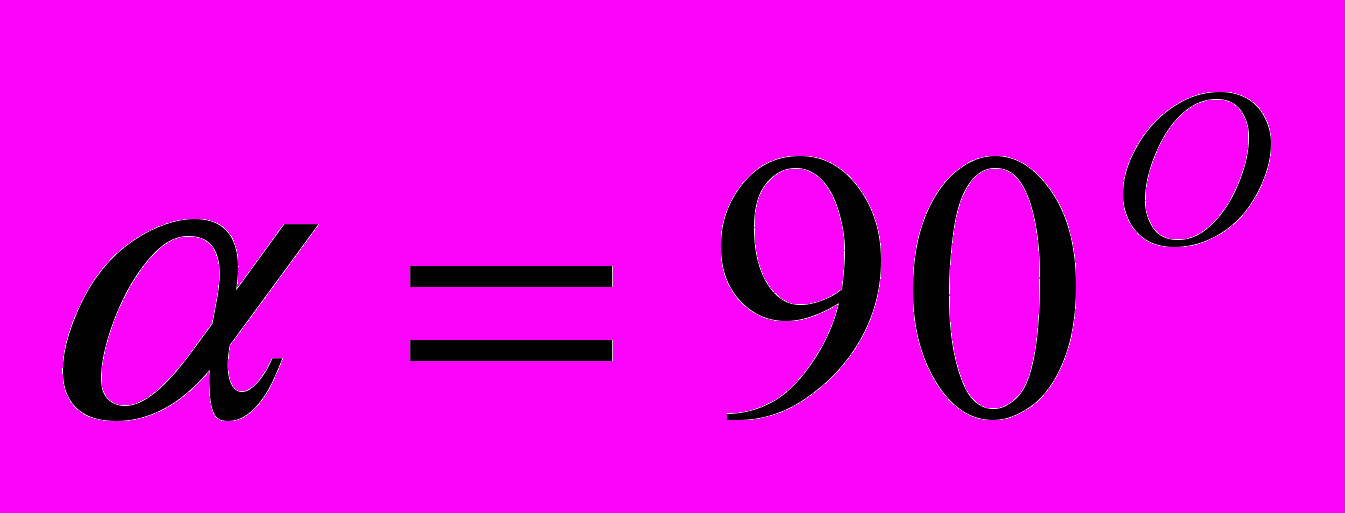, то 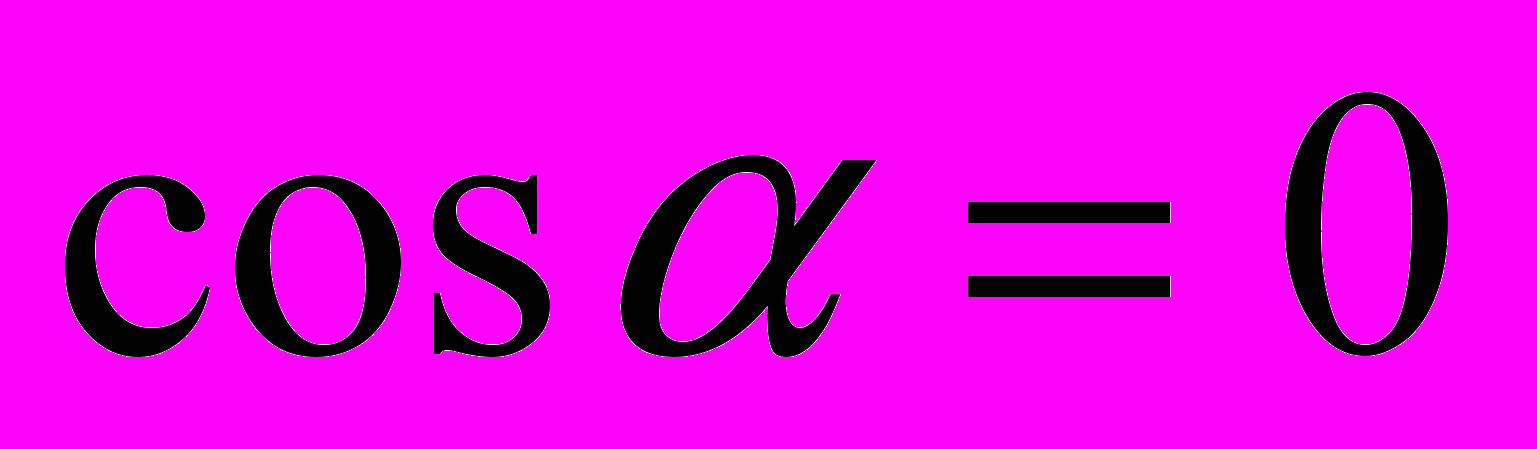, то есть скалярное произведение векторов должно быть равно нулю;
   
2. для нахождения угла между векторами. Если угол 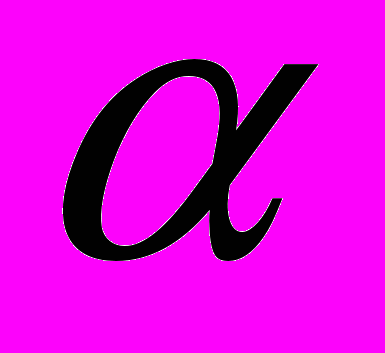- острый, то его косинус будет положительным и скалярное произведение также будет положительно. Если угол 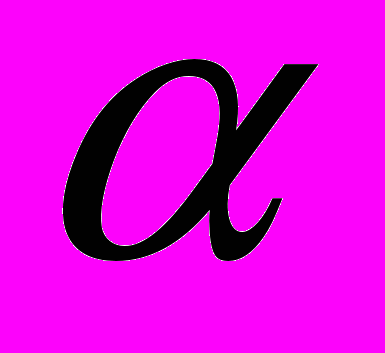- тупой, то и его косинус будет отрицательным и скалярное произведение также будет отрицательно.
   

Некоторые технические особенности


В условии большинства геометрических задач требуется «вывести ответ с точностью до определенного знака после запятой». На практике это означает, что ответ, выданный программой школьника должен отличаться от эталонного не более чем на единицу заданного разряда. К примеру, требование вывести ответ с точностью до 0,001 означает, что ответ, выданный программой школьника должен отличаться от эталонного не более чем на 0,001. То есть при выводе данных округление производить либо не нужно вовсе, либо округлять, но не грубее чем указано в условии задачи.


Также следует учесть, что практических во всех реализациях основных языков все углы измеряются в радианах (как те, что необходимо подставлять в функции sin() или cos(), так и те, что будут возвращены функцией арктангенса - arctan()). Плюс к этому, набор тригонометрических функций в том же Borland Pascal не так велик. К примеру, отсутствуют функции tg(), ctg(), arcsin() и arccos(). Поэтому при отсутствии должной математической подготовки у школьника в области тригонометрии придется ее восполнить. Особое внимание стоит обратить на функцию arctan(x), которая возвращает угол в диапазоне (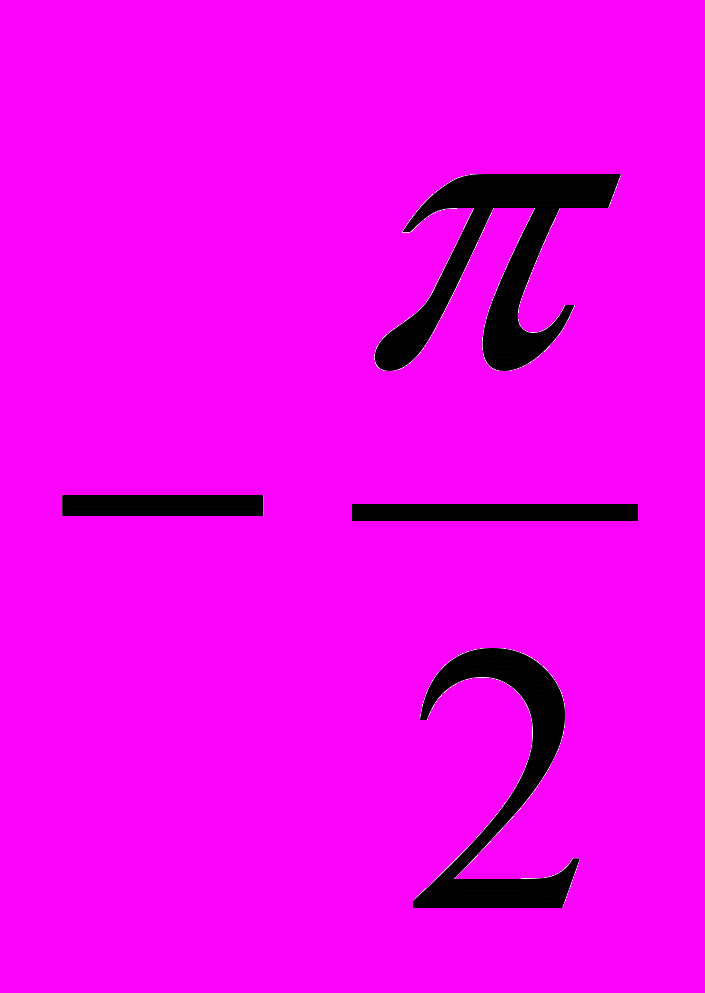; 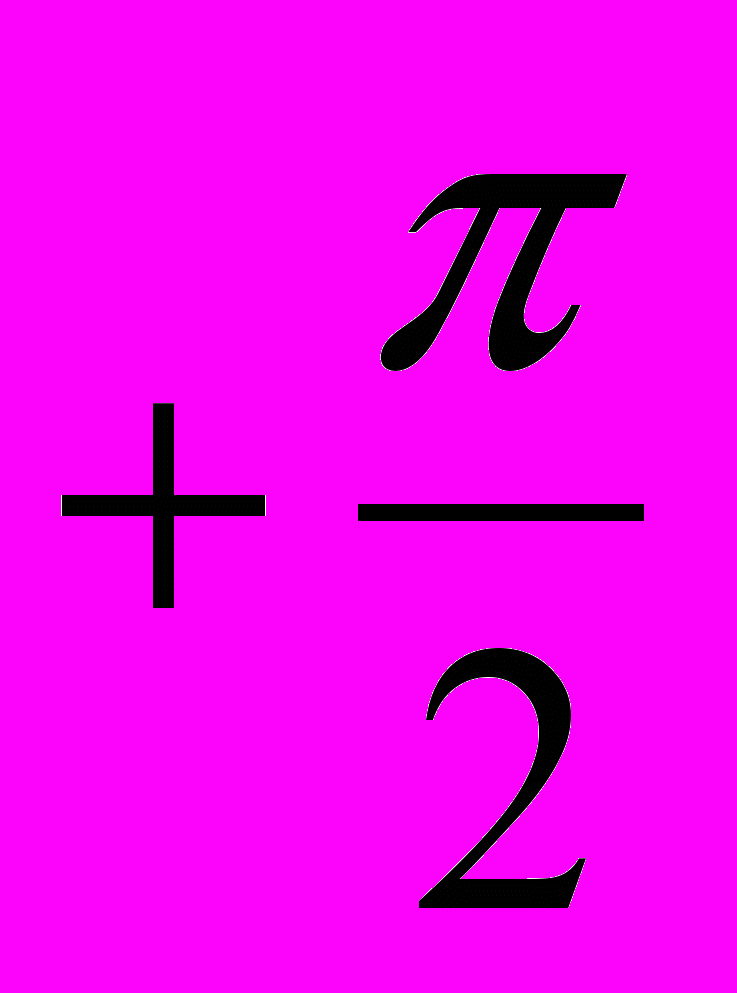), тангенс которого равен заданному x. Рассмотрим это более подробно.


Нахождение полярного угла точки


П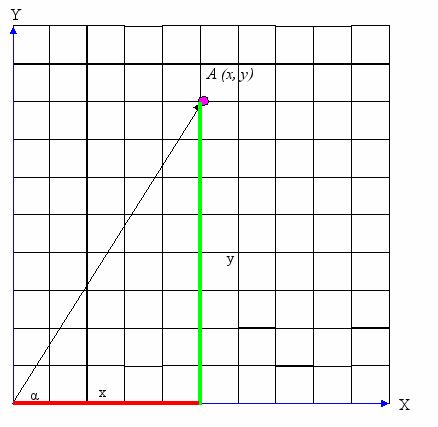усть точка A задана своими координатами (x, y). Требуется определить угол α между радиус-вектором, проведенным из начала координат в точку A и осью Ox.

Очевидно, что в данном случае 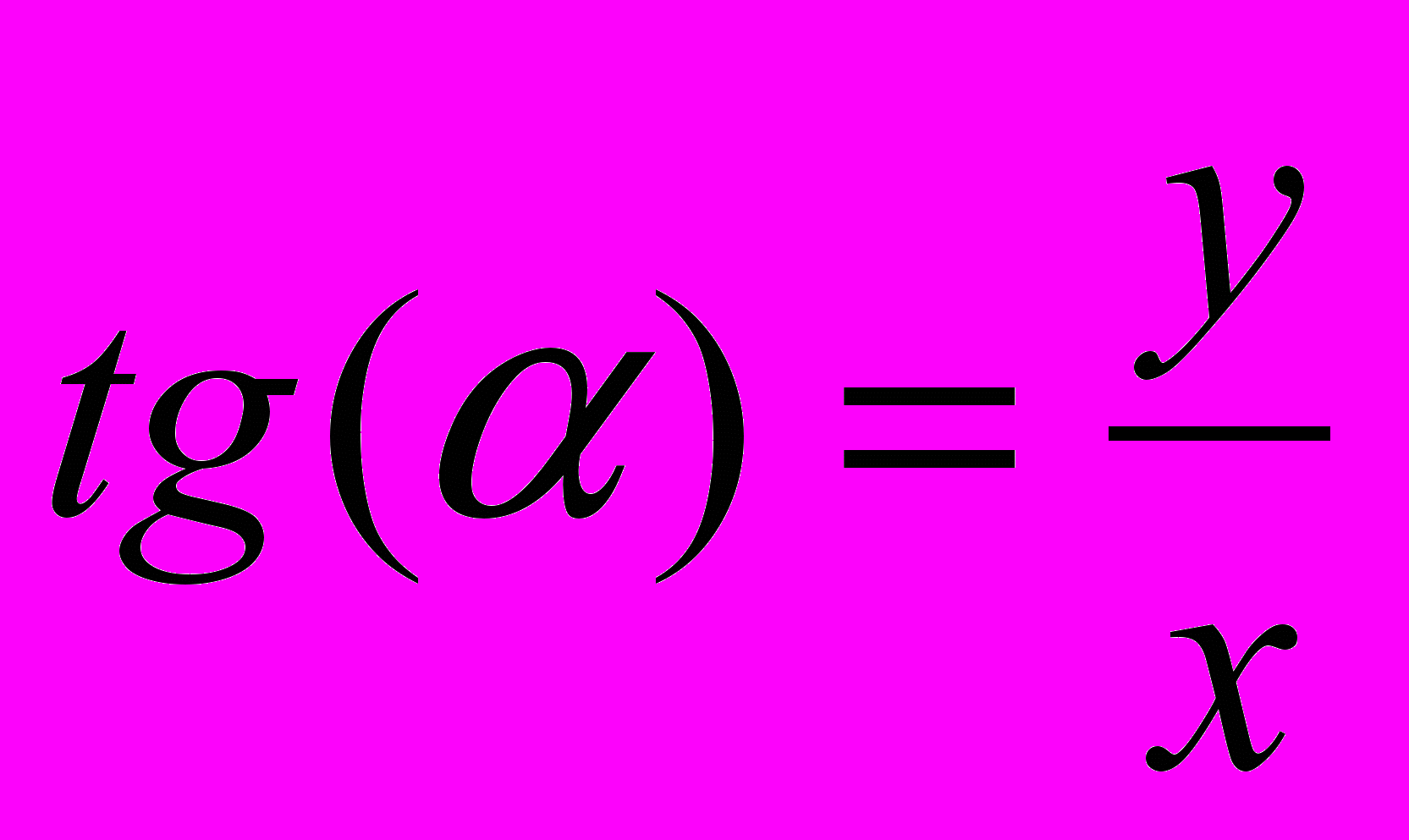, следовательно для начала можно написать формулу 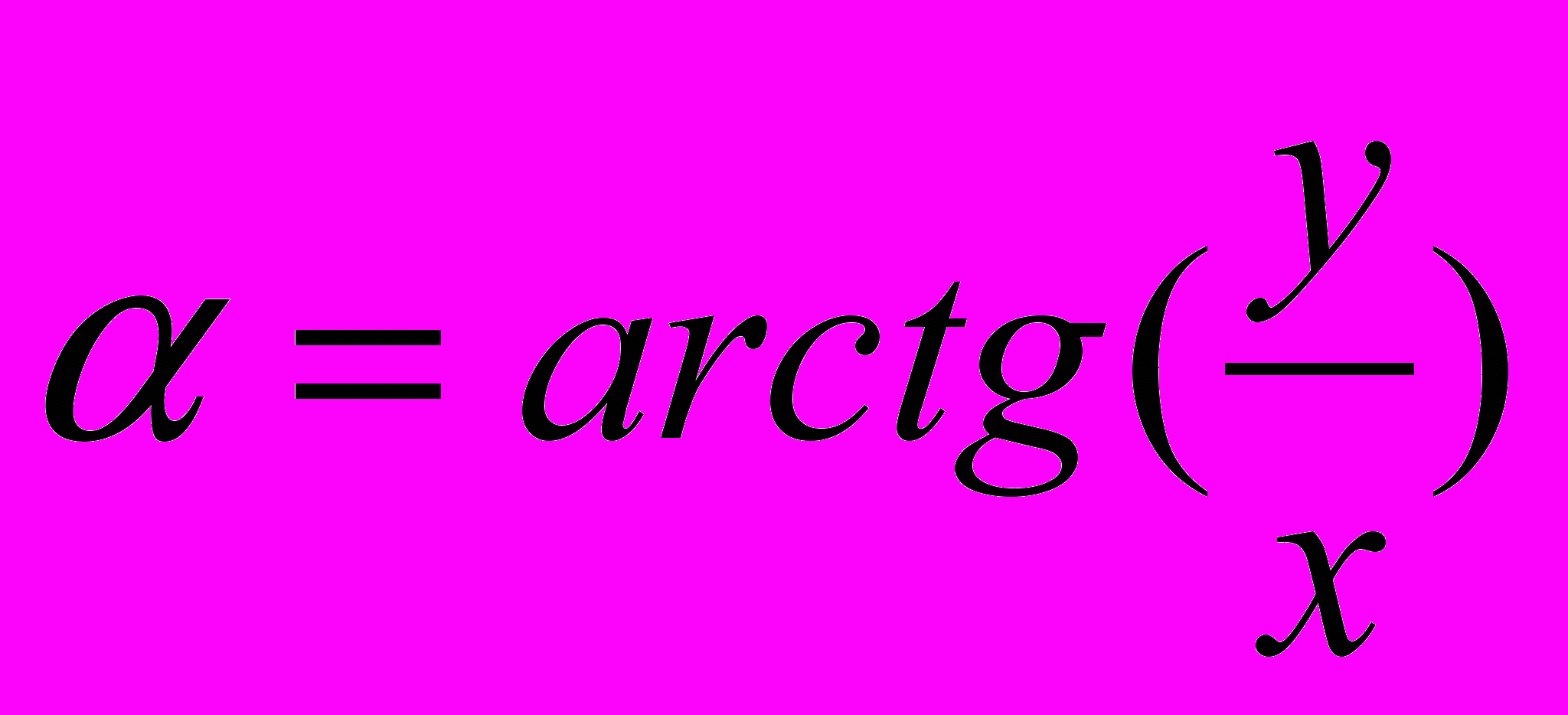. Также следует предусмотреть случаи, когда x=0, и то, что полярный угол может не лежать в интервале (; ).

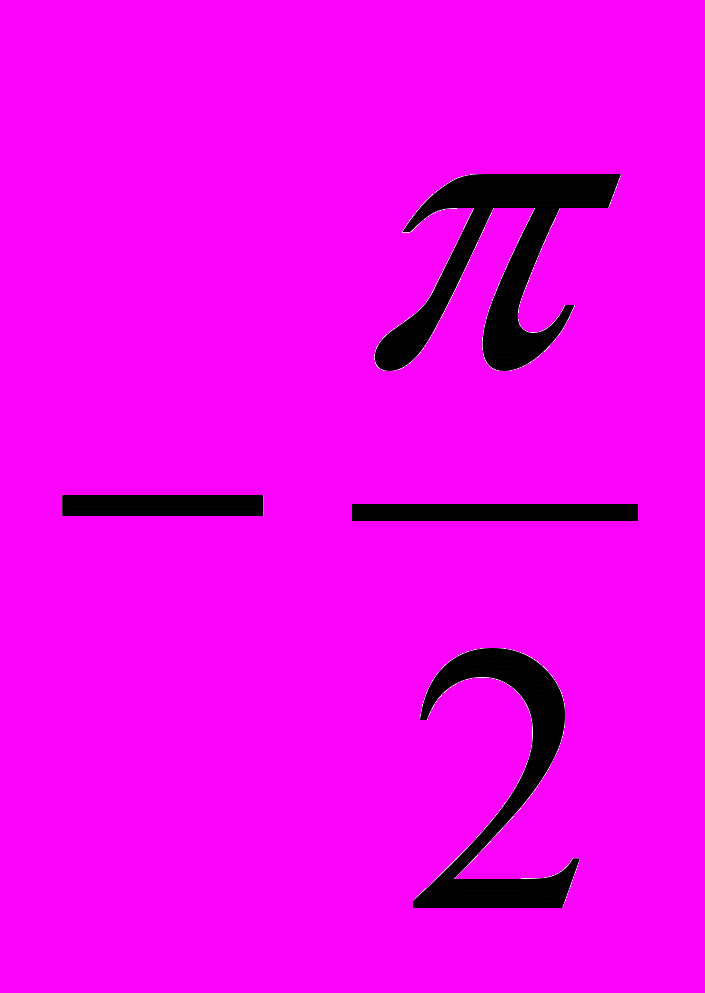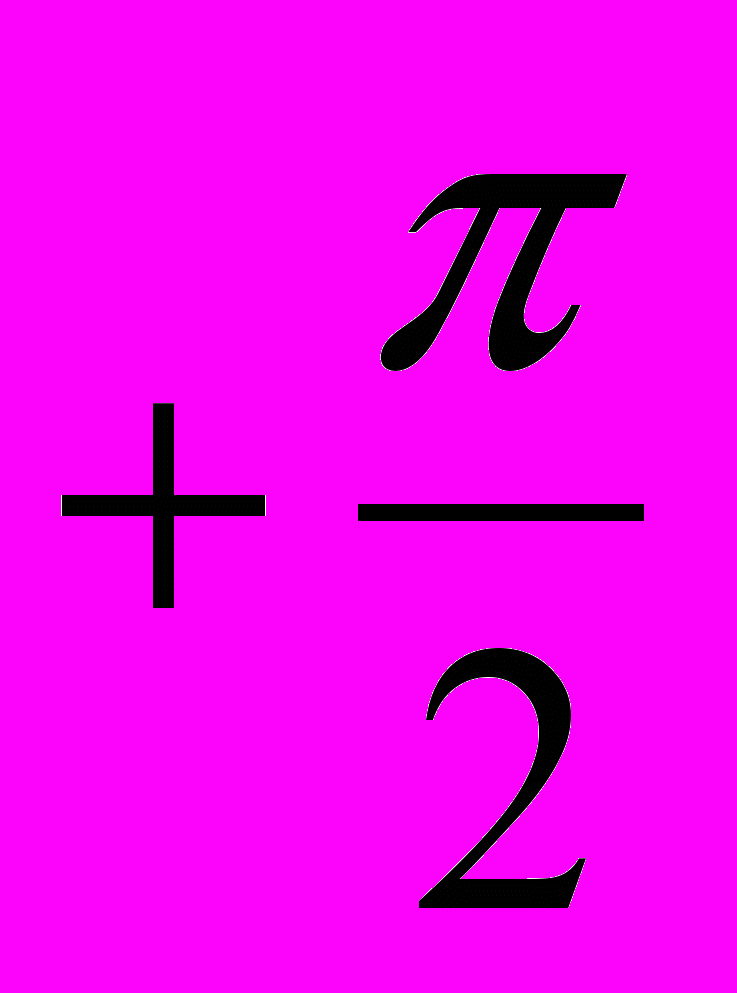Таким образом программа для решения данной задачи может выглядеть, к примеру, так:


var

x, y : real;

alpha : real;

begin

read(x, y);

if x=0 then

if y>0 then alpha:=pi / 2

else if y<0 then alpha:= 3 * pi / 2

else write(‘угол неопределен’) {для точки (0,0) нет полярного угла}

else begin

alpha:=arctan(y/x);

if x<0 then alpha := alpha + pi; {проверим, находится ли угол в левой части координатной плоскости}

if alpha<0 then alpha := alpha + 2 * pi; {обеспечим чтобы найденный угол лежал в интервале (0; 2π)}

end;

end.


Нахождение результата в интервале (0; 2π) не является чем-то обязательным. Здесь скорее требуется, чтобы школьник понимал в принципе в каком диапазоне находятся углы и какой результат получится при сравнении полярных углов точек или (что будет рассмотрено чуть позже) при сортировке множества точек по их полярным углам.

Более того, полярный угол точки (0, 0) для целей каких-то задач можно «для себя» чему-то приравнять (например, нулю), чтобы программа не «спотыкалась».


Векторное произведение векторов

Пусть даны два вектора 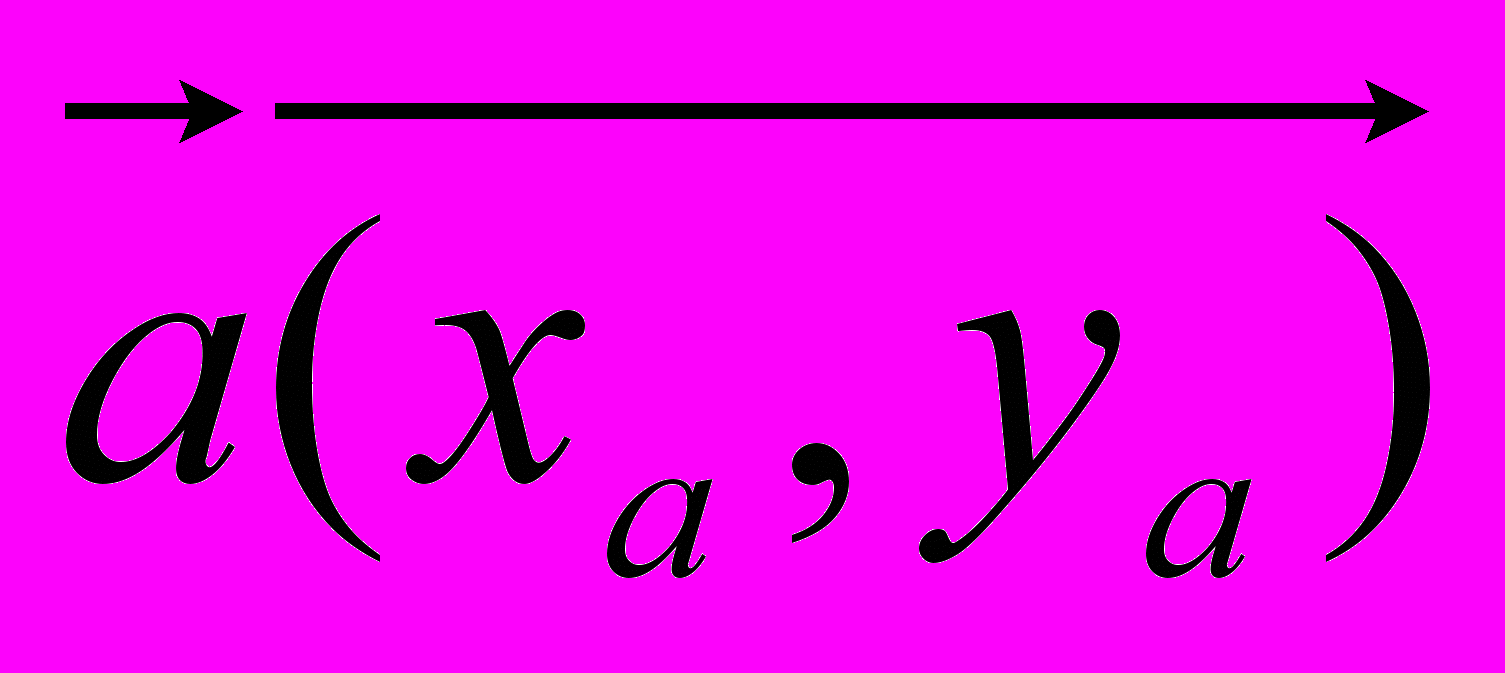и 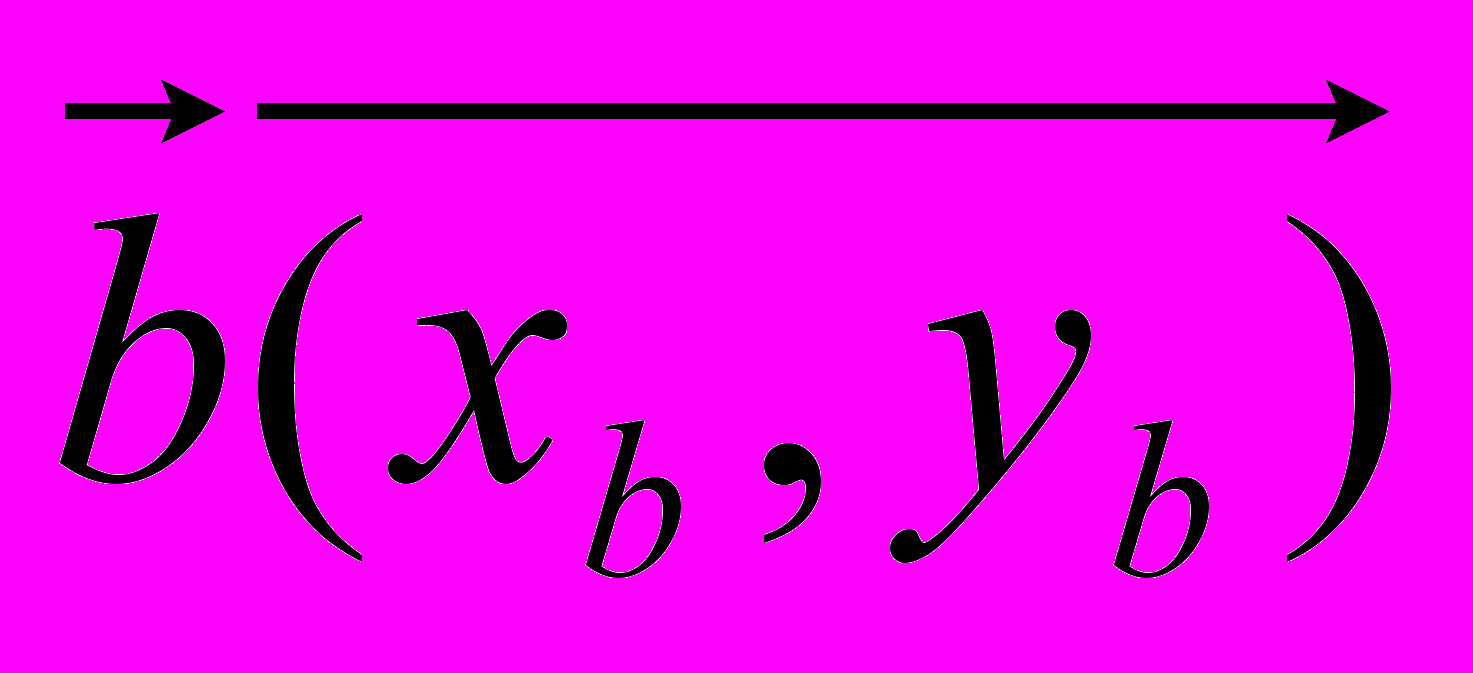. Тогда их векторным произведением будет:

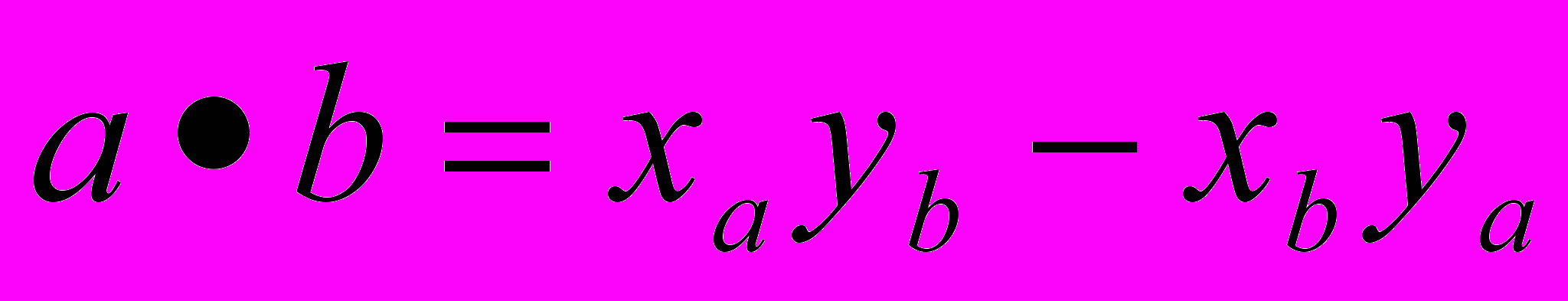. (Строго говоря, векторным произведением двух векторов является вектор указанной длины и перпендикулярный плоскости, в которой лежат исходные вектора, но математических подробностей и без этого достаточно, тем более что школьников интересуют свойства векторного произведения и его применение в решении задач).

По свойству векторного произведения 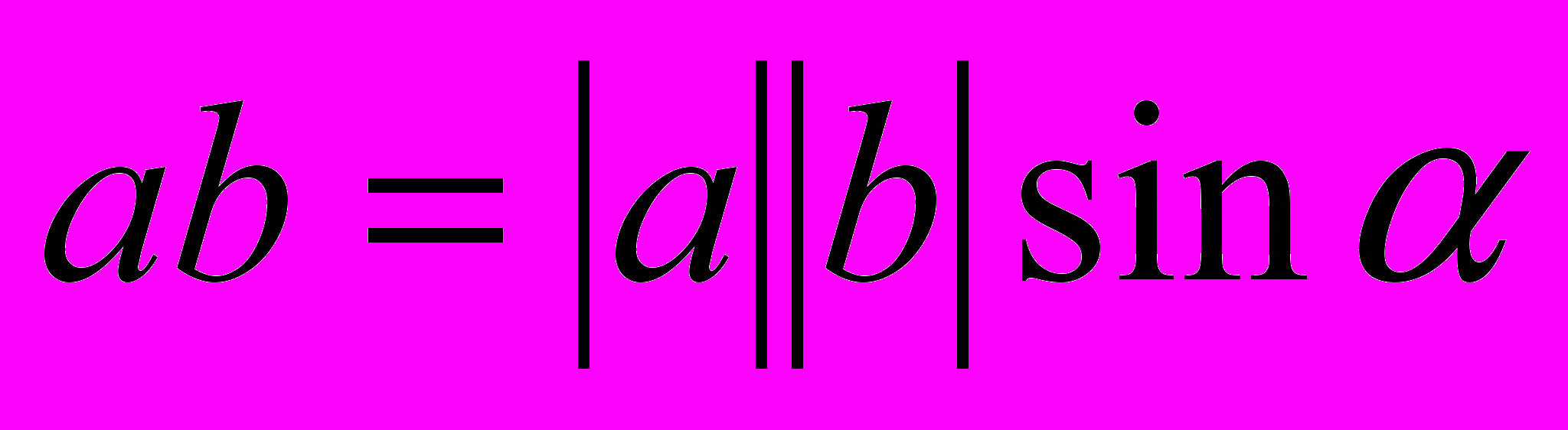, где - длина вектора a, 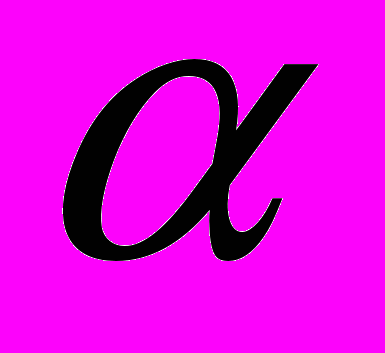- угол между направлениями векторов a и b.

Данное свойство может применяться для:

1. проверки параллельности векторов. Если вектора параллельны, это означает что угол между ними равен нулю, и его синус тоже равен нулю. Следовательно, если векторное произведение равно нулю, то векторы параллельны;
   
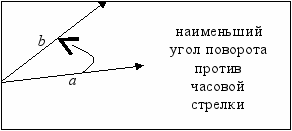
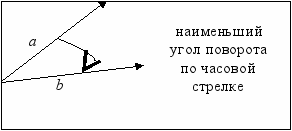
2. для определения наименьшего угла поворота между направлением вектора a и b. Если поворот от a к b делается против часовой стрелки, то векторное произведение положительно, если по часовой стрелке, то отрицательно.
   
   
   

Пример задачи

Пусть некоторый многоугольник задан координатами своих вершин в порядке их обхода (в порядке перечисления по часовой, или против часовой стрелки). Никакие три точки не лежат на одной прямой. Определить, является ли этот многоугольник выпуклым (вывести ответ ДА, если многоугольник выпуклый, и НЕТ – если это не так).

Идея решения данной задачи сводится к следующему. Рассмотрим все пары последовательных сторон многоугольника. Если наименьшие угол поворота везде в одну и ту же сторону, то многоугольник выпуклый. Если где-то встречается ситуация, что направление поворота меняется, то многоугольник не выпуклый (см. иллюстрации).







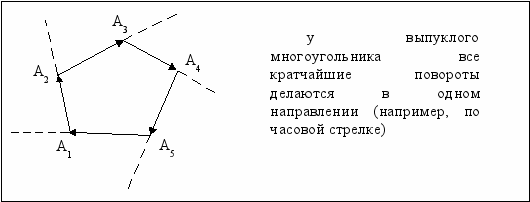
Программа для решения подобной задачи может быть, например, такой:


const

N = 10; { количество точек }

var

Ax : array [1..N+2] of real; {массив X-координат}

Ay : array [1..N+2] of real; {массив Y-координат}

i, p : integer;

x1, y1 : real;

x2, y2 : real;

begin

for i:=1 to N do read(Ax[i], Ay[i]);


Ax[N+1]:=Ax[1]; { искусственно добавим копию первых точек в конец массива, }

Ay[N+1]:=Ay[1]; { чтобы не обрабатывать отдельно пару сторон A_NA₁ и A₁A₂}

Ax[N+2]:=Ax[2];

Ay[N+2]:=Ay[2];


p := 0;

for i:=1 to N do begin

x1:=Ax[i+1] – Ax[i]; { найдем координаты вектора для двух соседних сторон }

y1:=Ay[i+1] – Ay[i];

x2:=Ax[i+2] – Ax[i+1];

y2:=Ay[i+2] – Ay[i+1];

if (x1*y2 - x2*y1)<0 then p:=p+1; {подсчитаем, количество поворотов по часовой стрелке}

end;


if (p=0)or(p=N) then write(‘ДА’) {если все повороты были в одну сторону}

else write(‘НЕТ’);

end.


Последнее сравнение связано с тем, что заранее неизвестно в каком порядке описывались вершины – по часовой или против часовой стрелки.


Вопросы

1. Как изменится последняя программа, если из условия убрать фразу, что «никакие три точки не лежат на одной прямой»?
   
2. Пусть дан набор точек на плоскости. Точки не совпадают. Требуется соединить все эти точки ломанной, у которой не будет самопересечений. Предложите алгоритм решения этой задачи.
   
3. Даны две точки A₁ и A₂. Как можно определить, принадлежит ли точка B прямой A₁A₂?
   
4. *Дан треугольник A₁A₂A₃. Как можно определить, находится ли точка B внутри или снаружи этого треугольника?