Статистика
| Вид материала | Самостоятельная работа |
- Вопросы к зачету по курсу «Финансово-банковская статистика», 27.1kb.
- Прикладная Статистика, 1137.98kb.
- Программа курса Тема I. Предмет, метод и задачи статистики Тема, 1602.61kb.
- Литература по предмету: Тарловская Статистика, 120.71kb.
- 1. Предмет и задачи статистики, 1075.66kb.
- Лекция №1 «Предмет и метод статистики», 80.82kb.
- Нестеров Леонид Иванович, доктор экономических наук, профессор опубликованы следующие, 483.78kb.
- Програма кредитного модуля "Математична статистика" для напрямів підготовки (спеціальностей), 476.21kb.
- 1. Статистичне спостереження, 316.1kb.
- 2. Абсолютні І відносні величини, 314.22kb.
Тема 6. СРЕДНИЕ ВЕЛИЧИНЫ
Средние величины — это обобщающие показатели, характеризующие типичный уровень варьирующего количественного признака в расчете на единицу совокупности в определенных условиях места и времени.
Уровень признака у отдельных единиц совокупности складывается под влиянием разнообразных условий (факторов), одни из которых являются общими для всех единиц, другие — случайными (индивидуальными).
Важнейшее свойство средней заключается в том, что она отражает то общее, что присуще всем единицам исследуемой совокупности. Сущность средней в том и заключается, что в ней взаимопогашаются те отклонения значений признака, которые обусловлены действием случайных факторов, и учитываются изменения, вызванные действием факторов основных. Это позволяет средней отражать типичный уровень признака и абстрагироваться от индивидуальных особенностей, присущих отдельным единицам.
Определить среднюю во многих случаях удобнее через исходное соотношение средней (ИСС) или ее логическую формулу:
ИСС = СУММАРНОЕ ЗНАЧЕНИЕ ИЛИ ОБЪЕМ ОСРЕДНЯЕМОГО ПРИЗНАКА
ЧИСЛО ЕДИНИЦ ИЛИ ОБЪЕМ СОВОКУПНОСТИ
Средняя величина всегда имеет ту же размерность, что и признак у отдельных единиц совокупности.
Объективность и типичность статистической средней могут быть обеспечены лишь при определенных условиях: во-первых, средняя должна вычисляться для качественно однородной совокупности; во-вторых, для исчисления средней должны быть использованы не единичные, а массовые данные, ибо только тогда взаимно погашаются возможные случайные отклонения.
В статистике применяются различные виды средних величин. Выбор вида средней величины и необходимой формулы для ее расчета определяется наличием исходных данных.
1 группа средних величин – степенные средние.
Они объединены общей формулой:
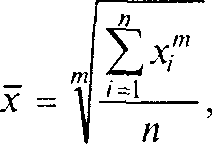
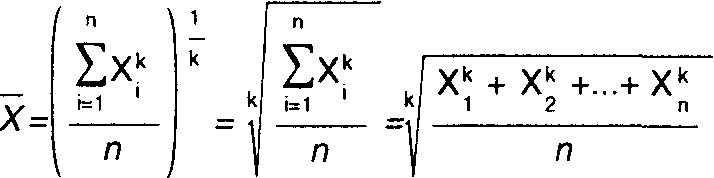
где: х — среднее значение исследуемого явления; т — показатель степени, который определяет вид средней величины; хi — текущее значение осредняемого признака; n — число признаков.
В зависимости от значения показателя степени т различают следующие виды степенных средних величин, если:
т = -1 — средняя гармоническая;
т = 0 — средняя геометрическая;
т = 1 — средняя арифметическая;
Средняя арифметическая (m = 1)
Средняя арифметическая величина представляет собой такое среднее значение признака, при вычислении которого общий объем признака в совокупности сохраняется неизменным. Для того чтобы исчислить среднюю арифметическую, необходимо сумму всех значений признаков разделить на их число.
Она применяется в тех случаях, когда объем варьирующего признака для всей совокупности является суммой значений признаков отдельных ее единиц. Примером средней арифметической может служить общий фонд заработной платы — это сумма заработных плат всех работников.
Средняя арифметическая, вычисленная по не сгруппированным данным, то есть когда значение признака встречается один или одинаковое количество раз называется простой и может быть вычислена по формуле:
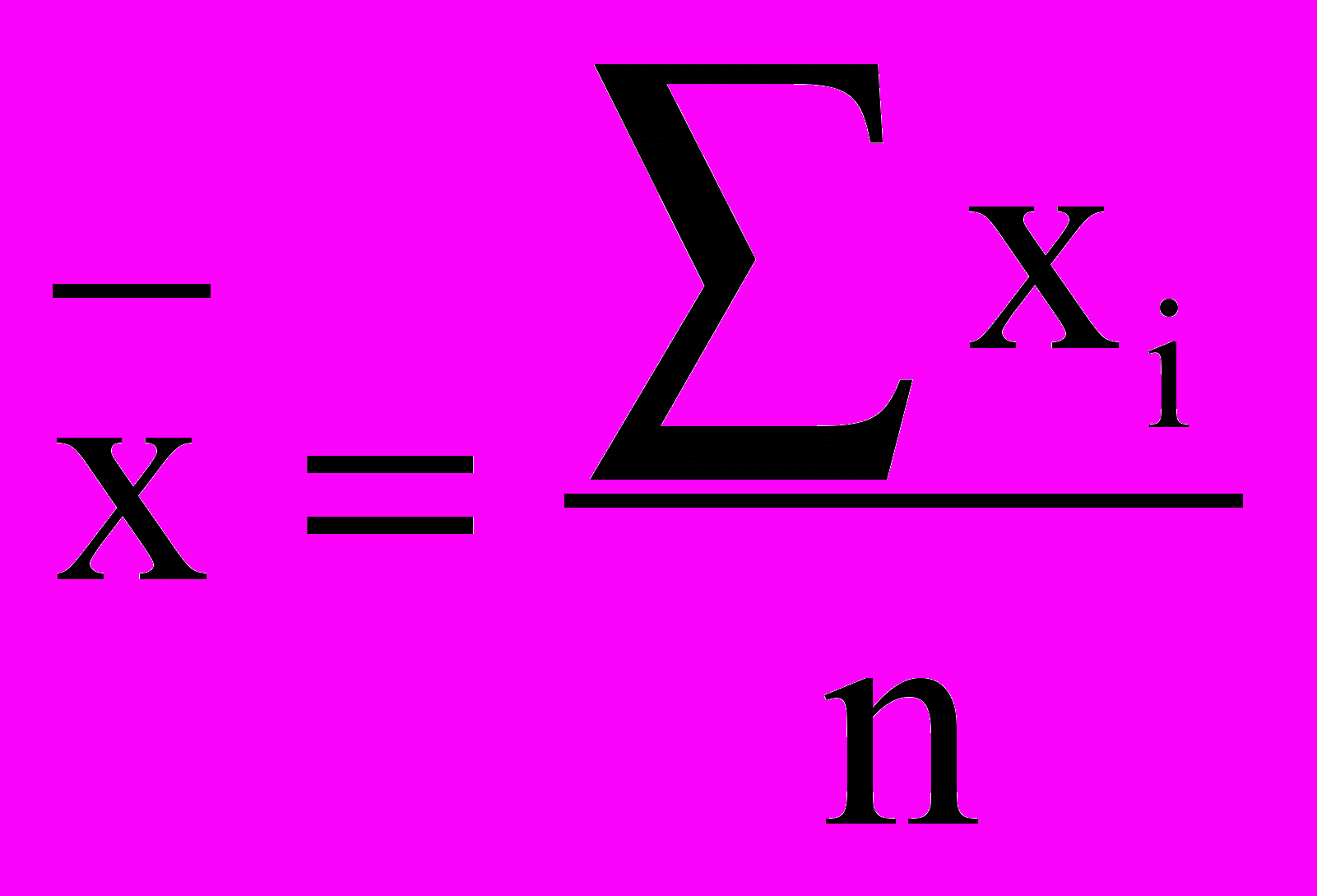
Пример 6.1
Пусть имеются следующие данные о производстве продукта А пятью рабочими бригады за смену:
| Номер рабочего | 1 | 2 | 3 | 4 | 5 |
| Произведено продукции А за смену, шт., хi | 21 | 18 | 20 | 22 | 19 |
Нужно определить среднюю выработку одного рабочего данной бригады. Последняя определяется как средняя арифметическая простая:
_
Х = 21+18+20+22+19 =20 (шт.).
5
Если же отдельные значения признака встречаются по нескольку раз, то в подобных случаях расчет средней производится по, так называемой, средней взвешенной.
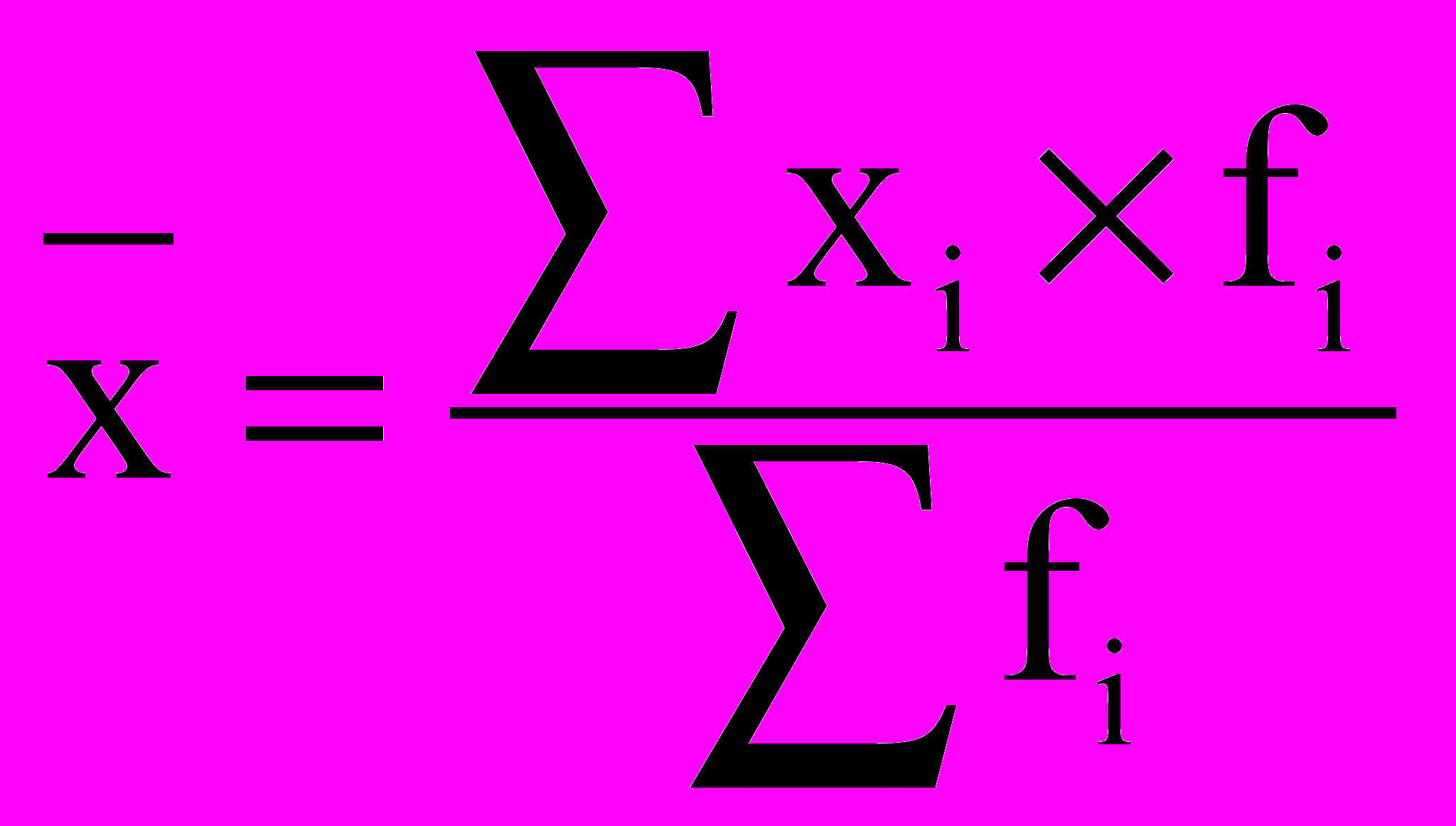
Пример 6.2
(Ряд дискретный)
Имеется следующее распределение 60 рабочих по тарифному разряду:
| Тарифный разряд хi | 2 | 3 | 4 | 5 | 6 |
| Число рабочих fi | 8 | 16 | 17 | 12 | 7 |
Нужно определить средний тарифный разряд рабочих. Расчет производим по средней арифметической взвешенной:
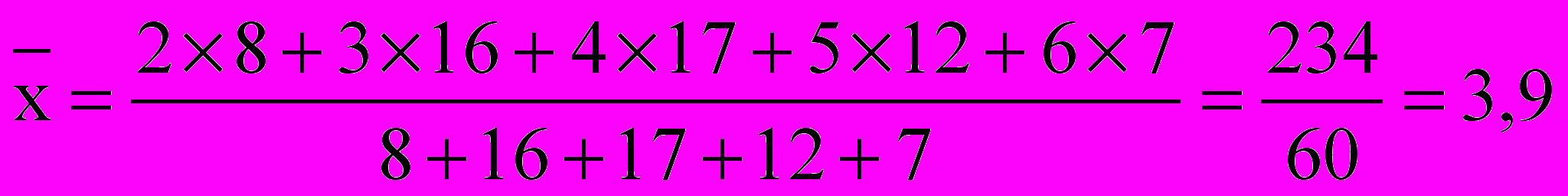
Пример 6.3
(Ряд интервальный)
Для интервальных рядов сначала находят центры (середины) интервалов. Для этого надо найти середину интервала равную полусумме нижней и верхней границы закрытого интервала. За варианту принимается эти значения.
Затем последние умножают на веса, произведения суммируют и делят на сумму весов.
Имеются данные выборочного обследования вкладчиков Сбербанка (табл.4.4).
Определить средний размер вклада.
Таблица 4.4
-
Группы вкладчиков по размеру вклада, руб.
Число вкладчиков fi
Середина интервала хi
хi∙ fi
300- 600
10
450
4500
600-900
20
750
15000
900-1200
50
1050
52500
1200-1500
14
1350
18900
1500-1800
6
1650
9900
Итого
100
-
100800
_
Х = 100800/100 =1008 (руб.).
Средний размер вклада в данной совокупности вкладчиков составил 1008 руб.
Основные свойства средней арифметической.
1. Если индивидуальные значения признака, т. е. варианты, уменьшить или увеличить в к раз, то среднее значение нового признака соответственно уменьшится или увеличится в к раз.
2. Если все варианты осредняемого признака уменьшить или увеличить на число А, то средняя арифметическая соответственно уменьшится или увеличится на это же число.
3. Если вес всех осредняемых вариантов уменьшить или увеличить в к, раз, то средняя арифметическая не изменится.
4. «Нулевое свойство средней». Сумма отклонений отдельных значений признака (вариантов) от средней арифметической равна нулю.
Средняя гармоническая (m=-1)
Допустим теперь, что в нашем распоряжении только данные о сумме вкладов по каждой группе вкладчиков (пример 6.3), т. е. нам известен числитель исходного соотношения, но не известен его знаменатель. Численность вкладчиков по каждой группе можно получить делением суммы вкладов на среднюю сумму вклада. Тогда расчет средней заработной платы в целом будет произведен по формуле средней гармонической взвешенной:
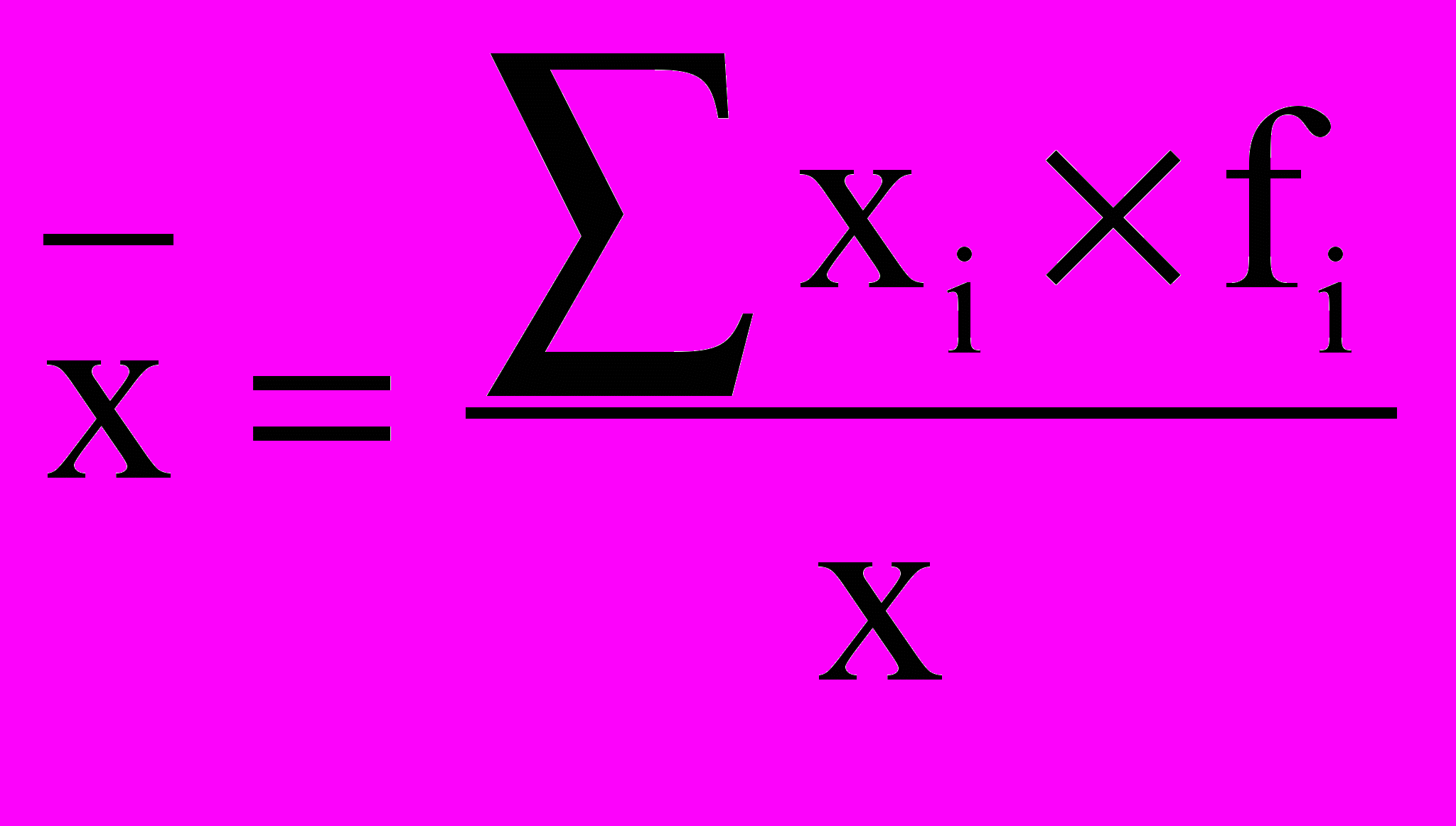
Если данные несгруппированы, расчет производится по средней гармонической простой:
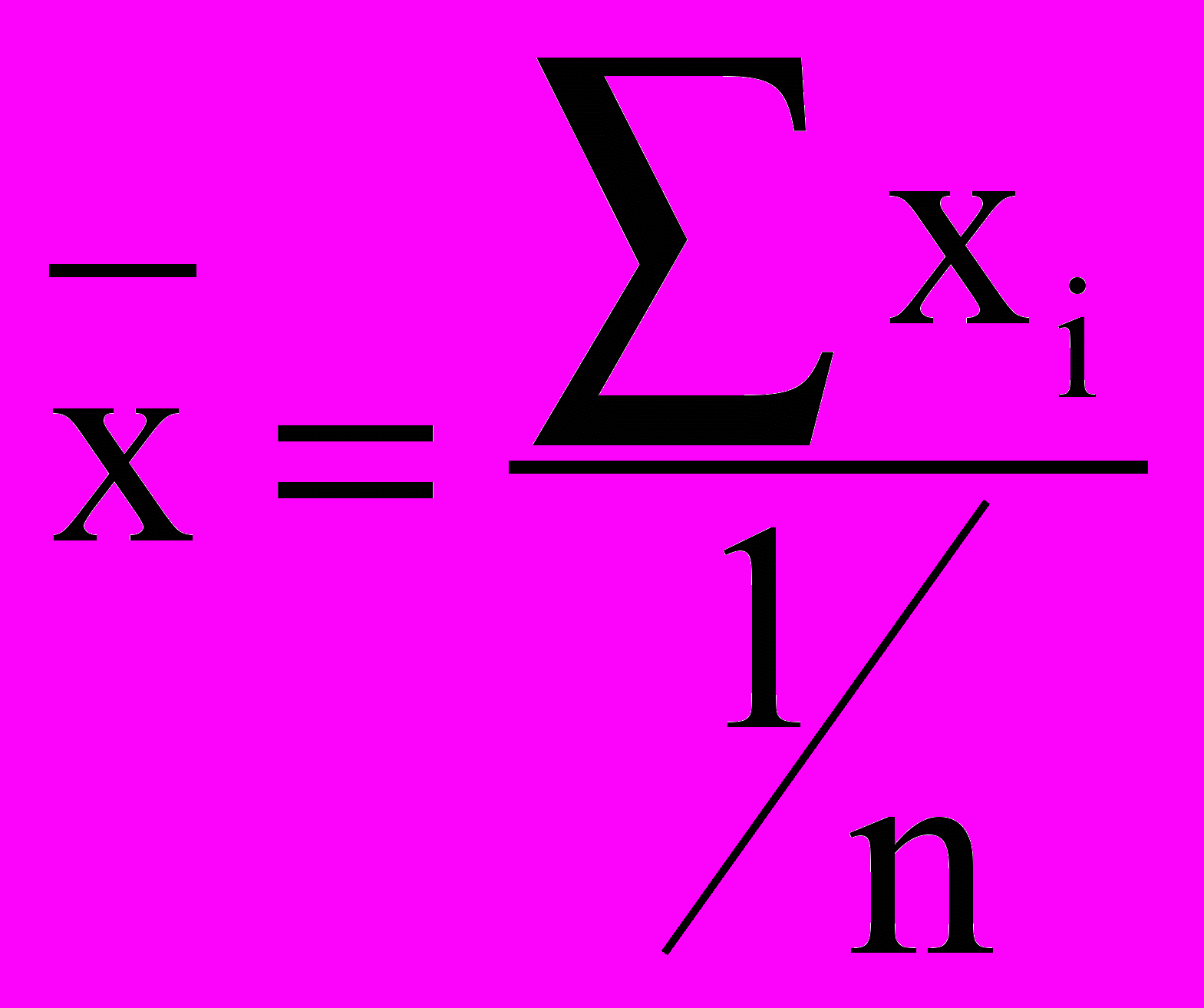
Пример 6.4.
Определить средний размер вклада
-
Группы вкладчиков по размеру вклада, руб.
хi∙ fi
Середина интервала хi
300- 600
4500
450
600-900
15000
750
900-1200
52500
1050
1200-1500
18900
1350
1500-1800
9900
1650
Итого
100800
-
_
Х=(4500/450)+(1500/750)+(52500/1050)+(18900/1350)+(9900/1650)=1008 руб.
В примерах 6.3. и 6.4. мы использовали разные формы средних, но получили один и тот же ответ. Это обусловлено тем, что для конкретных данных каждый раз реализовывалось одно и то же исходное соотношение средней.
Средняя геометрическая (m=0)
Средняя геометрическая простая применяется в тех случаях, когда индивидуальные значения признака представляют собой относительные величины динамики, построенные в виде цепных величин, как отношение к предыдущему уровню каждого уровня в ряду динамики, т. е. характеризует средний коэффициент роста.
Она исчисляется извлечением корня степени n из произведений отдельных значений — вариантов признака по формуле:
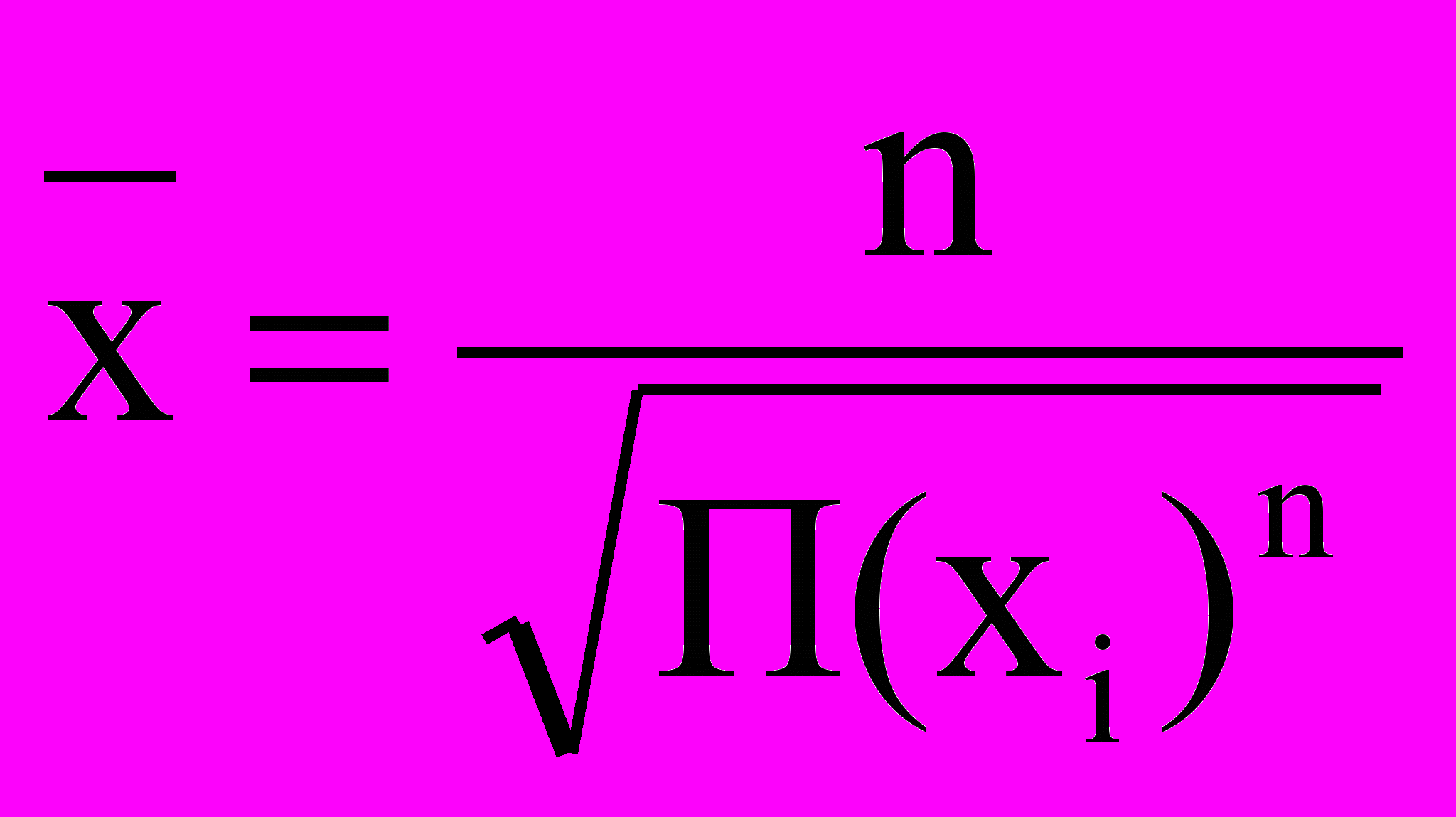
где П — оператор умножения, знак произведения; n — число вариантов.
2 группа средних величин – структурные средние.
Для расчета степенных средних, как уже было показано выше, в большинстве случаев необходимо располагать данными не только о вариантах значений признака в исследуемой совокупности, но и о весомости отдельных вариантов значений.
Поэтому при условии недостаточности исходных данных, которая в ряде случаев объективно может возникать при сборе информации (например, ограничения в связи с так называемой «коммерческой тайной»), предпочтение отдается структурным, или позиционным, средним — медиане и моде. Мода и медиана определяются лишь структурой распределения. Поэтому их именуют структурными позиционными средними и часто используют как среднюю характеристику в тех совокупностях, где расчет средней степенной невозможен или нецелесообразен.
Мода — значение признака, которое имеет наибольшую частоту в статистическом ряду распределения.
Отыскание моды производится по-разному, и это зависит от того, представлен ли варьирующий признак в виде дискретного или интервального ряда. Поиск моды в дискретном ряду:
В столбце частот находится наибольшее число, характеризующее наибольшую частоту. Ей соответствует определенное значение признака, которое и является модой.
В интервальном вариационном ряду сначала определяется модальный интервал. Это интервал с наибольшей частотой. Затем значение моды вычисляется по формуле:
( fмо – fмо--1 )
Мо = хн + h х ( fмо – fмо--1 ) + ( fмо – fмо+1 )
где: хн — нижняя граница модального интервала; h - величина модального интервала; fмо – частота модального интервала; fмо--1 – частота предыдущего интервала; fмо+1 – частота последующего за модальным интервала
:
Мода широко используется в статистической практике при изучении, например, покупательного спроса, регистрации цен и т. д.
Медиана – это такое значение признака, которое делит ранжированный ряд распределения на две равные (по числу единиц части - со значениями признака меньше медианы и со значениями признака больше медианы). Для того чтобы найти медиану, нужно отыскать значение признака, которое находится на середине упорядоченного ряда то есть к отысканию порядкового номера медианы.
∑ fi
NМе = 2
Затем, если по накопленным частотам определяется либо сама медиана (для дискретных рядов) – это значение, на которое приходится единица с соответствующим NМе.
Ме = равна этому значению.
Либо медианный интервал (для интервальных рядов) – это интервал, который содержит NМе. Затем медиана рассчитывается по формуле:
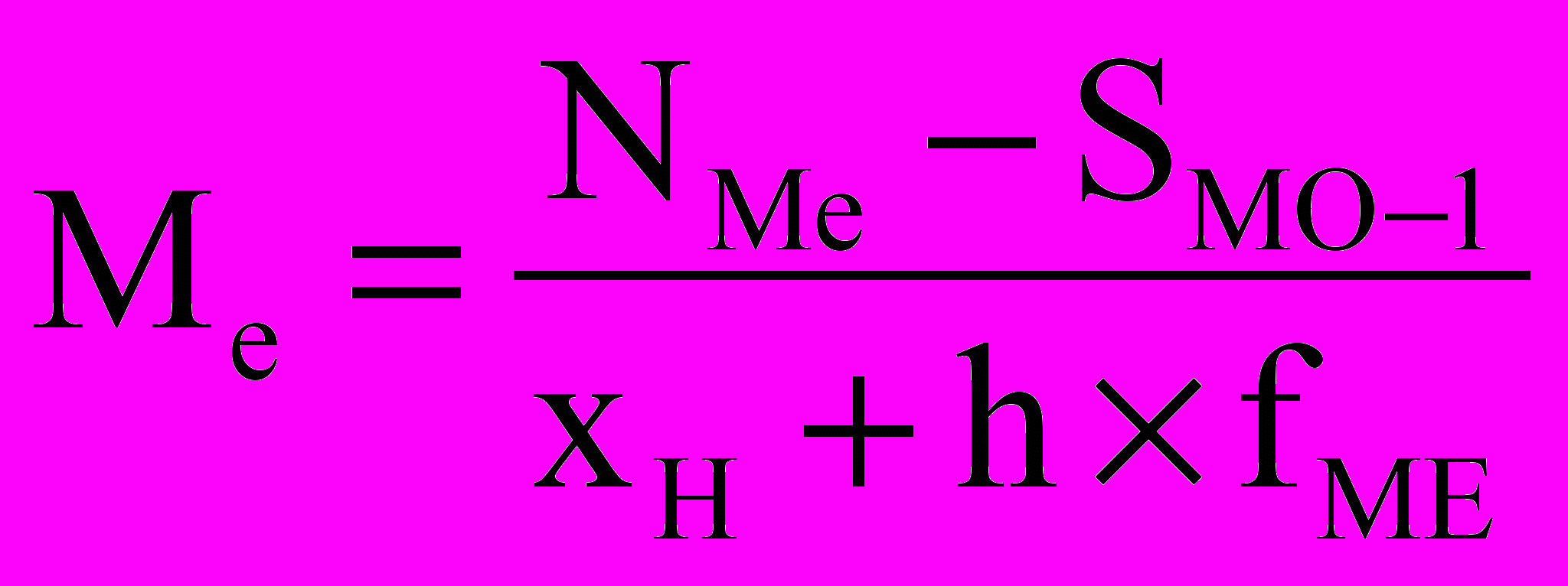
где: хн — нижняя граница медианного интервала; h — медианный интервал; NМе — номер медианы; S мо--1 — сумма частот, накопленных до начала медианного интервала; fме — частота медианного интервала.
Пример 6.5.
Воспользуемся таблицей из примера 6.2.
Имеется следующее распределение 60 рабочих по тарифному разряду. Найти моду и медиану.
| Тарифный разряд хi | 2 | 3 | 4 | 5 | 6 | Итого |
| Число рабочих fi | 8 | 16 | 17 | 12 | 7 | 60 |
| Накопленная частота Fi | 8 | 24 | 41 | 53 | 60 | - |
1) Максимальная частота f =17, соответствует значению признака х = 4, следовательно, Мо=4.
2) 60/NМе = 2 = 30 Единица с номером 30 приходится на х=4, следовательно, Ме = 4.
(Обратите внимание на то, что значение структурных средних близко к значению средней арифметической 3,9, что подтверждает их правильность)
Пример 6.6. (ряд интервальный)
По данным примера 6.3. определим моду и медиан.
| Группы вкладчиков по размеру вклада, руб. | Число вкладчиков fi | Середина интервала хi | Накопленная частота Fi |
| 300- 600 | 10 | 450 | 10 |
| 600-900 | 20 | 750 | 30 |
| 900-1200 | 50 | 1050 | 80 |
| 1200-1500 | 14 | 1350 | 94 |
| 1500-1800 | 6 | 1650 | 100 |
| Итого | 100 | - | - |
1) Максимальная частота f = 50 модальный интервал (900 - 1200)
. 50 – 20 .
Мо = 900 + 300 • (50 – 20) + (50-14) = 1036,4 руб.
100
2)NМе = 2 = 50, по накопленной частоте определяем медианный интервал, то есть интервал, в который попадает единица совокупности с данным номером – это интервал (900-1200).
. 50 – 30 .
Ме = 900 + 300 • 50 = 1020 руб.
Вывод: Наиболее часто в данной совокупности встречается вклад размером 1036,4 руб. Одна половина вкладчиков имеет вклад до 1020 руб., а другая свыше 1020 руб.
КОНТРОЛЬНЫЕ ВОПРОСЫ
6.1. Что такое средняя величина?
6.2. Как вычисляются простая и взвешенная средняя арифметическая
6.3. Как находится средняя арифметическая для интервального ряда?
6.4. Какие показатели относятся к структурным средним?
6.5. Какой показатель называется модой ? Как она находится?
6.6. Что характеризует медиана, как она вычисляется?
