Курс лекций по начертательной геометрии (часть 3). Задание геометрических образов на чертеже

Вид материала

Курс лекций

Содержание Линия пересечения двух поверхностей определяется как геометрическое место точек, полученных в результате пересечения горизонтале К неизвестна, то сначала находим натуральную величину того отрезка перпендикуляра, отметки которого 6 АВС. Для этого проградуируем отрезок АВ АВС, повернутого в плоскости П S в исходной проекции плоскости. Проводим через S

Подобный материал:

• Краткий курс лекций, 182.24kb.
• Наименование и краткое содержание лекций № лек. Тема лекции, краткое содержание Количество, 72.86kb.
• Задание по начертательной геометрии для студентов 1 курса   Задание №1 Задача №1 , 909.02kb.
• Задание геометрического образа на комплексном чертеже посредством определителя. Задание, 32.56kb.
• Язык описания алгоритмов начертательной геометрии adgl, 70.57kb.
• Темы лекций по начертательной геометрии для студентов очной формы обучения 1 курс, 26.7kb.
• Задание точки на чертеже в системе двух- трех плоскостей проекций. Линии связи. Задание, 503.91kb.
• Рабочая программа по геометрии 10 класс, 149.49kb.
• Рабочая программа по геометрии 10 класс, 109.38kb.
• Программа-минимум кандидатского экзамена по специальности 05. 01. 01 «Инженерная геометрия, 88.49kb.

Тимофеева Т.В.

Курс лекций по начертательной геометрии (часть 3).

ЗАДАНИЕ ГЕОМЕТРИЧЕСКИХ ОБРАЗОВ НА ЧЕРТЕЖЕ

С ЧИСЛОВЫМИ ОТМЕТКАМИ

Задание поверхностей


В начертательной геометрии принимается кинематический способ образования поверхностей, т.е. поверхность рассматривается как геометрический образ, полученный непрерывным движением линии, перемещающейся в пространстве по определенному закону (в отличие от математики, где поверхность – геометрический образ, имеющий определенную закономерность, выражаемую уравнением). Линия, которая при своем перемещении образует поверхность, называется образующей. Закон перемещения образующей в пространстве – закон образования поверхности.

На проекциях с числовыми отметками поверхности задают проекциями характерных точек или каркасом линий (чаще всего горизонталей), а также определителем.

Определитель – совокупность всех независимых геометрических условий, однозначно определяющих все множество точек данного геометрического образа на комплексном чертеже.

По форме образующей поверхности делятся на линейчатые (образующая – прямая линия), циклическая (образующая – окружность), поверхности общего вида (образующая – плоская или пространственная кривая). Среди линейчатых поверхностей рассмотрим многогранники (пирамида и призма), а также конус и цилиндр.

Многогранники удобно задавать проекциями вершин:

Пирамида Σ(А,В,С, S).

Призма Δ(A,B,C,D,E,F).



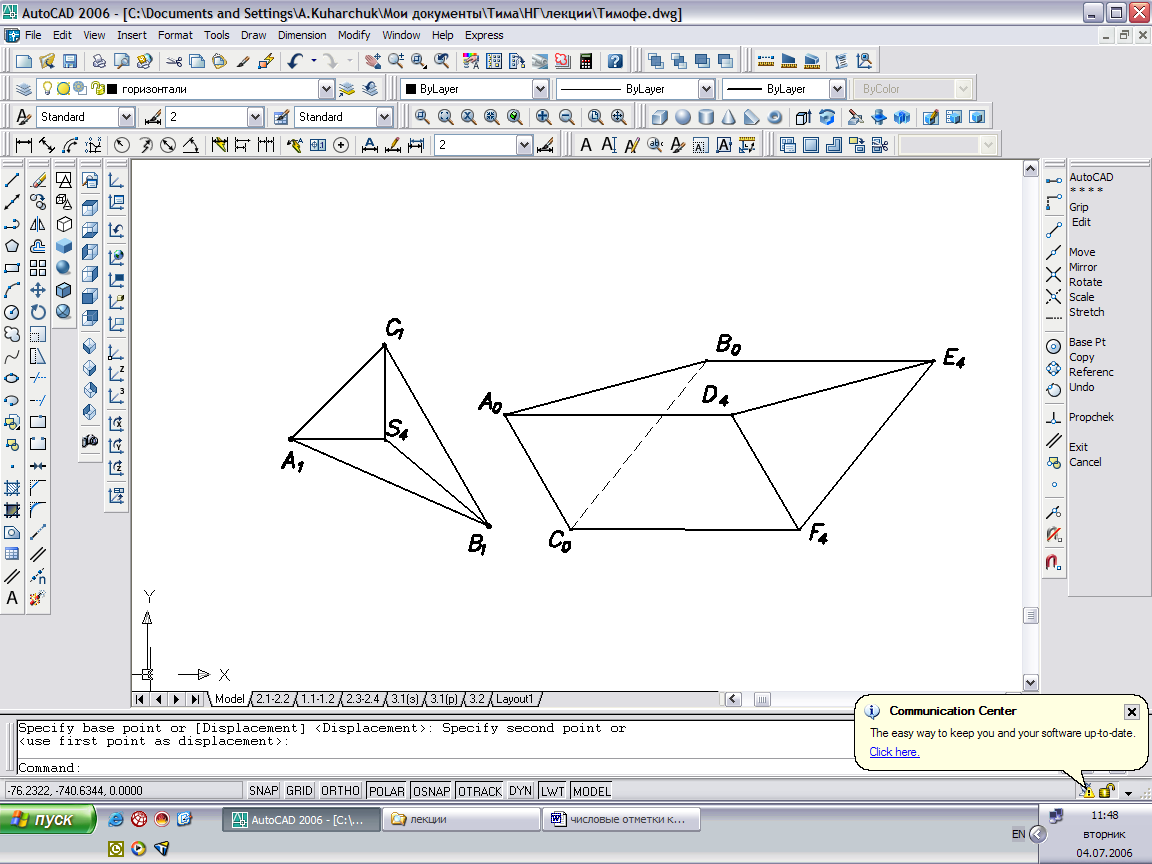
Рис.37


Или определителем:

Призма Δ(A,B,C, СD). Закон образования поверхности: l ׀׀ CD, l x ABC.




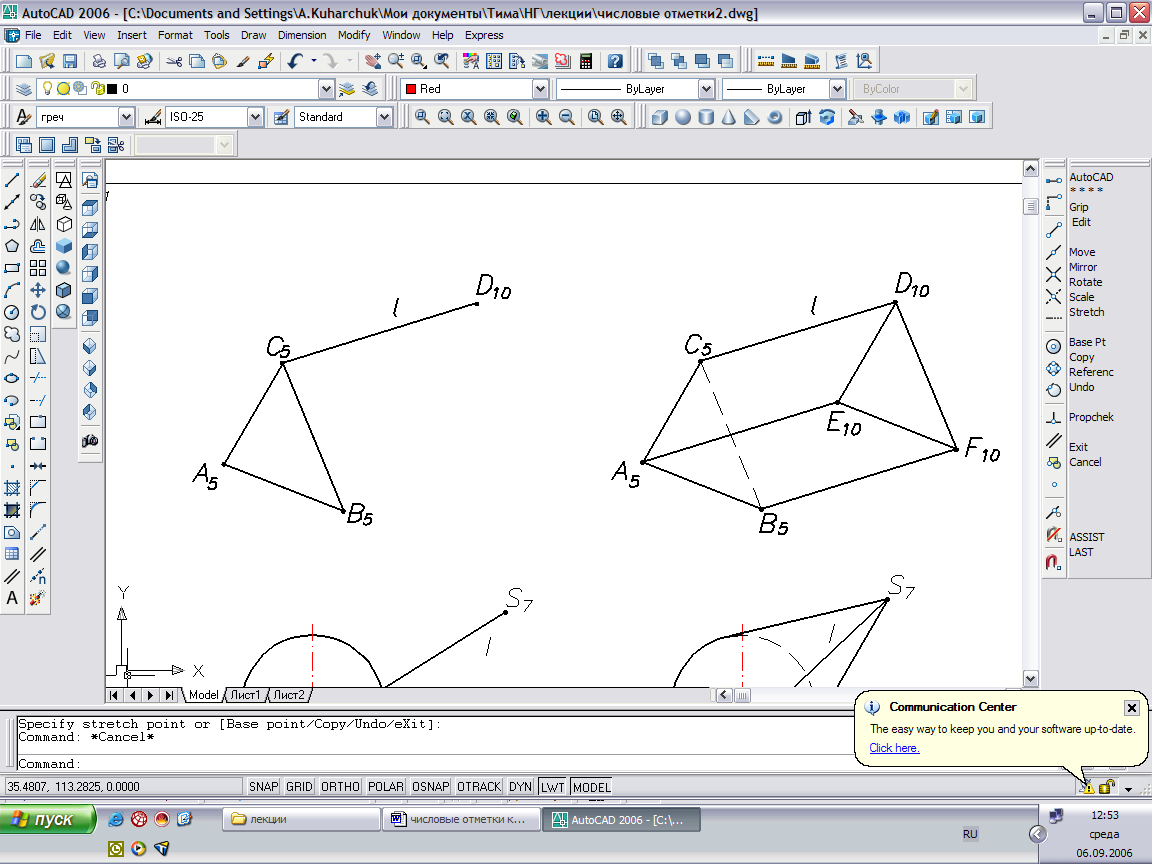
Рис.38


Конус и цилиндр (прямые или наклонные) также часто задают определителем:

Конус Σ(h₀, S). Закон образования поверхности: l э S, l x h₀.





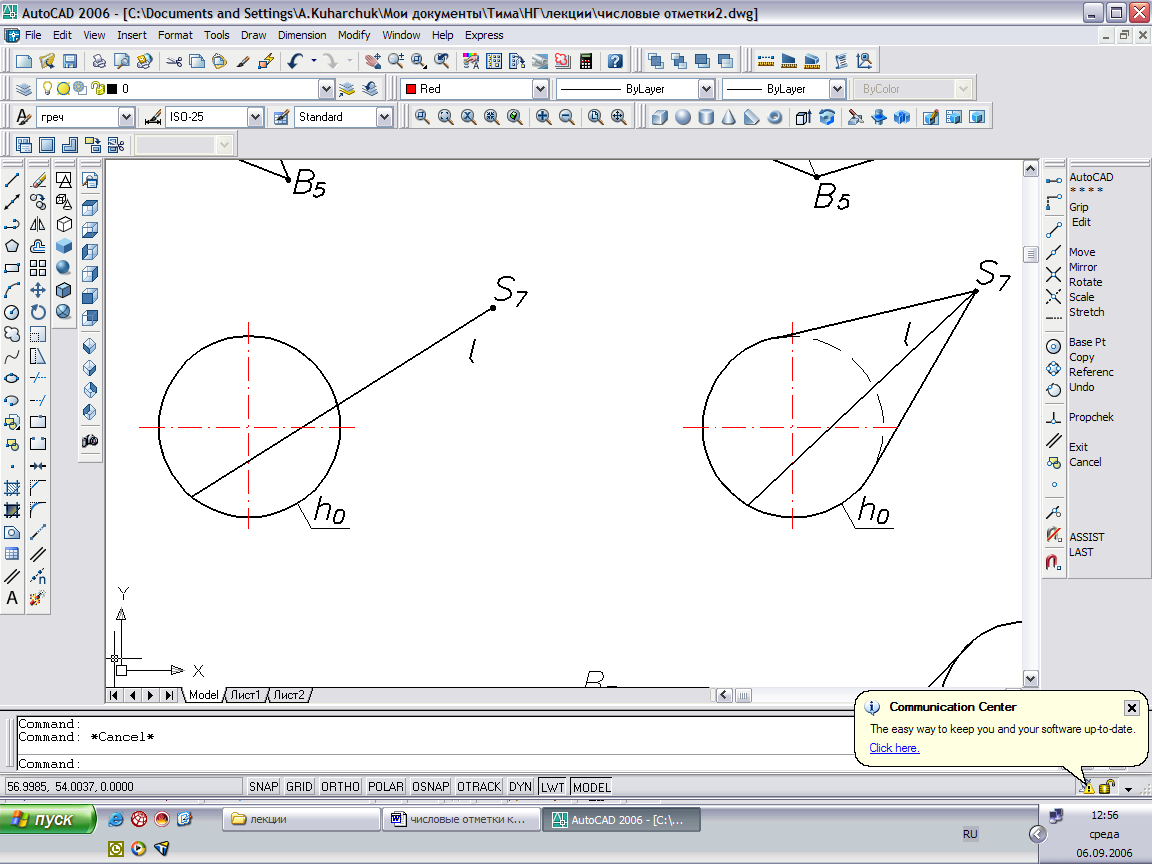
Рис.39


Цилиндр Δ(h₃, АВ). Закон образования поверхности: l ׀׀ AB, l x h₃.



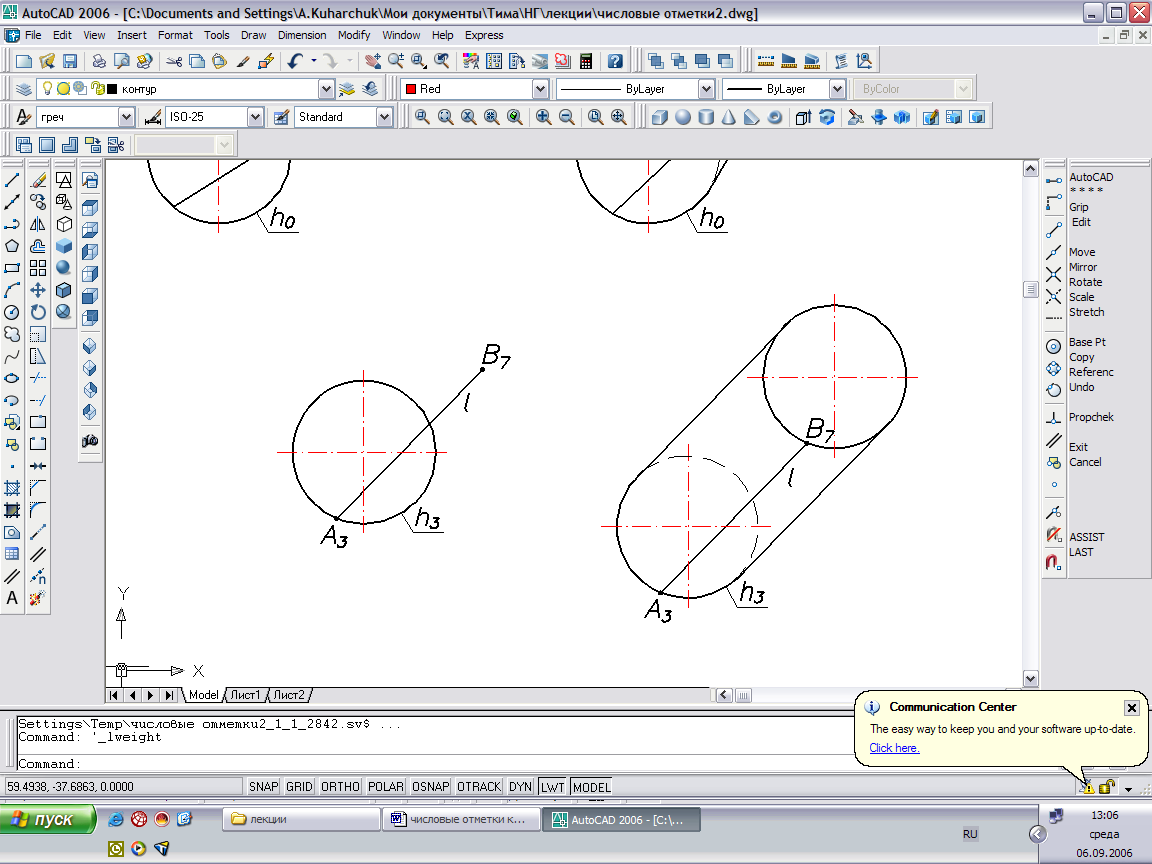
Рис.40


Любую поверхности на чертеже с числовыми отметками можно задать каркасом горизонталей.



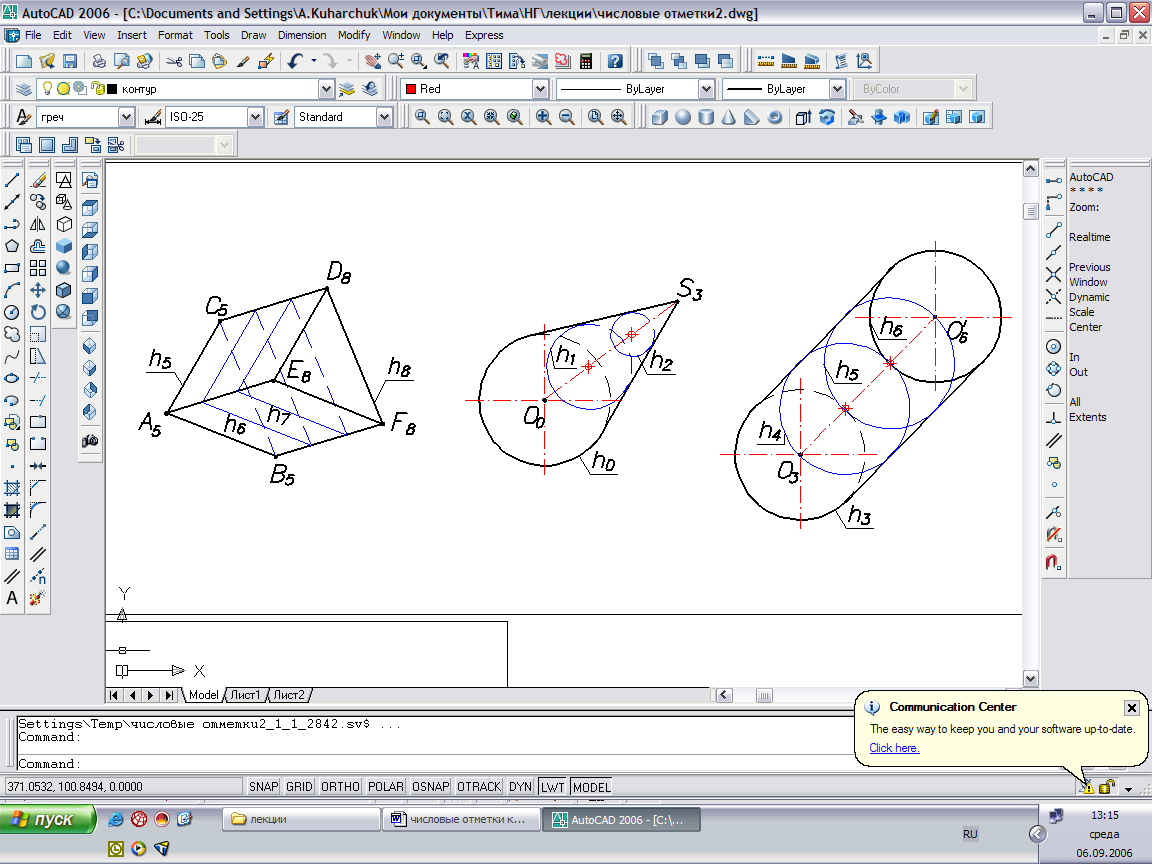
Рис.41

Топографическая поверхность - поверхность некоторого участка земли. Образование такой поверхности не подчинено никакому геометрическому закону. Горизонтали топографической поверхности располагаются на чертеже с шагом 1, 10, 50 или 100 м. По отметкам горизонталей можно судить о форме изображений на плане (карте) местности. Для обозначения ската поверхности используются бергштрихи, которые направляют к нижней горизонтали. На вершине бергштрихи ставятся на одной из верхних горизонталей в сторону ската воды. В котловине бергштрихи направлены внутрь нижней горизонтали.



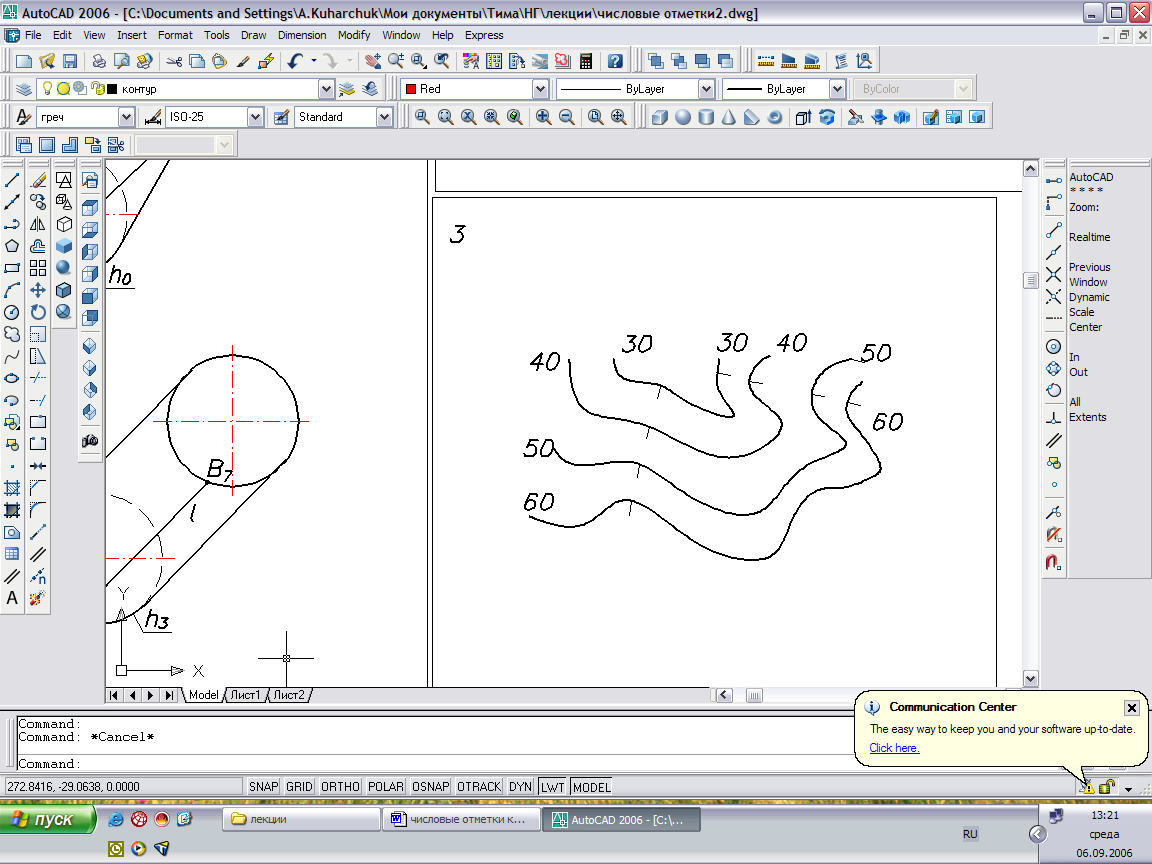
Рис.42

Поверхность одинакового ската – поверхность, которая образуется при отсыпке откосов от кривой линии, меняющейся по высоте – огибающая семейства прямых круговых конусов с вертикальными осями. Такое семейство образует в пространстве конус, вершина которого перемещается по заданной пространственной кривой, а ось при движении сохраняет вертикальное положение. Горизонталями поверхности одинакового ската будут эквидистантные кривые - кривые, находящиеся друг от друга на равном расстоянии.



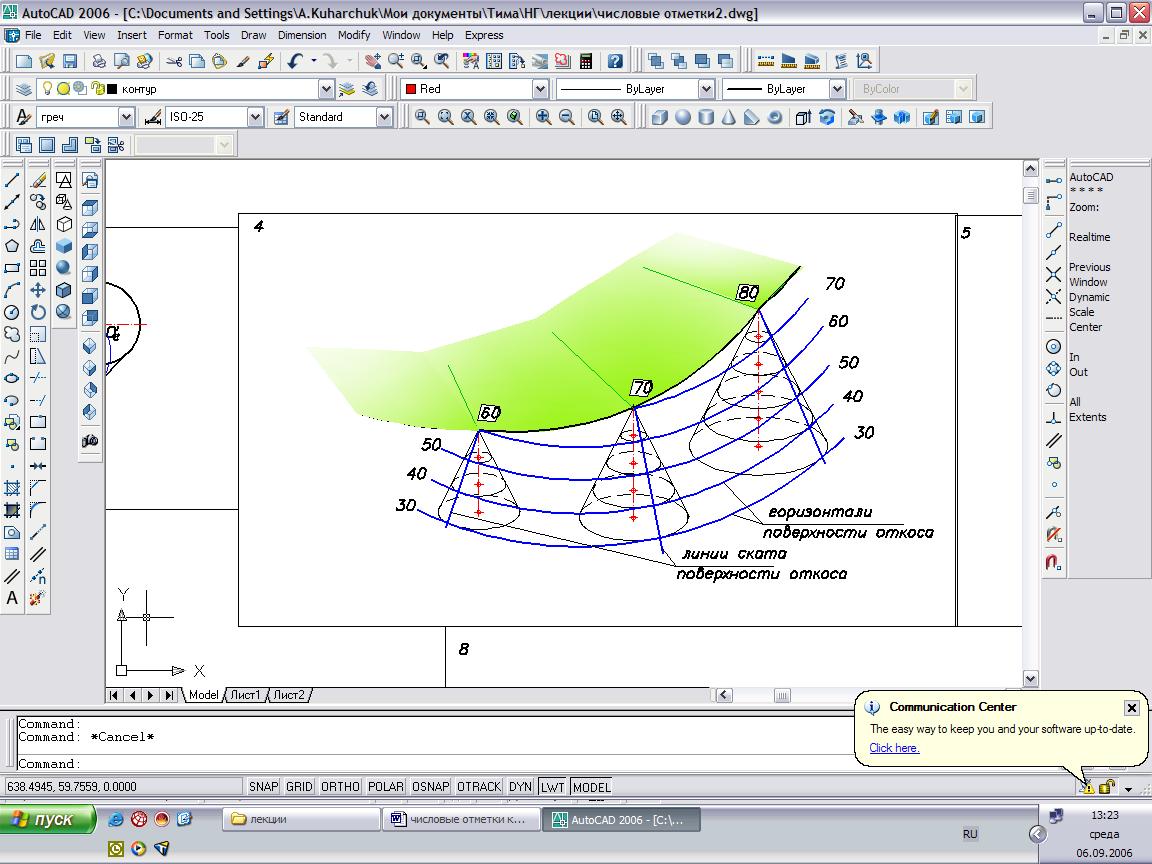
Рис.43


Пример: Построить каркас горизонталей поверхности одинакового ската, проходящей через данную линию. Уклон поверхности 1:1.



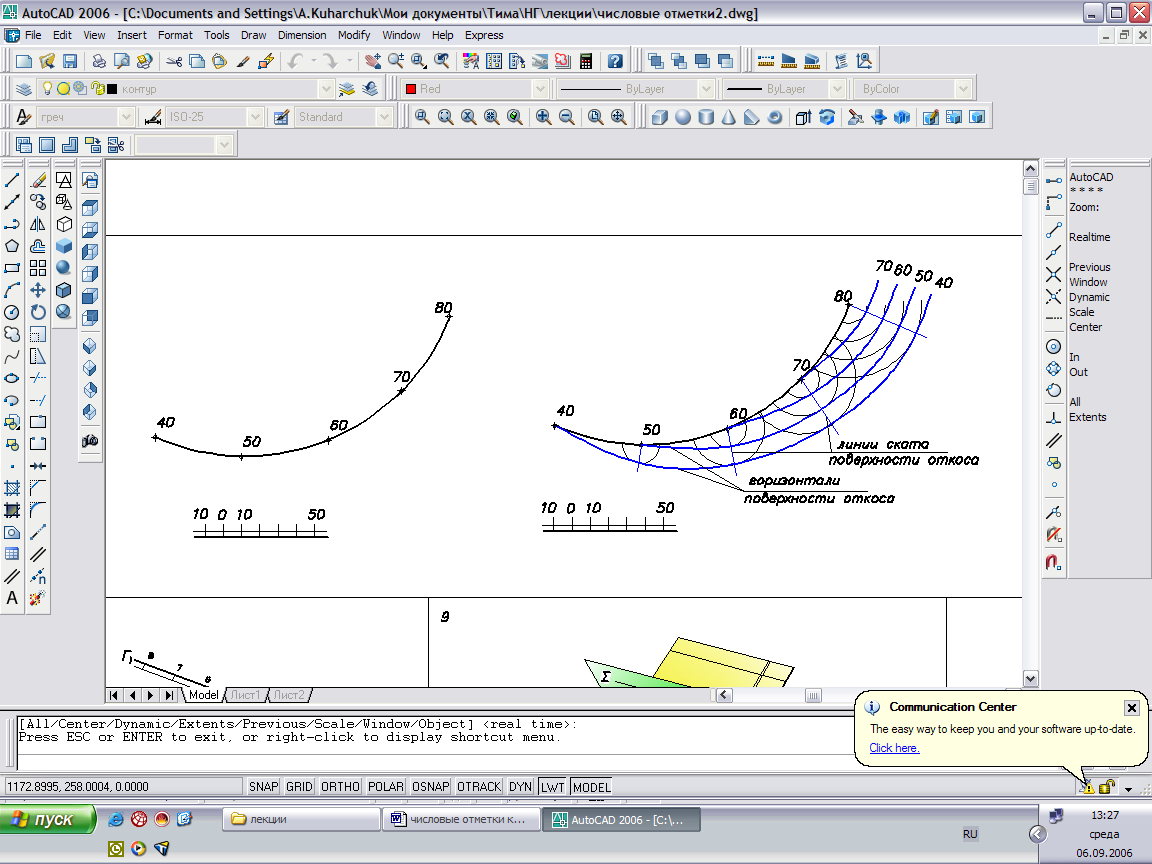
Рис.44

Позиционные задачи



Позиционными называются задачи, в которых рассматривается взаимное расположение геометрических образов друг относительно друга. К позиционным задачам относятся задачи на принадлежность геометрических образов друг другу и задачи на пересечение геометрических образов. Задачами на принадлежность являются задачи на построение проекций: точек на линии или поверхности, линий на поверхности, линий и поверхностей, проходящих через заданные точки и линии. Среди позиционных задач на пересечение можно выделить две главные:

1 ГПЗ (первая главная позиционная задача) – пересечение линии и поверхности;

2 ГПЗ (вторая главная позиционная задача) – пересечение поверхностей.


Решение 2 ГПЗ (пересечение поверхностей)


Нахождение линии пересечения двух поверхностей основано на применеии способа секущих плоскостей. Общая линия двух поверхностей - линия пересечения - состоит из точек пересечения линий этих поверхностей, лежащих в одной плоскости (вспомогательной плоскости – плоскости-посреднике). В качестве таких плоскостей-посредников удобно использовать горизонтальные плоскости, т.к. семейство горизонтальных плоскостей-посредников рассечет любую поверхность по семейству горизонталей этой поверхности.

^ Линия пересечения двух поверхностей определяется как геометрическое место точек, полученных в результате пересечения горизонталей с одинаковыми числовыми отметками.

Горизонтали h^׀ и h^׀׀ с одинаковыми отметками являются линиями, по которым некоторая горизонтальная плоскость уровня Λ пересекает соответственно поверхности Г ^І и Г ^ІІ. Точка М пересечения горизонталей принадлежит искомой линии пересечения этих поверхностей.

Задача с помощью символов записывается в следующем виде: найти Г ^I х Г ^II = m (K, M, N...).

Алгоритм решения:

1. Для решения задачи вводим вспомогательную плоскость-посредник общего положения Λ.
   
2. Находим линии пересечения плоскости-посредника с каждой из плоскостей: Λ x Г ^I = h ^I, Λ х Г ^II = h ^II.
   

3. Точка пересечения этих линий – общая для двух плоскостей: h ^I x h ^II = M. Через эту точку пройдет искомая линия пересечения поверхностей Г ^I и Г ^II.



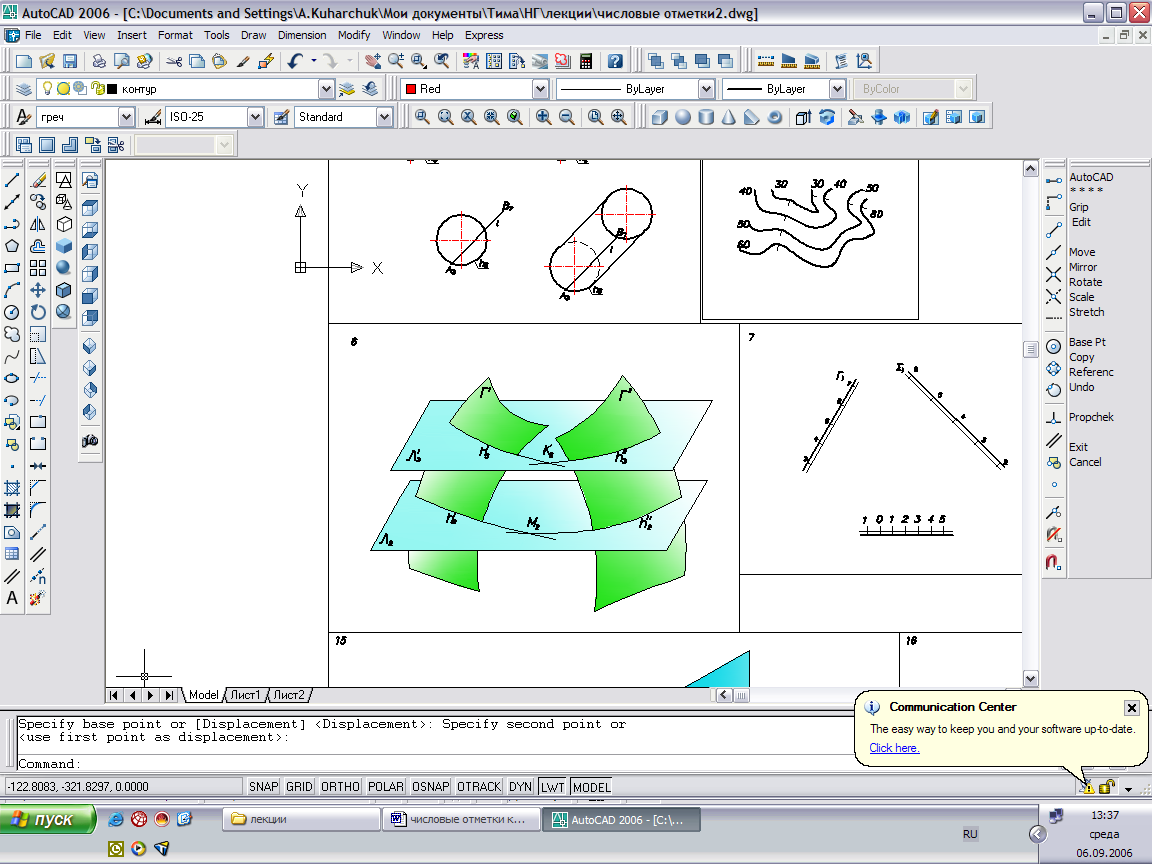
Рис.45

Пример: Определить линию пересечения двух плоскостей Г и Σ.





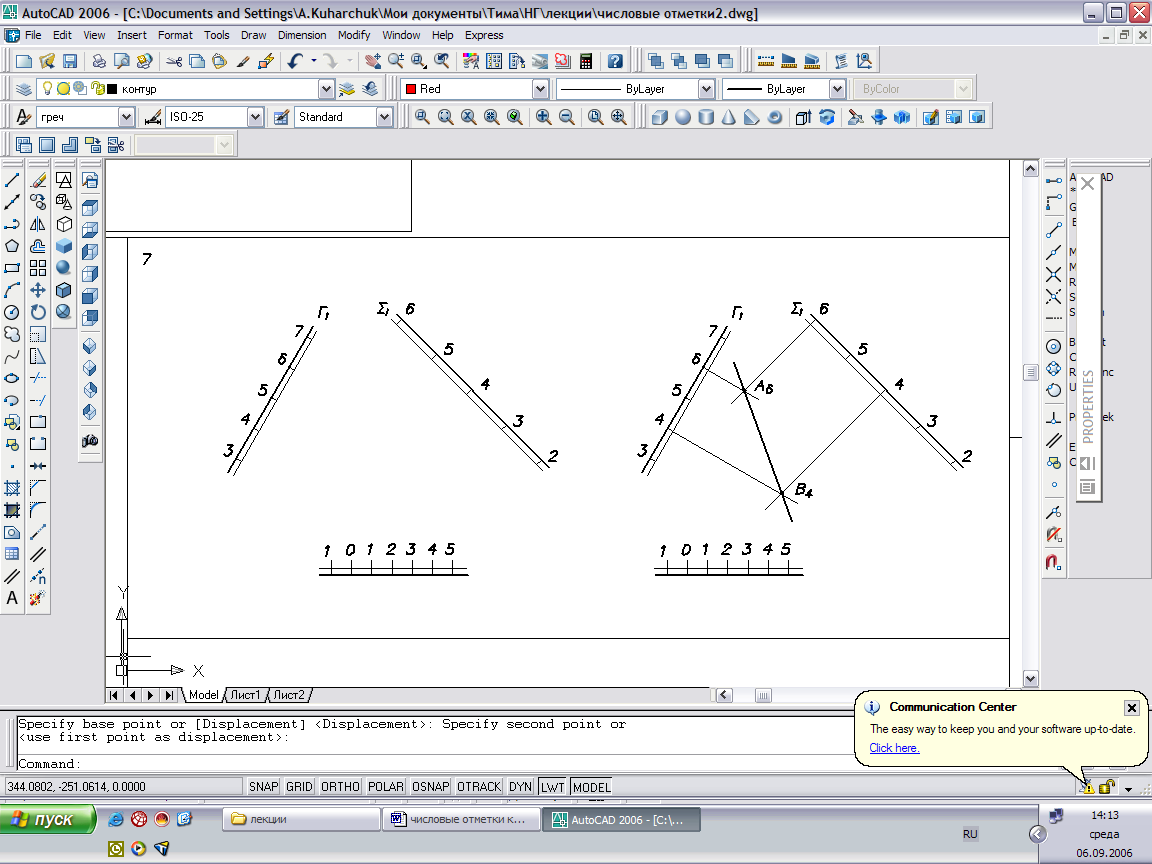
Рис.46


Для построения линии пересечения (прямой) двух плоскостей определяют точки пересечения двух пар горизонталей с любыми одинаковыми отметками. Прямая АВ является искомой.

Частный случай 1: Углы падения двух плоскостей одинаковы (следовательно – интервалы плоскостей равны).



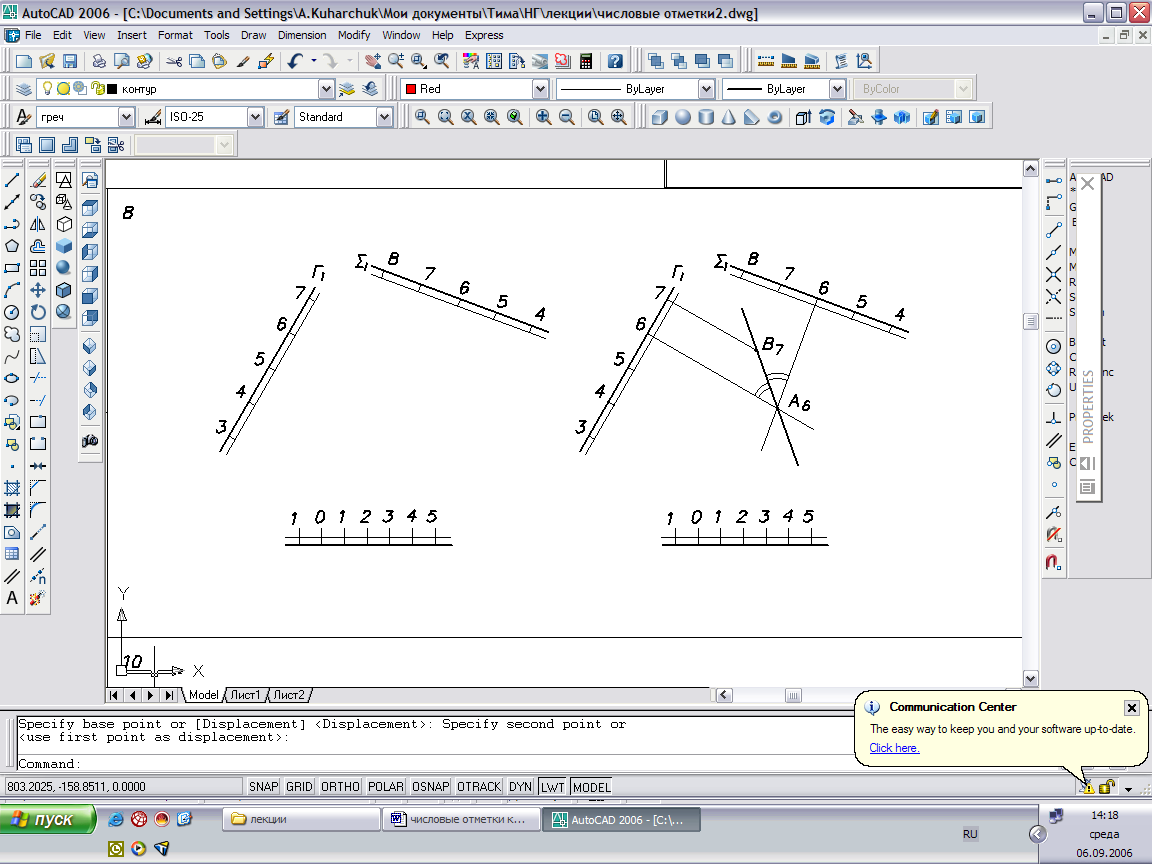
Рис.47


Линия пересечения – биссектриса угла, образованного проекциями горизонталей данных плоскостей.


Частный случай 2: Масштабы падения двух плоскостей Λ и Δ параллельны,

интервалы не равны.





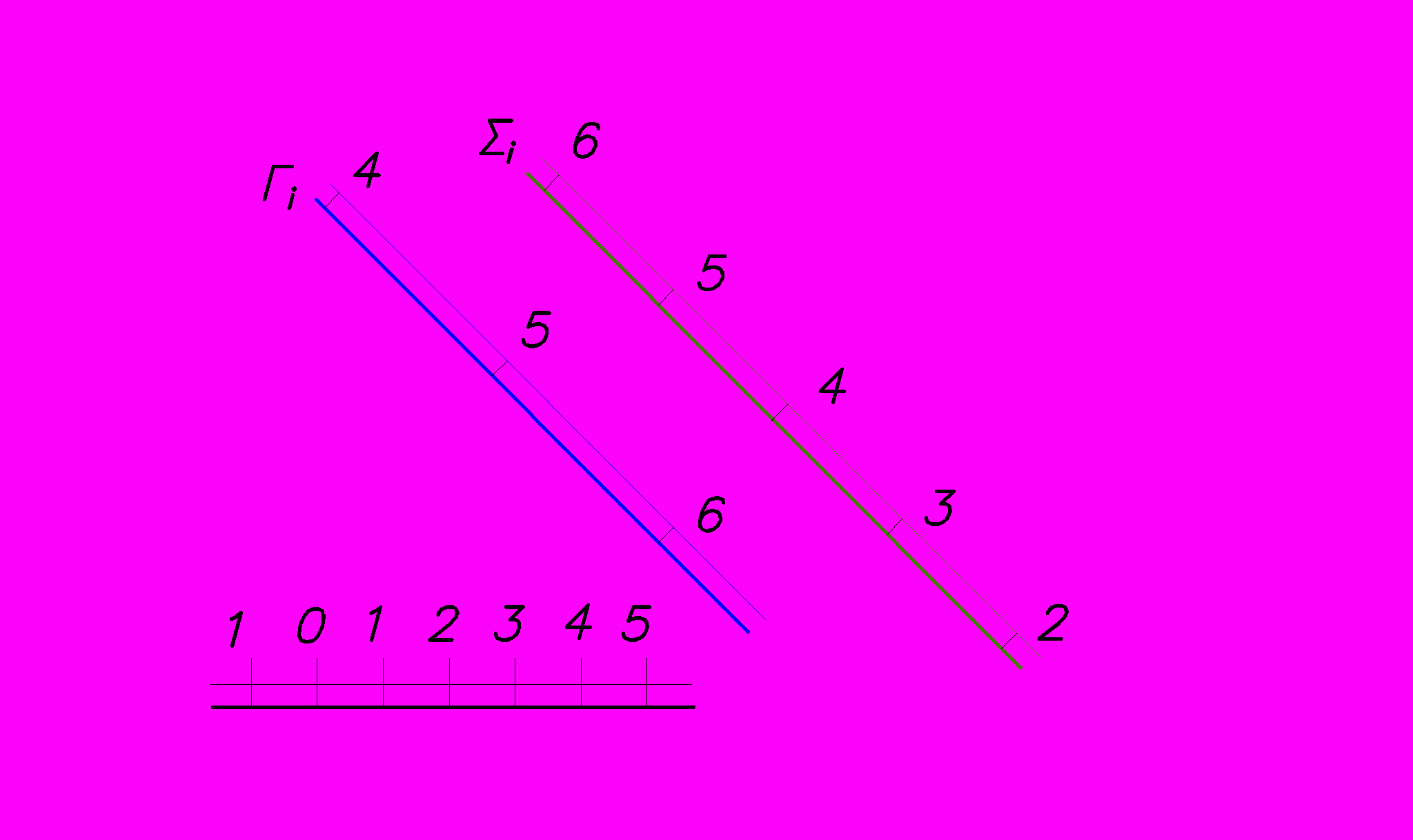
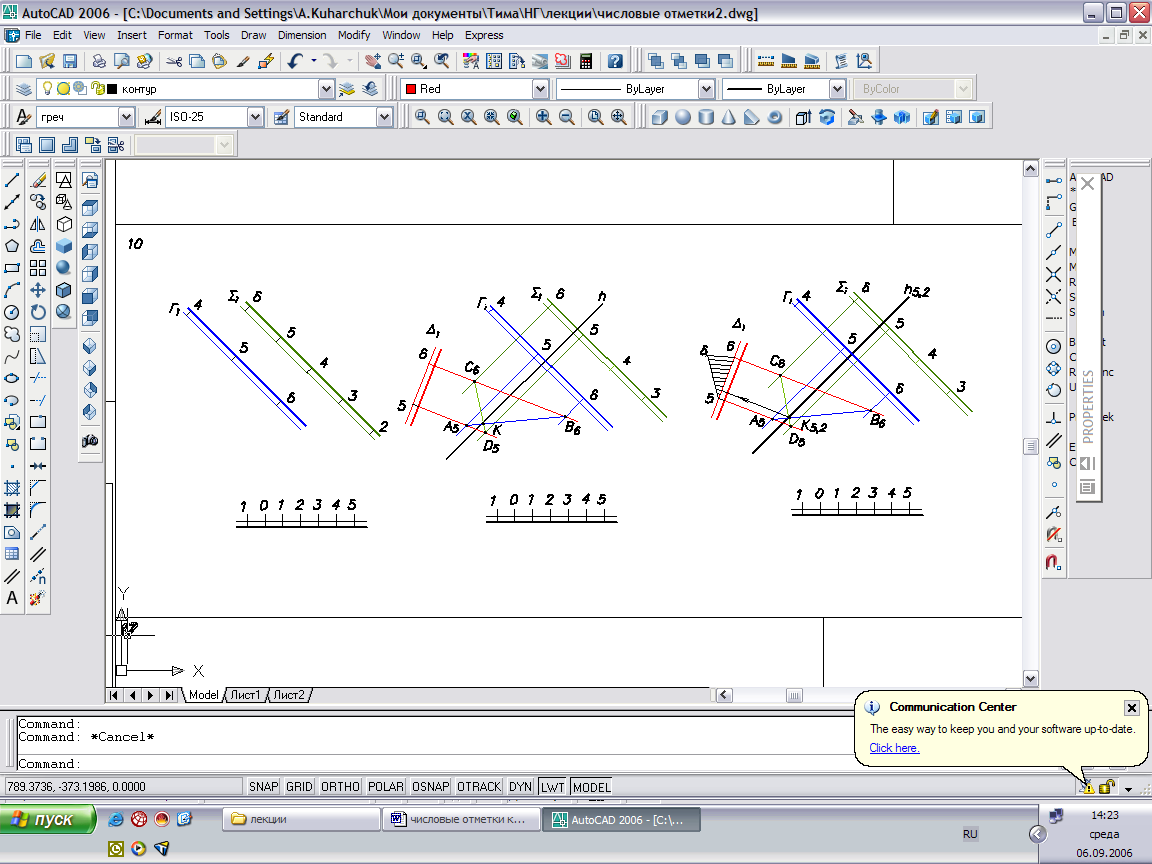
Рис. 48


Искомая прямая в данном случае будет общей горизонталью, проходящей через точку, общую для двух плоскостей.

Для решения используем вспомогательную плоскость общего положения D, которая пересекается с каждой из плоскосте по вспомогательным линиям АВ и СD:

D x Г = АВ, D x S = CD.

В свою очередь эти линии пересекаются в точке К, через которую проходит искомая горизонталь:

АВ x CD = К, К=h.

Для определения отметки горизонтали интервал вспомогательной плоскости D разбиваем на 10 отрезков, т.к. точка К находится также и на горизонтали этой плоскости.


Пример: Построить линию пересечения наклонного конуса, заданного вершиной S₇ и основанием (окружность–горизонталь h₂) c плоскостью, заданной масштабом падения.

Построим горизонтали конуса – окружности на оси конуса с центрами в точках градуирования оси и радиусом, определяемым точками касания к образующей.

Искомая линия пересечения – геометрическое место точек, общих горизонталям конуса и плоскости – соединяет точки пересечения горизонталей с одинаковыми отметками.



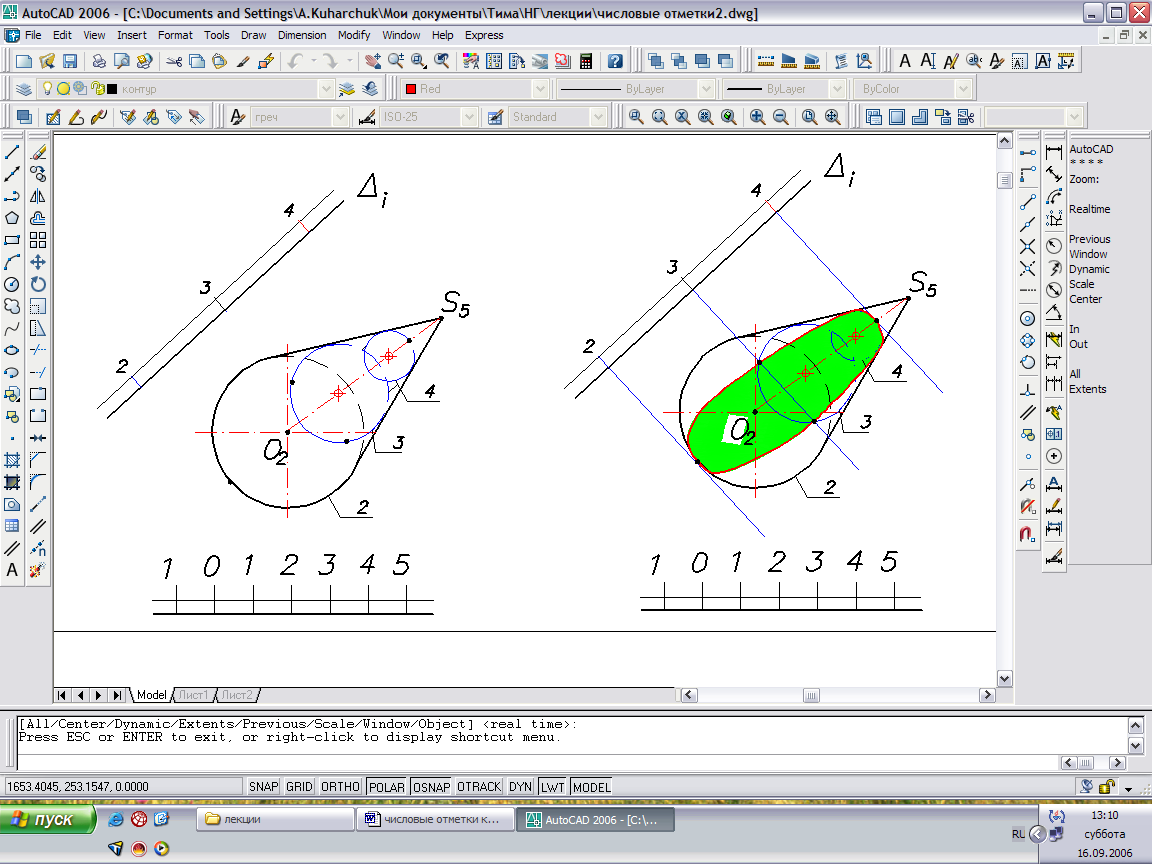
Рис. 49


Пример: Построить линию пересечения плоскостей откосов насыпи и выемки с топографической поверхностью при возведении площадки или дороги.

Случай 1: Площадка прямолинейная и горизонтальная. Уклон плоскости откосов насыпи i_Н=1:1. Уклон плоскости откосов выемки i_В=1:1,5.



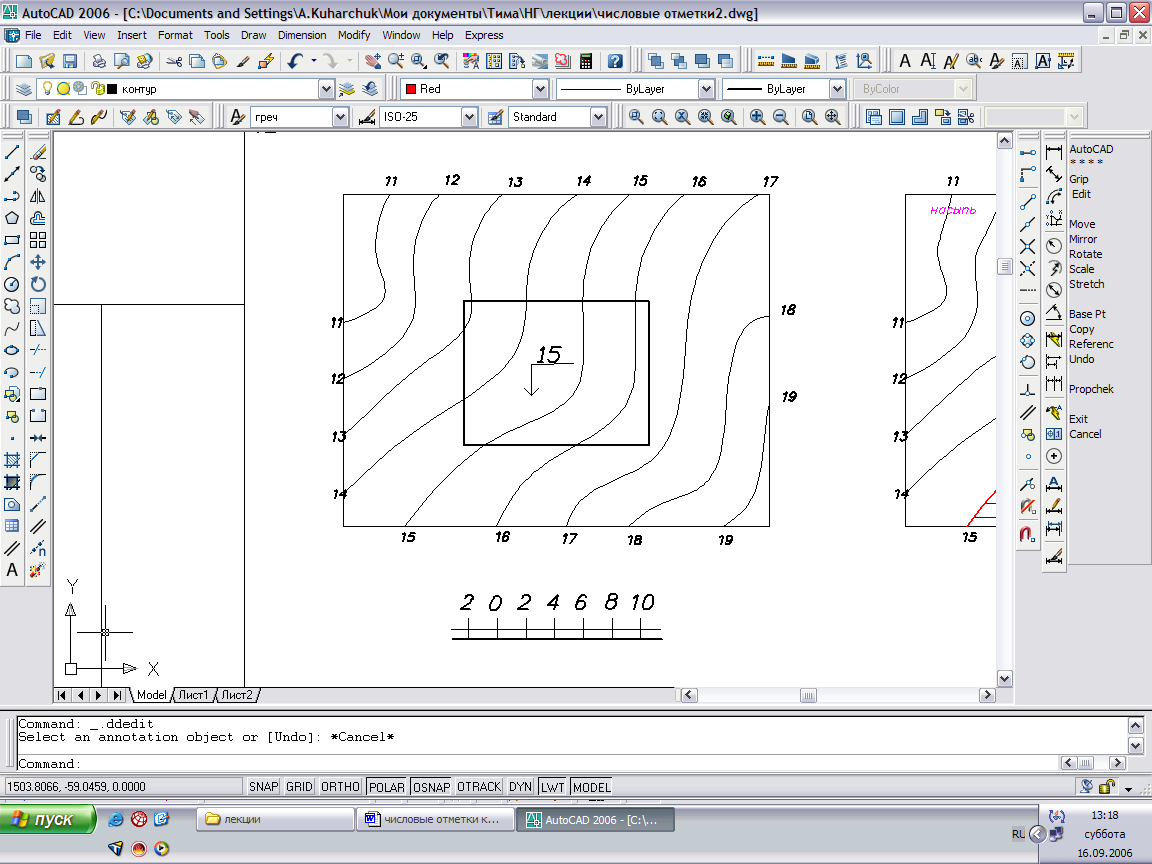
Рис.50


Порядок решения:

1. Находим границу нулевых работ, отделяющая насыпную часть площадки от той, что расположена в выемке – горизонталь, равная отметке площадки. Определяем зону выемки и насыпи. В зоне выемки предусматриваем кювет шириной 1 м для отвода ливневых вод.
   
2. Числовой масштаб переводим в линейный – находим длину отрезка, соответствующего 1м на местности.
   
3. Определяем интервал выемки и насыпи: L_В=1м, L_Н=1,5 м.
   
4. Строим каркас горизонталей насыпных откосов, эти горизонтали будут прямыми, параллельные соответствующим сторонам площадки, находящимися на расстоянии L_Н. Находим пересечение плоскостей откосов на пересечениях горизонталей с одинаковыми отметками. Плоскости одинакового уклона пересекаются по прямой, проекция которой является биссектрисой угла, образованного горизонталями этих плоскостей.
   

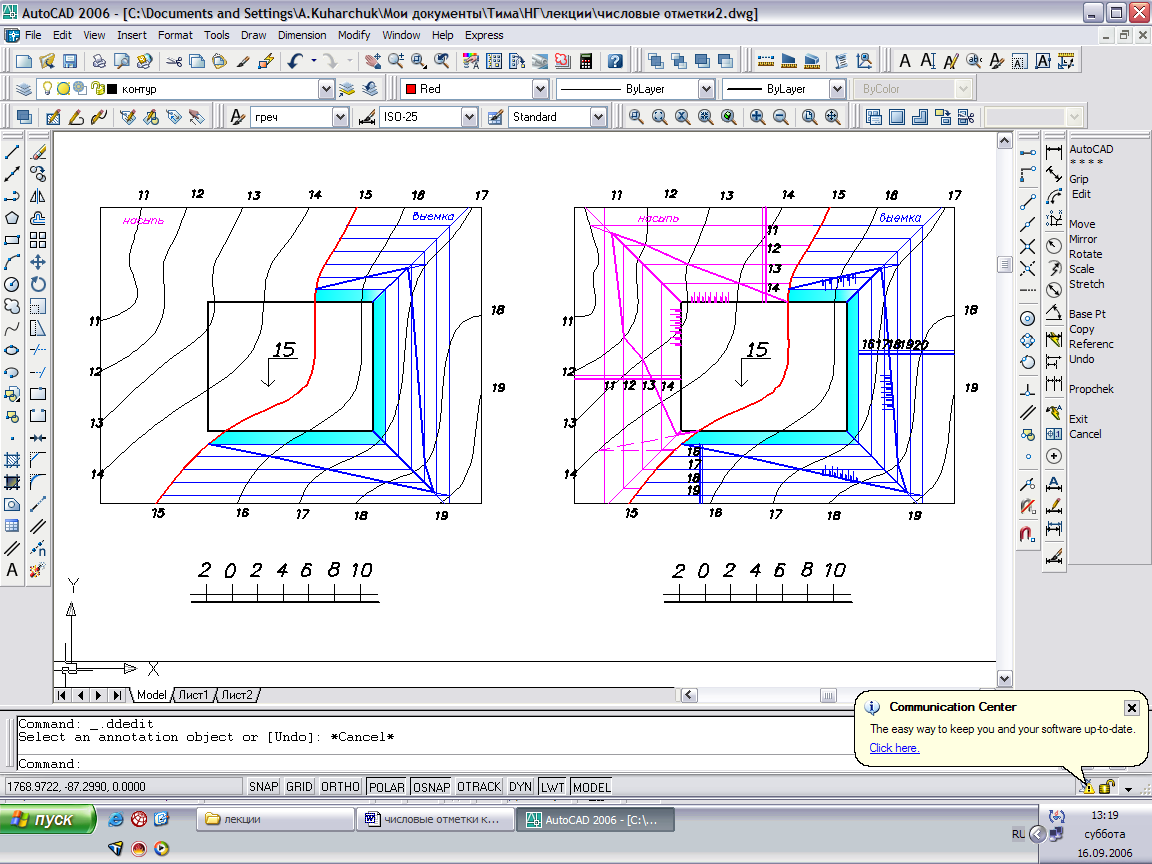
Рис.51

5. Находим точки пересечения горизонталей откосов и горизонталей топографической поверхности с одинаковыми отметками. Точки пересечения однозначных горизонталей соединяются между собой отрезками прямых. Линии пересечения плоскостей смежных откосов с рельефом должны сходиться в ону точку В на общем ребре АВ.
   
6. Для наглядности изображения откосы выделяют бергштрихами – чередующимися длинными и короткими штрихами у верхней кромки откоса. Направление бергштрихов указывают направление уклона.
   
7. Строим каркас горизонталей откосов выемки, находящиеся на расстоянии L_В, затем повторяем все действия начиная с п.4 для откосов выемки.
   

Случай 2: Полотно дороги прямолинейное, но не горизонтальное. Уклон плоскости дороги i_Д=1:5. Уклон плоскости откосов i_ОТК=1:1,5.



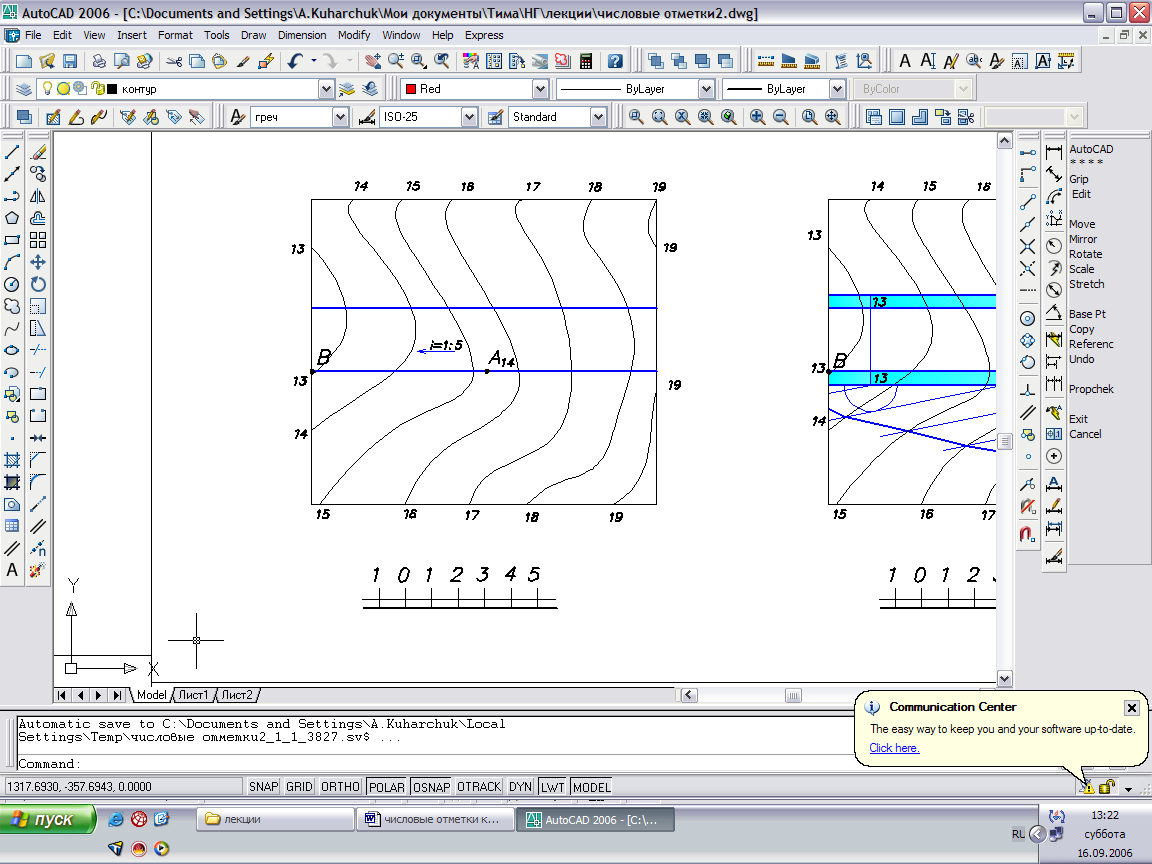
Рис.52


Решение задачи сводится к построению плоскости с уклоном i=1:1,5 прямую АВ – бровку дороги, имеющую уклон i=1:5. Искомая плоскость – касательная к конусу, вершина которого находится на одной из точек прямой АВ, образующая конуса имеет уклон i=1:1,5. Горизонталь плоскости – линия, проходящая через точку на прямой АВ и касательная к горизонтали конуса с той же отметкой.

Последовательность решения:

1. Проградуируем прямую АВ, L_AB = 5м.
   
2. В одной из точек на прямой, например с отметкой 15, располагаем вершину вспомогательного конуса с уклоном i=1:1,5. Интервал образующей конуса L=1,5м. Горизонталь конуса – окружность радиусом 1,5м имеет отметку h₁₆.
   

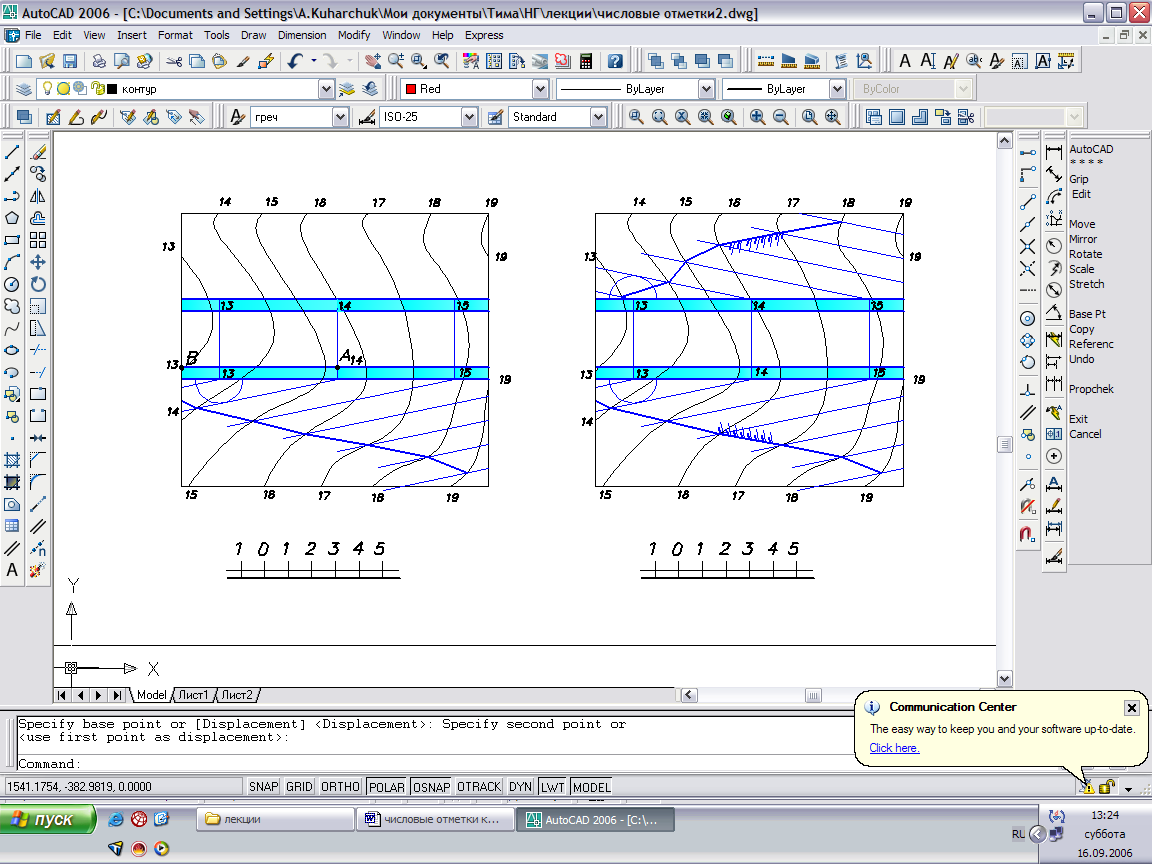
Рис.53

3. Проводим линию, касательную к горизонтали конуса h₁₆, проходящую через точку на прямой АВ с такой же отметкой – 16. Получили горизонталь плоскости откосов h₁₆, перпендикулярно которой на свободном месте чертежа строим масштаб падения и откладываем интервал заданной плоскости. Горизонтали этой плоскости параллельны и проходят через точки с теми же отметками на бровке дороги.
   
4. Находим линию пересечения плоскости откосов с топографической поверхностью и наносим бергштрихи, указывая направление уклона.
   

Случай 3: Полотно дороги непрямолинейное, и не горизонтальное. Уклон плоскости дороги i_Д=1:5. Уклон плоскости откосов i_ОТК=1:1,5.



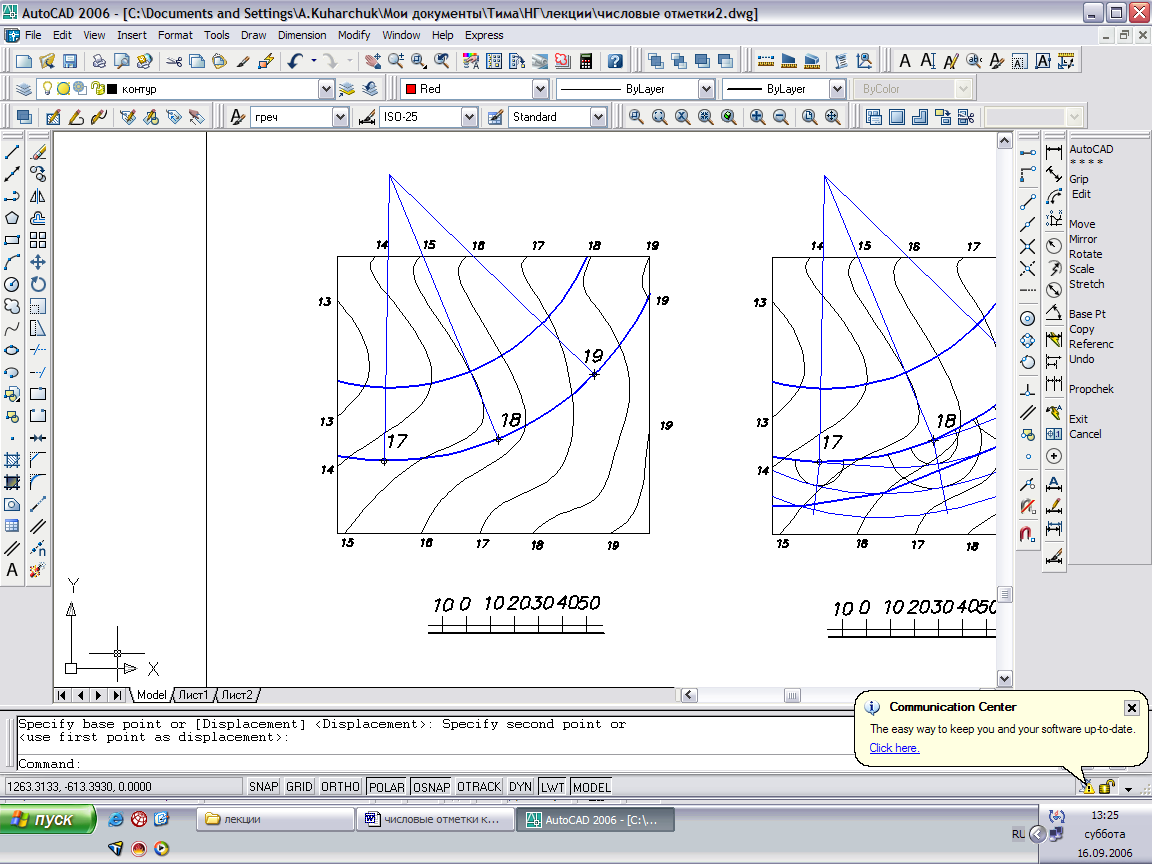
Рис.54

Решение задачи сводится к построению поверхности одинакового ската через кривую линию - бровку дороги, имеющую уклон i_Д=1:5, а следовательно интервал , L_AB = 5м. Поверхность одинакового ската имеет уклон i_ОТК=1:1,5, а следовательно интервал L_ОТК=1,5м.

Последовательность решения:

1. Проградуируем линию АВ, L_AB = 5м.
   
2. В одной из точек на линии, например с отметкой 15, располагаем вершину вспомогательного конуса с уклоном i=1:1,5. Интервал образующей конуса L=1,5м. Горизонталь конуса – окружность радиусом 1,5м имеет отметку h₁₆.
   
3. В точке с отметкой 14 на линии располагаем вершину еще одного такого же вспомогательного конуса. Горизонтали конуса – окружности радиусом 1,5м и отметкой h_15, радиусом 3м и отметкой h₁₆.
   
4. Для следующей точки с отметкой 13 проводим три окружности – горизонтали h_14, h_15, h_16. И так далее для всех остальных точек.
   

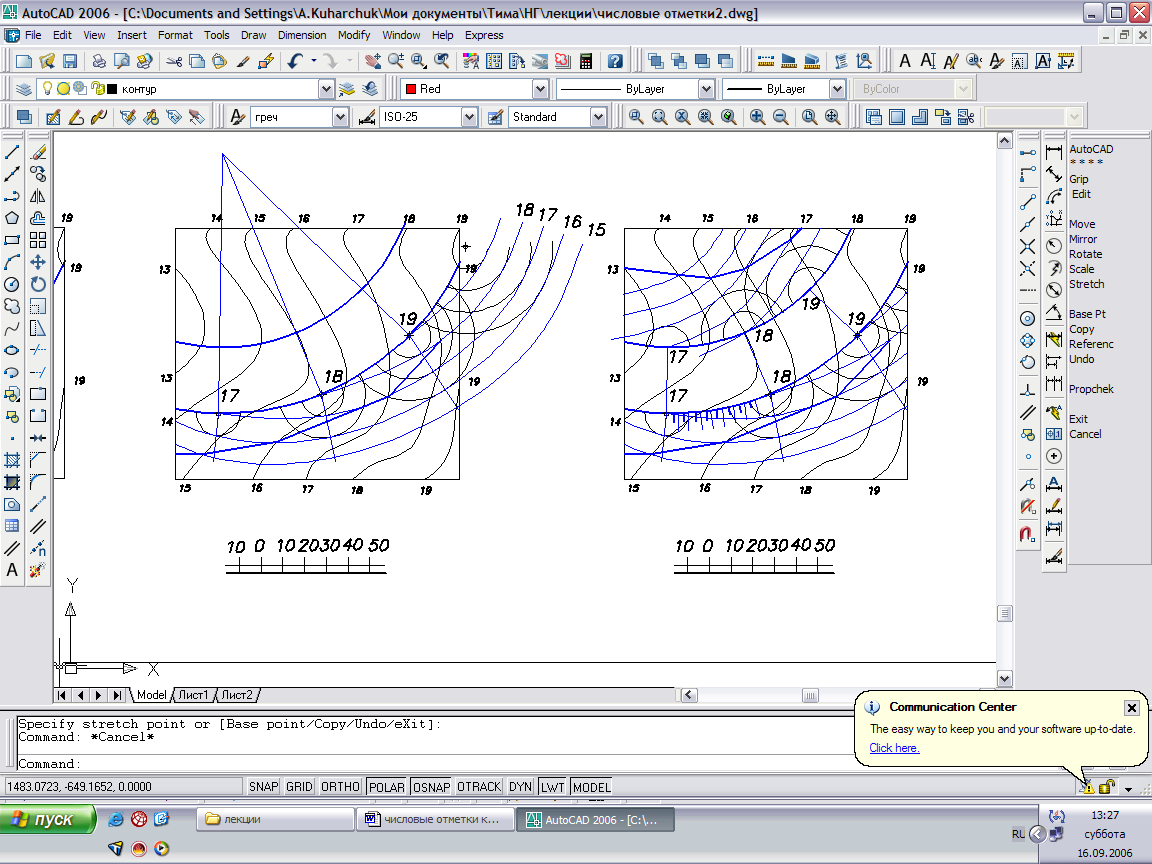
Рис.55

5. Проводим линию, касательную ко всем горизонталям конусов с отметкой h₁₆. Получили горизонталь поверхности откоса h₁₆ – поверхности одинакового ската. Следующая горизонталь h₁₅ – огибающая окружности с отметкой h_15, и т.д. Все горизонтали поверхности откоса эквидистантны и проходят через точки с теми же отметками на бровке дороги.
   
6. Находим линию пересечения поверхности откосов с топографической поверхностью и наносим бергштрихи, указывая направление уклона.
   

Решение 1 ГПЗ (пересечение линии и поверхности)


При нахождении точки М пересечения линии а и поверхности Σ используется метод заключения линии во вспомогательную плоскость-посредник Δ. В качестве такой плоскости-посредника используется проецирующая или произвольная плоскость. Для решения задачи в проекциях с числовыми отметками чаще всего удобно использовать произвольную плоскость-посредник. Плоскость-посредник Δ пересекается с исходной поверхностью Σ по линии b, которая определяется пересечением одноименных горизонталей. Пересечение линий а и b дает точку пересечения М = а х Σ.

Алгоритм решения:

1. Для решения задачи вводим вспомогательную плоскость-посредник общего положения Г, проходящую через заданную прямую а.
   
2. Находим линию пересечения плоскости-посредника с исходной плоскостью: Г x Σ = b.
   

3. Точка пересечения линий а и b– и есть точка пересечения линии и поверхности: b x а = М => а x Σ = М.




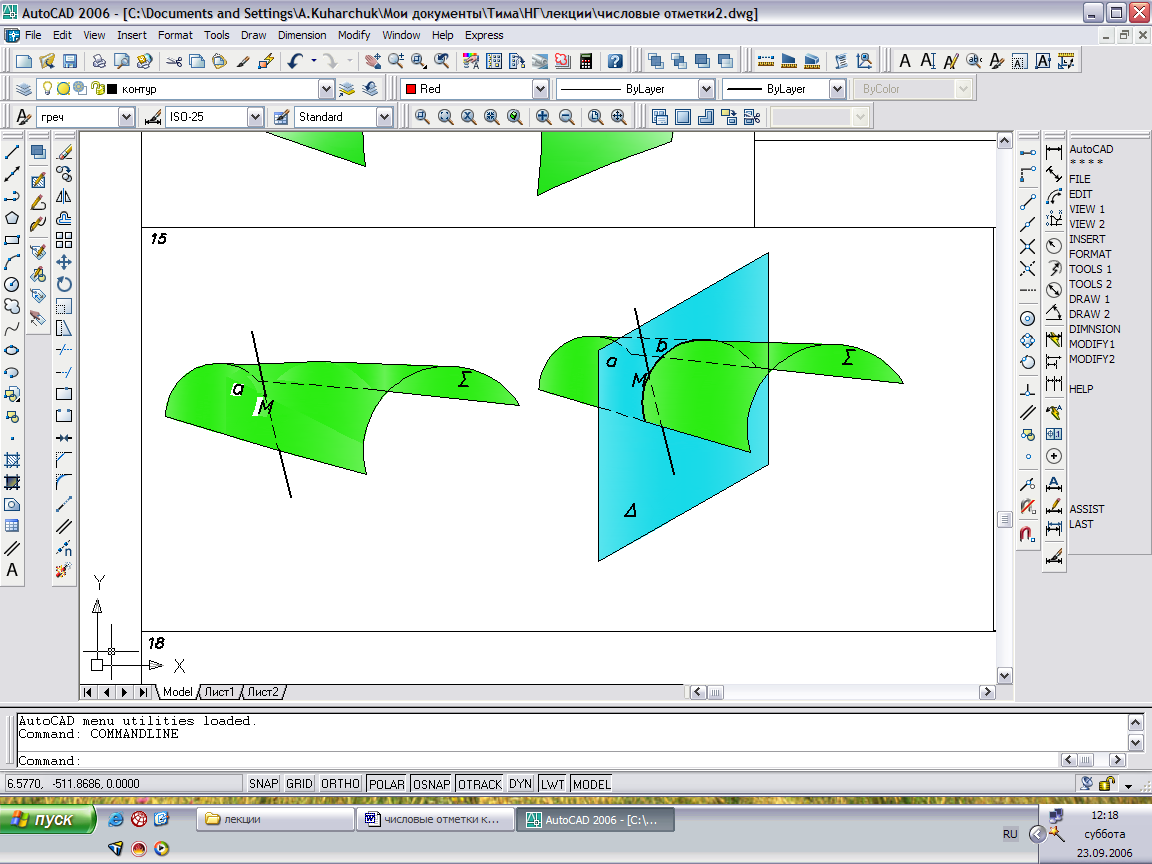
Рис. 56


Пример: Определить точку пересечения К линии АВ и плоскости Σ.



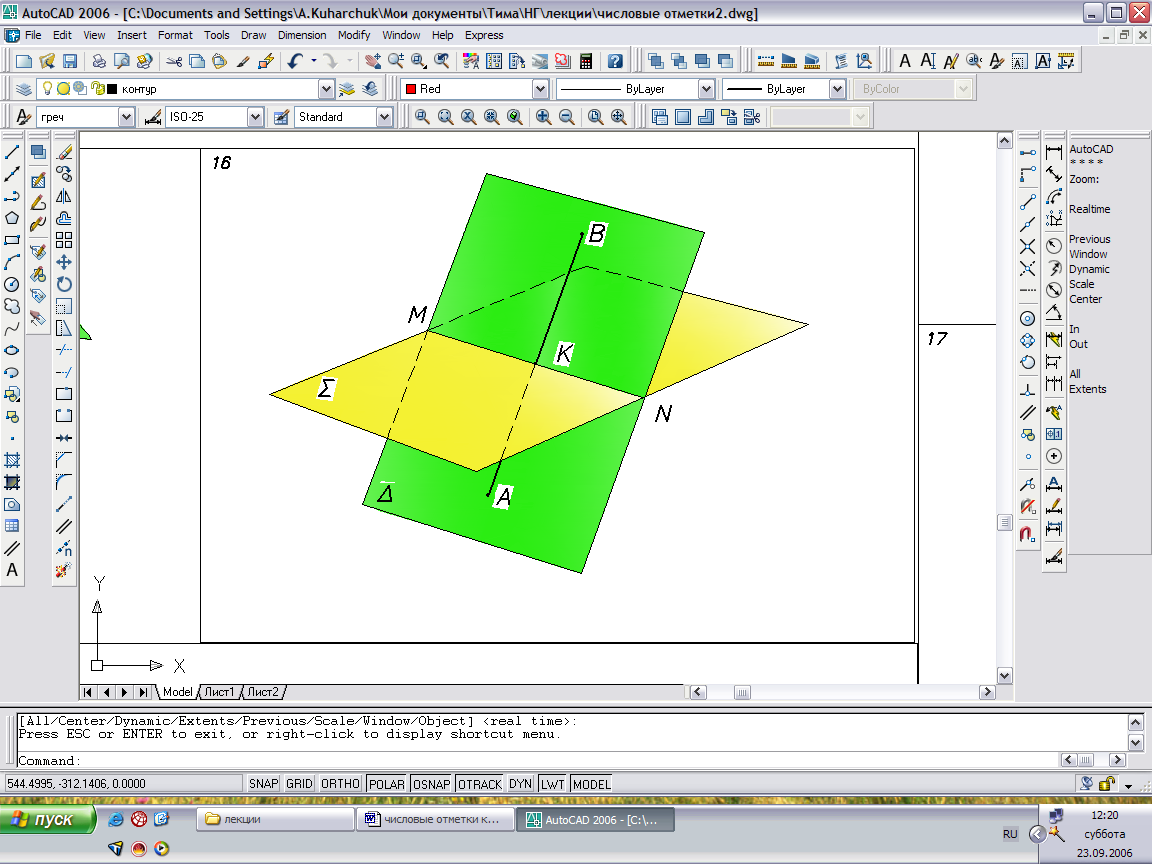
Рис. 57

Порядок решения:

1. Через прямую А₅В₇ проводим плоскость-посредник Δ общего положения. Для этого сначала проградуируем прямую. Направление горизонталей плоскости нужно выбрать так, чтобы в пределах чертежа получить нужные для дальнейших построений точки N_5, M_8.

2. Плоскость-посредник Δ пересекает исходную плоскость по линии N₅M₈, где точки N_, и M - точки пересечения одноименных горизонталей плоскостей Δ и Σ.

3. Точка пересечения линий МN и АВ – искомая точка K пересечения прямой и плоскости.

5. Видимость прямой определяется по методу конкурирующих точек: в месте пересечения прямой и горизонтали плоскости Σ видим ту точку, у которой отметка выше.
   

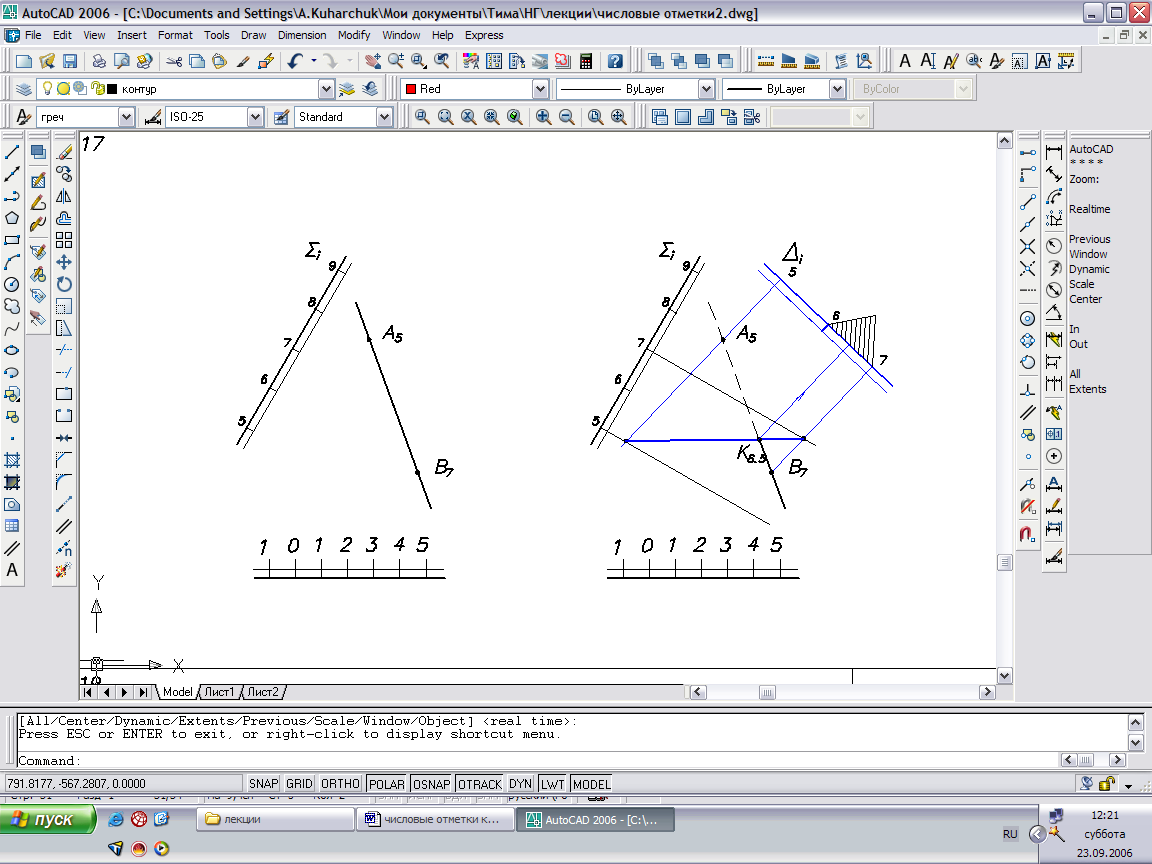
Рис. 58

Пример: Определить точку пересечения линии общего положения МN и поверхности многогранника Σ.



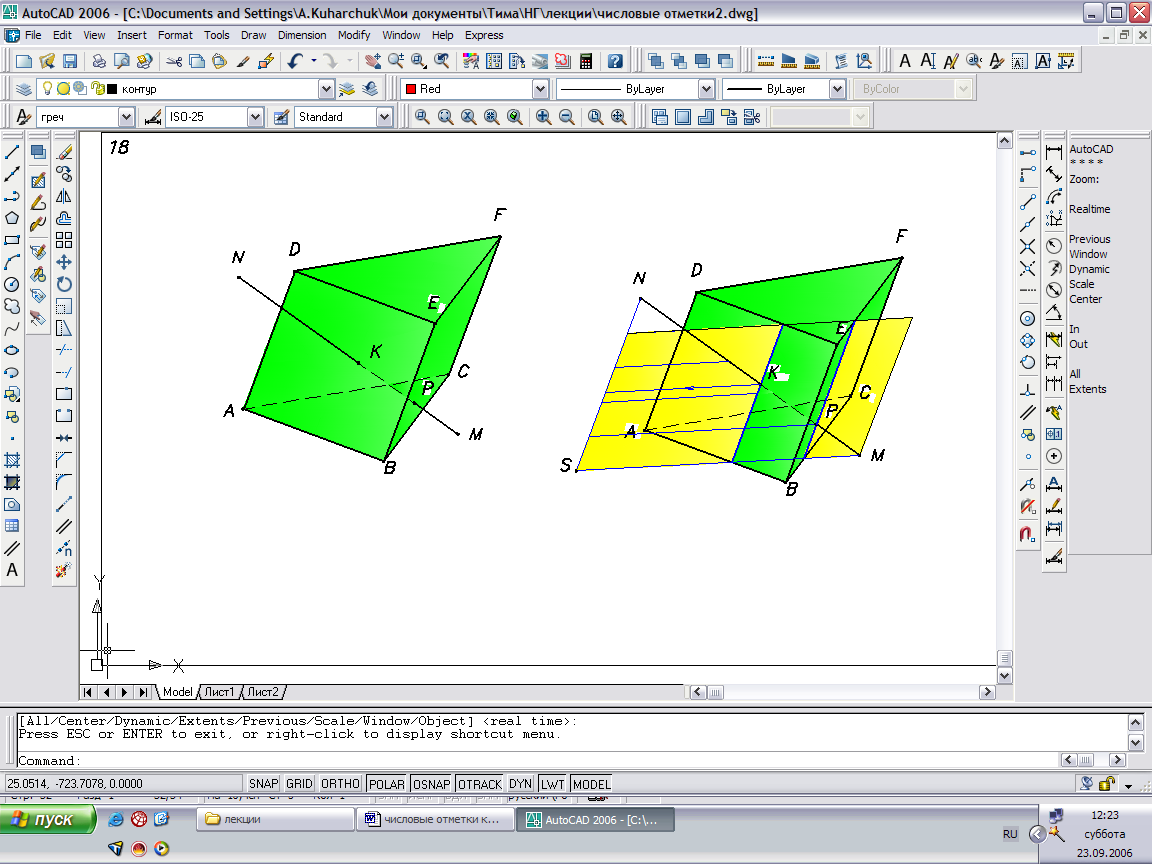
Рис. 59



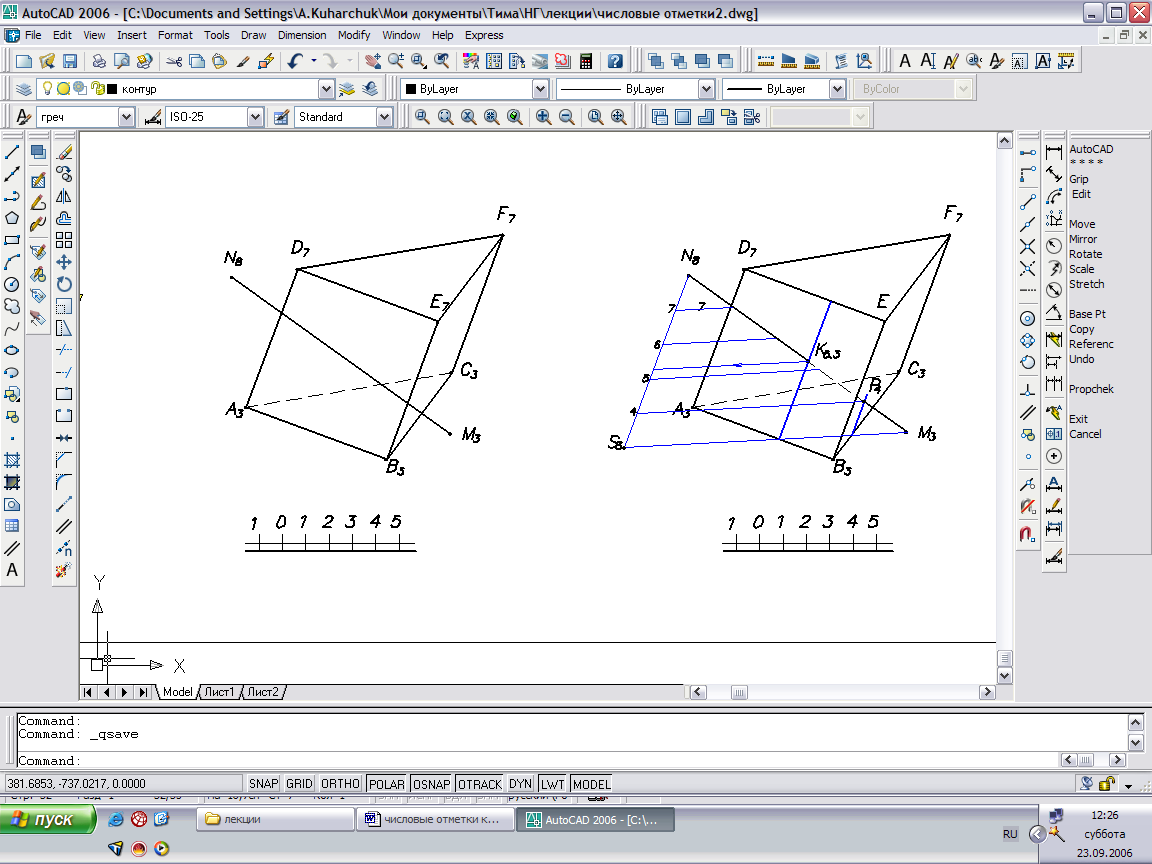
Рис. 60

Порядок решения:

1. Через прямую М₃N₈ проводим плоскость-посредник Δ, параллельную ребрам призмы. Для этого через точку N₈ проведем линию N₈S₃, параллельную ребрам AD, BE, CF (по трем условиям параллельности прямых).
   
2. Линия M₃S₃ - линия пересечения вспомогательной плоскости Δ с основанием А₃B₃C_3.
   
3. Плоскость-посредник Δ пересекает боковые грани призмы по линиям p,q, проходящим через точки P,Q, параллельным ребрам призмы.
   
4. Точки пересечения линий p,q с прямой МN – искомые точки K,L пересечения прямой и поверхности.
   
5. Видимость прямой определяется по методу конкурирующих точек: в месте пересечения прямых видим те точки, у которых отметка выше.
   

Частный случай: Определить точку пересечения горизонтали МN и плоскости Σ.



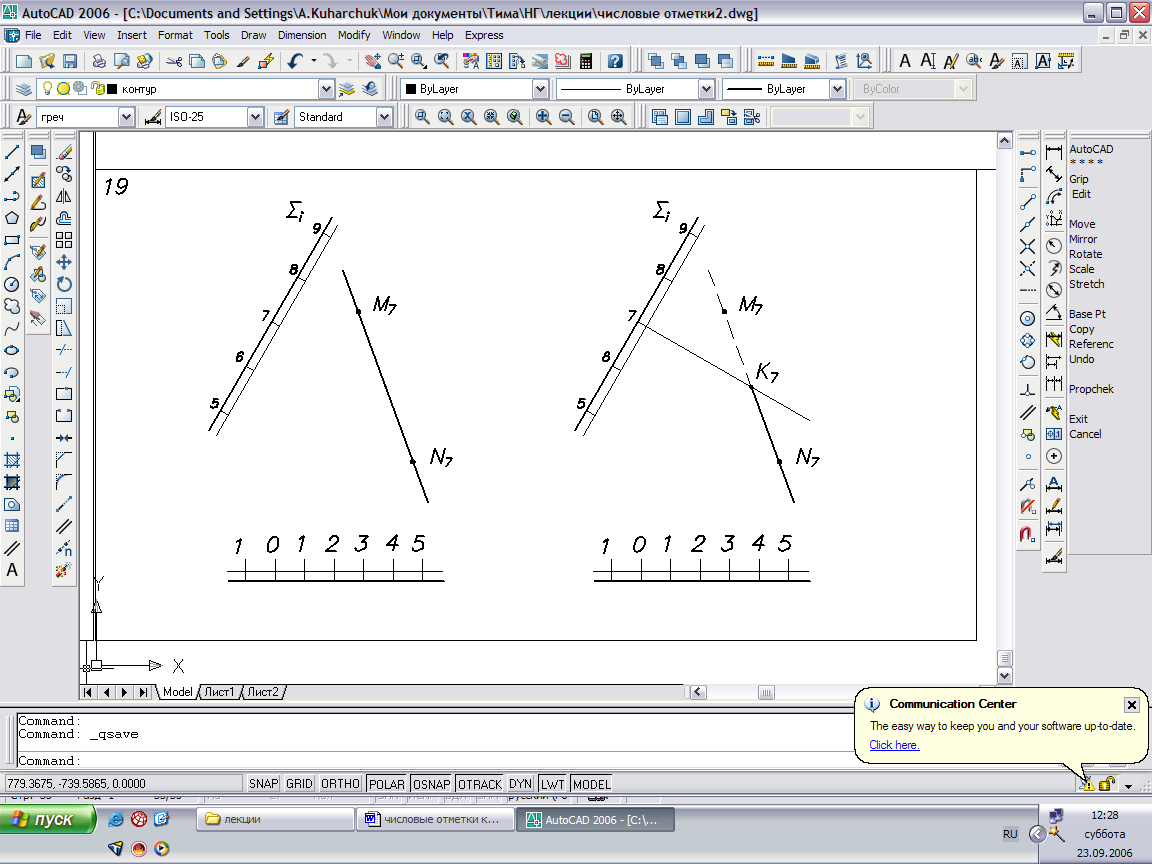
Рис. 61


Метрические задачи.


Метрическими принято называть задачи, включающие в себя определение натуральных величин длин, углов, площадей, объемов и т.д., т.к. при проецировании натуральные величины искажаются. Среди метрических задач выделяют две основные:

1 ОМЗ (1 основная метрическая задача) – определение натуральной величины отрезка;

2 ОМЗ (2 основная метрическая задача) – построение перпендикуляра к плоскости.


Решение 1 ОМЗ (определение натуральной величины отрезка)


Отрезки горизонталей проецируются в натуральную величину соответственно на горизонтальную плоскость проекции.  Во всех остальных случаях отрезки прямых проецируются с искажением.

Расстояние между двумя точками А и В равно боковой стороне АВ трапеции АВВ₅А₂ Обычно для определения натуральной величины отрезка используют не трапецию, а прямоугольный треугольник, образованный двумя катетами: первый катет – проекция отрезка, второй катет - превышение Δh в масштабе чертежа; гипотенуза этого треугольника определяет натуральную величину отрезка. Плоскость, в которой лежит этот треугольник вращается до совмещения с плоскостью проекций. Способ определения натуральной величины отрезка называется способом прямоугольного треугольника.



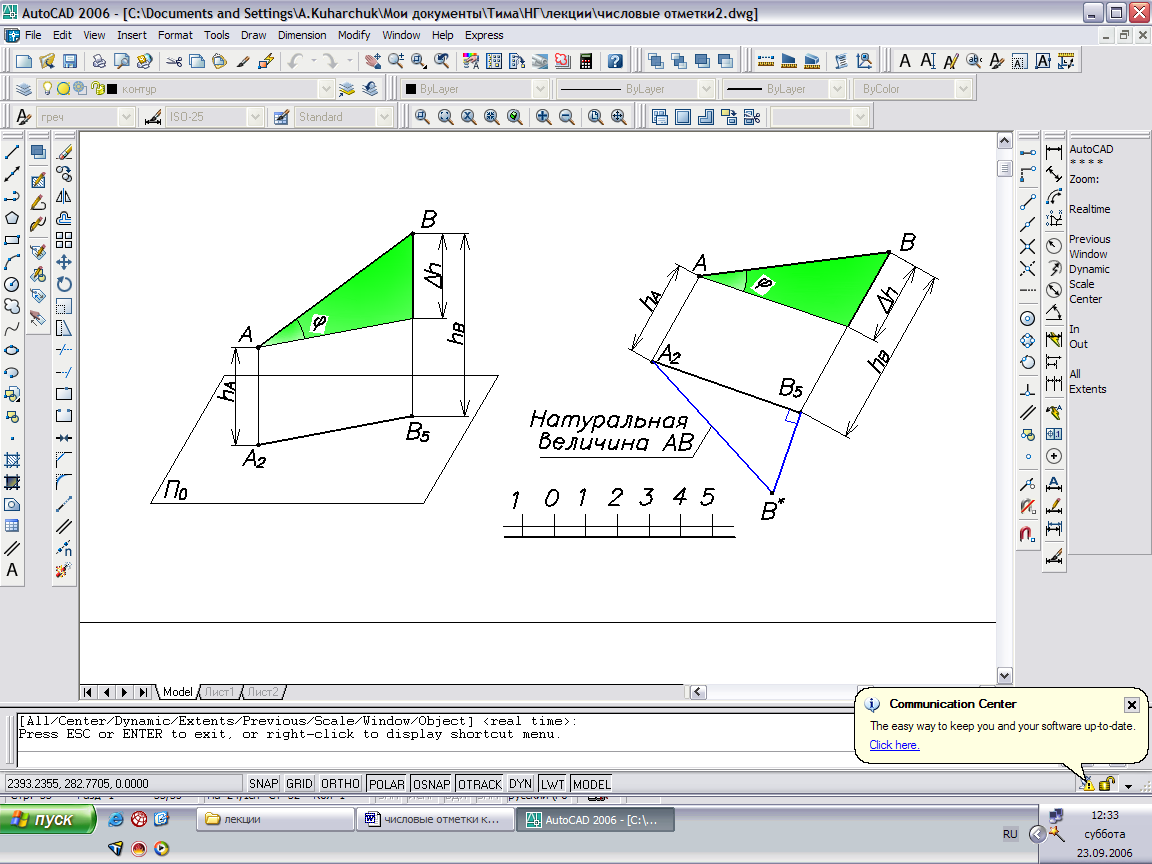
Рис. 62


Решение 2 ОМЗ (построение перпендикуляра к плоскости)


Чтобы восстановить из заданной точки перпендикуляр к плоскости, по теореме о перпендикулярности прямой и плоскости, необходимо

1. через точку провести проекцию прямой параллельно масштабу падения плоскости;
   
2. определить интервал прямой с помощью прямоугольного треугольника,
   
3. проградуировать прямую так, чтобы числовые отметки прямой и плоскости возрастали в противоположных направлениях.
   

Комплексные задачи


Комплексные задачи – задачи, требующие применения правил решения позиционных и метрических задач.

Пример: Определить расстояние от точки А до плоскости Σ.



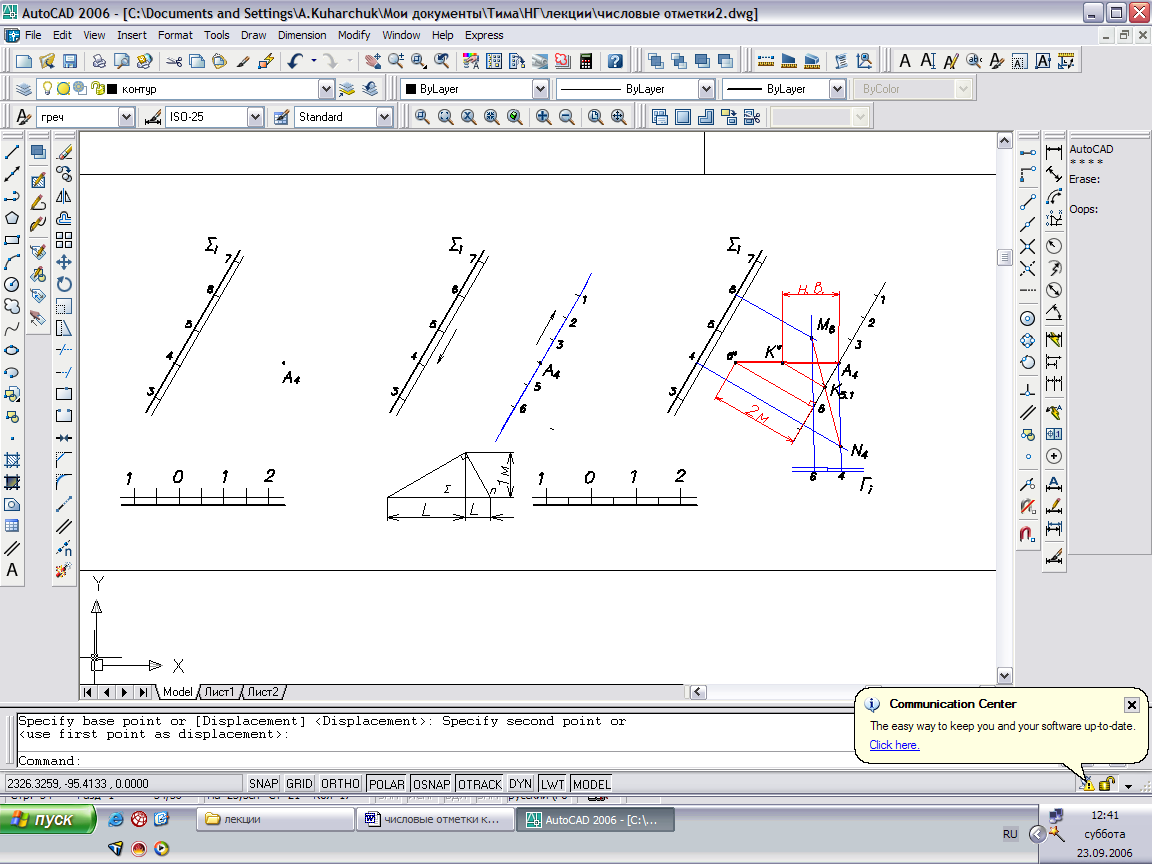
Рис. 63

Порядок решения:

1. проводим проекцию перпендикуляра к плоскости Σ параллельно масштабу падения Σ_i ;
   
2. с помощью прямоугольного треугольника определяем интервал L_n перпендикуляра. Треугольник построен по отрезку L_Σ гипотенузы и высоте h, равной 1 м в масштабе чертежа. Второй отрезок АD гипотенузы будет равен интервалу перпендикуляра L_n;
   
3. градуируем проекцию перпендикуляра: получаем точки с отметками 3,2,1;
   
4. через перпендикуляр к плоскости Σ проводим вспомогательную плоскость Г горизонталями с отметками 6 и 4 (h₆h₄);
   
5. строим прямую М₆ N₄ пересечения плоскостей Σ и Г;
   
6. отмечаем точку К_h , в которой проекция перпендикуляра пересекает прямую М₆ N₄, точка К является основанием перпендикуляра, опущенного из точки А на плоскость Σ;
   
7. определяем натуральную величину отрезка КА – перпендикуляра к плоскости. Так как отметка точки ^ К неизвестна, то сначала находим натуральную величину того отрезка перпендикуляра, отметки которого 6 и 4. Затем на гипотенузе находим точку K^*. Отрезок А^*К^* будет искомым расстоянием от т. А до плоскости Σ.
   

Способ вращения вокруг горизонтали


Способ вращения вокруг горизонтали применяется в основном для решения задачи преобразования плоскости общего положения в плоскость уровня. Суть способа заключается в том, что плоскость общего положения, поворачивается вокруг прямой уровня до состояния, параллельного горизонтальной плоскости проекций П₀. Рассмотрим поворот точки А вокруг горизонтали h до уровня горизонтали. Точка А движется по дуге окружности радиуса R с центром в точке O, принадлежащей горизонтали h. Радиус R является гипотенузой прямоугольного треугольника А₅А^*O₃, где один катет А₅О₃ - горизонтальная проекция радиуса вращения, другой - равен h - расстояние между точкой A и прямой h по вертикали. А' - новое положение точки А. Мы повернули плоскость, в которой вокруг прямой h до состояния, параллельного П₀, поэтому полученная проекция является проекцией в натуральную величину.



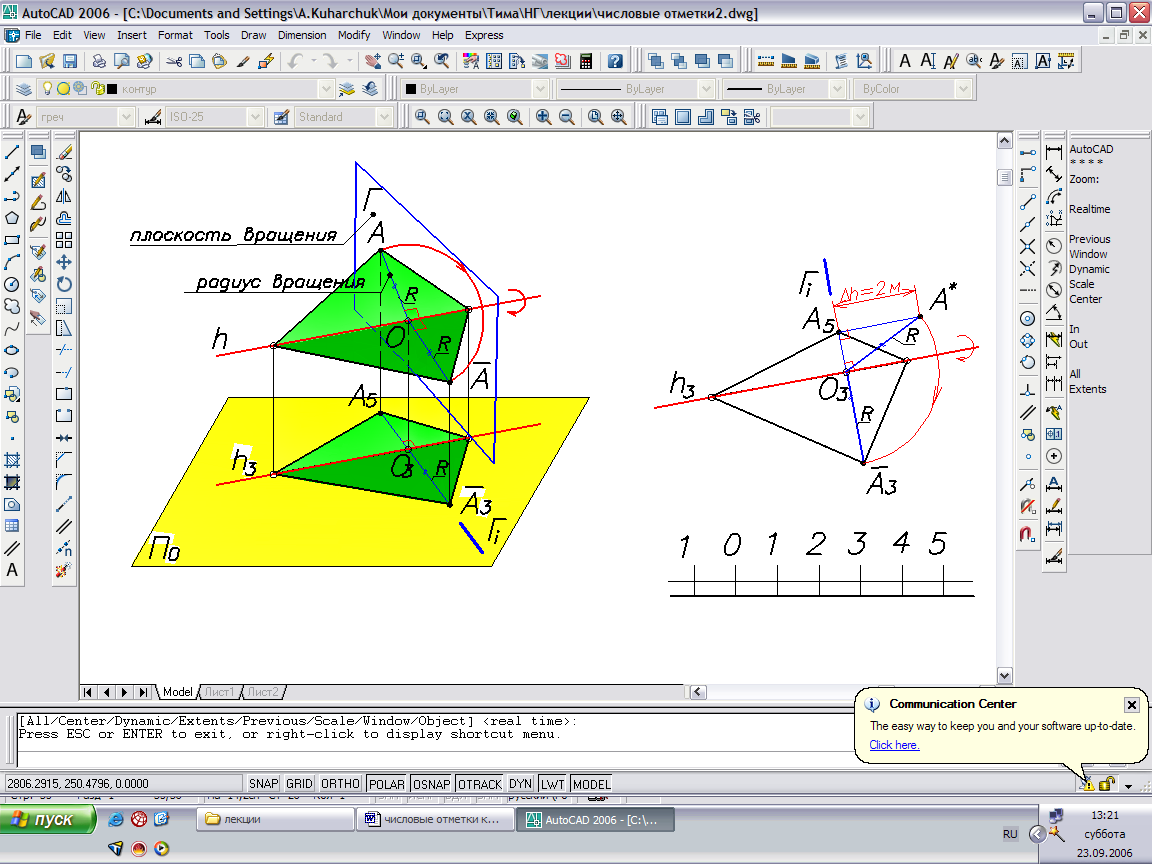
Рис. 64


Пример: Найти центр S описанной окружности треугольника АВС.

Плоскость треугольника АВС является плоскостью общего положения, которая проецируется на П₀ с искажением. Для определения натуральной величины треугольника повернем его вокруг горизонтали h₂ до совмещения с горизонтальным положением. Точка В вращается в плоскости Г, перпендикулярной горизонтали, по окружности радиуса ОВ c центром О₂ на горизонтали. Точка С₂ лежит на горизонтали (оси вращения) и, следовательно остается неподвижной также как и точка 2 (точка пересечения АВ с горизонталью). После определения натуральной величины треугольника находим центр описанной вокруг него окружности на пересечении срединных перпендикуляров к двум любым сторонам. Чтобы определить положение центра в исходной плоскости, привязываем т. S к линии на плоскости и вращаем в обратном направлении. Точка имеет ту же отметку, что и горизонталь.

Порядок решения:



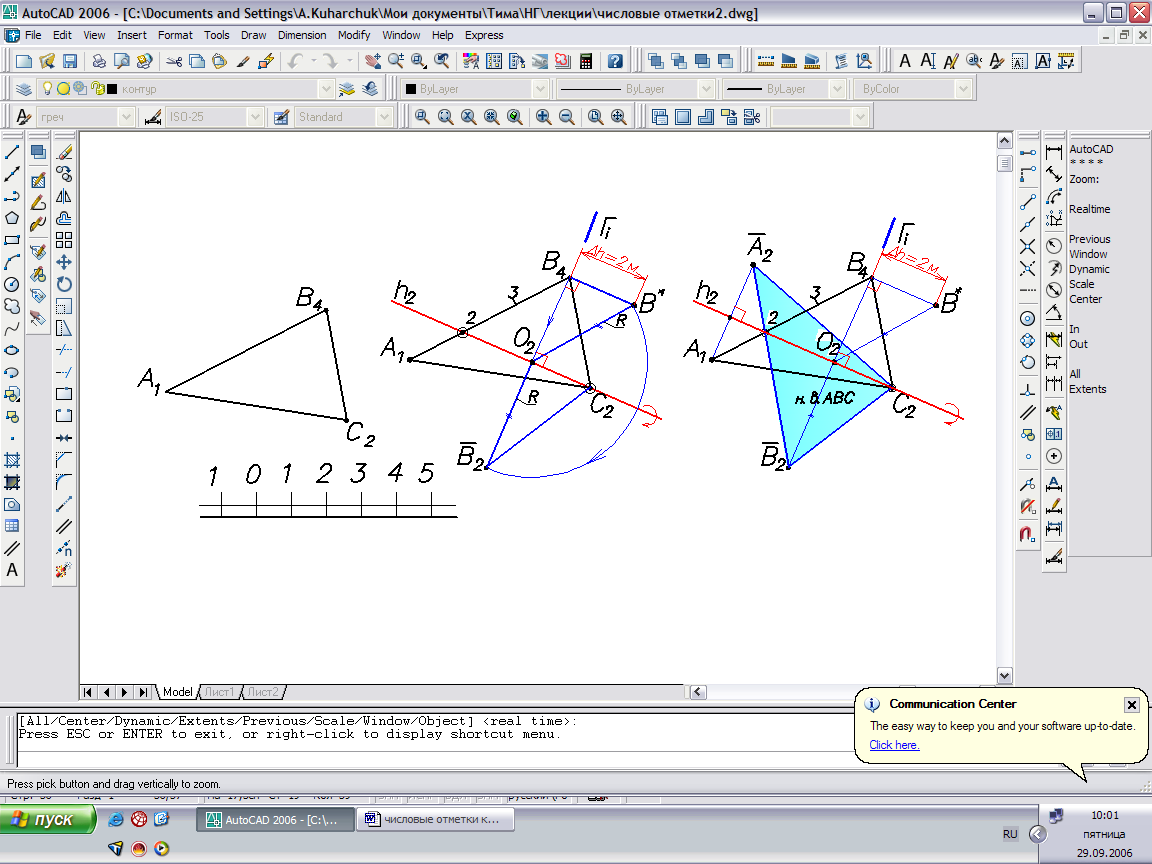
Рис. 65

1. Проводим горизонталь плоскости ^ АВС. Для этого проградуируем отрезок АВ и соединим точку 2 с точкой С.
   
2. Определим плоскость вращения точки В, центр и радиус ее вращения. Точка В вращается в плоскости Г проецирующей к П₀, перпендикулярной горизонтали. Проводим перпендикуляр из точки В₄ к h₂. Точка О₂ – центр вращения. О₂В₄ – радиус вращения. Находим натуральную величину радиуса вращения методом прямоугольного треугольника.
   
3. Находим натуральную величину треугольника ^ АВС, повернутого в плоскости П₂. Точка В перемещается вдоль линии В₂О₄ на величину, равную натуральной величине ОВ. Точка А₁ вращается в плоскости, параллельной Г и после поворота находится на продолжении линии В₂2. Точка С₂ лежит на горизонтали и остается на месте. Соединив А₂В₂С₂ получим натуральную величину треугольника.
   
4. Находим центр S₂ описанной окружности на пересечении срединных перпендикуляров к сторонам А₂С₂ и В₂С₂.
   

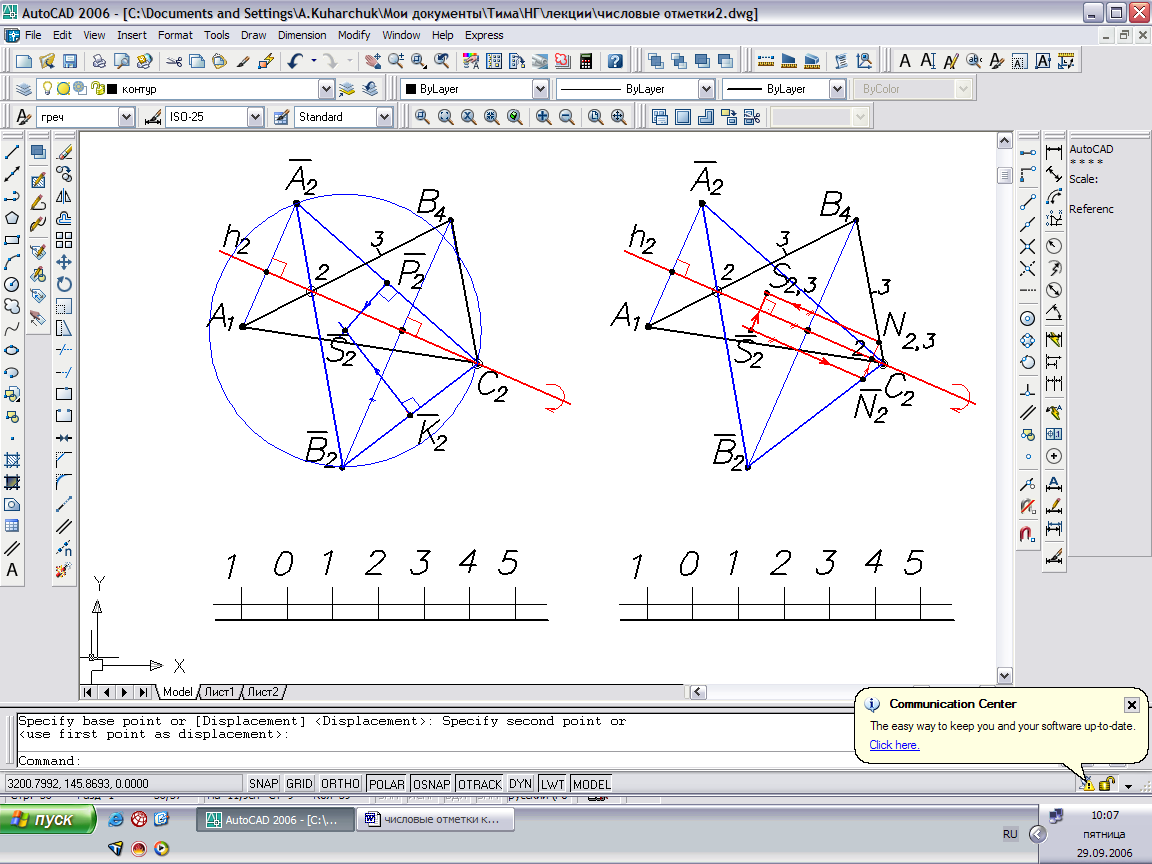
Рис. 66

5. Находим положение точки ^ S в исходной проекции плоскости. Проводим через S₂ линию, параллельную горизонтали до пересечения с В₂С₂, затем вращаем полученную точку N₂ перпендикулярно горизонтали до пересечения с В₄С₂, получаем точку N_2,3, на которой и будет находиться искомая точка S – центр окружности, описанной около треугольника.
   

Пример: Определить расстояние от точки С до линии АВ.


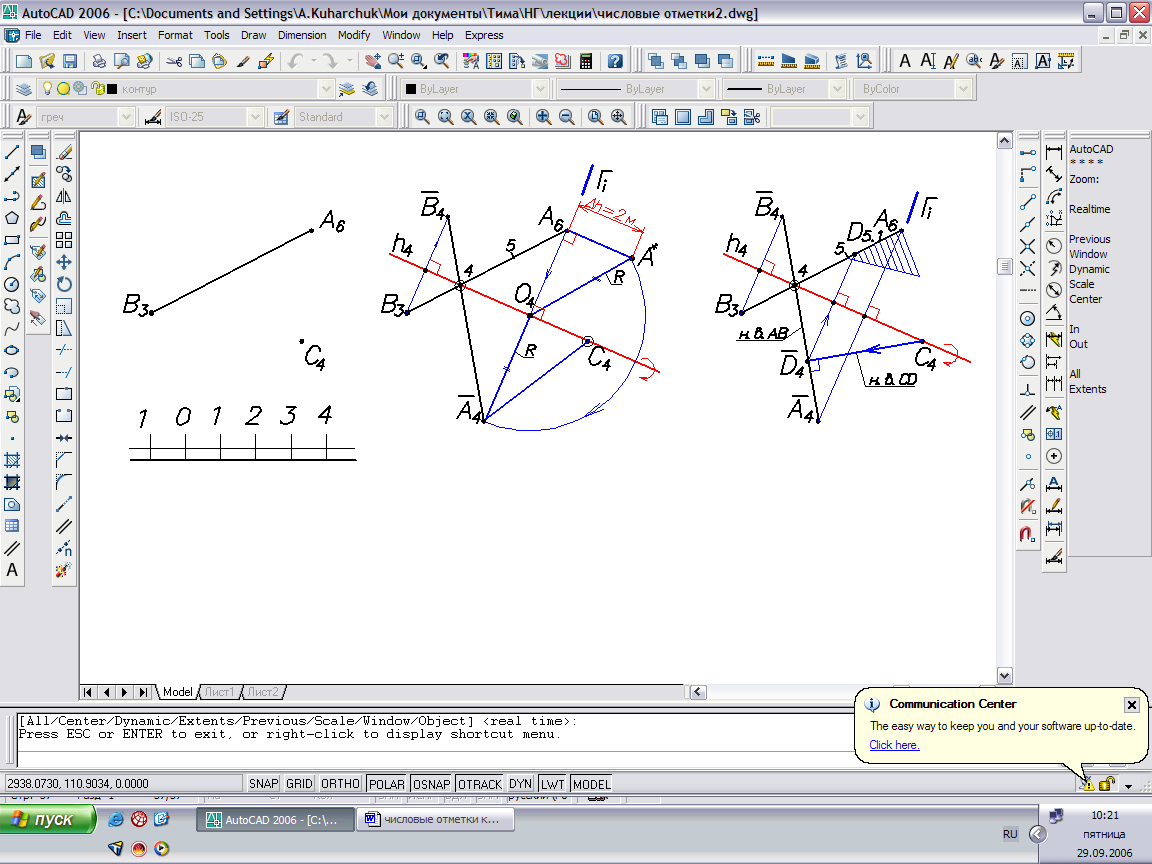
Рис. 67


Точка С и линия АВ образуют плоскость общего положения АВС. Для решения задачи находим натуральную величину треугольника АВС вращением вокруг горизонтали h₄ и восстанавливаем перпендикуляр из точки С₄ к повернутой линии А₄В₄. Отрезок D₄С₄ – натуральная величина расстояния от точки С до линии АВ. Чтобы найти точку D на исходной проекции АВ, вращаем эту точку в обратном направлении вокруг горизонтали h₄. Отметку точки D определяем по вспомогательной прямой, разбитой на 10 единиц.


Вопросы к экзаменационным билетам

1. Метод проецирования. Виды проецирования. Свойства ортогонального проецирования (позиционные свойства, метрические свойства).
   
2. Обратимость чертежа. Образование комплексного чертежа. Проекции с числовыми отметками. Масштаб числовой и линейный.
   
3. Задание линий общего положения. Заложение, превышение, уклон, интервал прямой. Градуирование прямой. Определение натуральной величины. Линии частного и общего положения. Взаимное расположение прямых.
   
4. Задание плоскости. Главные линии плоскости. Масштаб падения плоскости. Интервал плоскости. Направление простирания и угол простирания плоскости. Свойства принадлежности точки и линии плоскости. Построение плоскости с заданным уклоном через аданную прямую.
   
5. Взаимное асположение двух плоскостей. Взаимное расположение прямой и плоскости. Теорема о перпендикулярности прямой и плоскости.
   
6. Задание поверхностей. Определитель и закон образования поверхности. Линейчатые поверхности. Топографические поверхности. Поверхности одинакового ската.
   
7. Позиционные задачи. Виды позиционных задач. Решение II ГПЗ. Пересечение плоскостей. Пересечение поверхностей. Построение откосов насыпи или выемки горизонтальной площадки и наклонной дороги.
   
8. Позиционные задачи. Виды позиционных задач. Решение I ГПЗ. Пересечение линии и поверхности.
   
9. Метрические задачи. 1-я основная метрическая задача.
   
10. Метрические задачи. 2-я основная метрическая задача.
    
11. Комплексные задачи.
    
12. Преобразование чертежа. Способ вращения вокруг горизонтали.