В. И. Афанасьева 01 марта 2011 г. Программа

Вид материала

Программа

Содержание Основные теоремы дифференциального исчисления и их приложения. Функции нескольких переменных. Неявные функции. Числовые ряды. Функциональные ряды. Кратные интегралы. Криволинейные интегралы. Поверхностные интегралы. Теория поля. Дисциплина: Функциональный анализ Метрические пространства. Мера и интеграл Лебега. Банаховы пространства. Гильбертовы пространства. Линейные интегральные уравнения. Дисциплина: Теория функций комплексного переменного Дисциплина: Алгебра, линейная алгебра и геометрия Дисциплина: Дискретная математика Булевы функции. Элементы теории графов. ... Полное содержание

Подобный материал:

• 9770     11-ая Международная конференция палеонтологов-радиоляристов (интеррад-11), 1342.18kb.
• Программа мероприятий 1 2 марта 2011 г. Всероссийский студенческий конкурс по политическому, 419.53kb.
• Учебник: Верещагина И. Афанасьева, 58.99kb.
• Афанасьева Елена Дмитриевна с докладом. Сколько времени нужно на доклад, 389.74kb.
• Правительства Республики Казахстан от 14 марта 2011 года №254 далее программа, 9.86kb.
• В сфере хозяйственной деятельности: Постановление Правительства РФ от 11 марта 2011, 106.04kb.
• План проведения конференции «антикоррозионная защита-2011»: 29 марта 2011 г., вторник, 70.87kb.
• «Хроматографические методы исследований в практике испытательных лабораторий» в период, 129.09kb.
• Рекомендации «круглого стола» на тему «О состоянии генофонда якутского скота и перспективах, 63.96kb.
• Приказ № от " " 2011 г. Программа духовно-нравственного развития, воспитания обучающихся, 299.29kb.

УТВЕРЖДАЮ

Директор ИМИ СВФУ

___________ В.И.Афанасьева

01 марта 2011 г.


Программа вступительного экзамена в магистратуру

по направлению 010100 «Математика»

Дисциплина: Математический анализ

Непрерывные функции. Непрерывность функции в точке и на множестве. Локаль­ные свойства непрерывных функций. Точки разрыва. Ограниченность функции, непре­рывной на отрезке. Существование наибольшего и наименьшего значений функции. Прохождение функции через все промежуточные значения. Равномерная непрерывность функции, непрерывной на отрезке. Непрерывность основных элементарных функций.

^ Основные теоремы дифференциального исчисления и их приложения. Теоремы Ферма и Ролля. Теорема Лагранжа о конечных приращениях. Локальная формула Тей­лора. Асимптотические разложения элементарных функций. Применения дифференци­альною исчисления к исследованию функций: признаки знакопостоянства, монотон­ность, экстремумы, выпуклость, точки перегиба, раскрытие неопределенностей.

^ Функции нескольких переменных. Евклидово пространство т измерений. Обзор основных метрических и топологических характеристик точечных множеств евклидова пространства. Функции нескольких переменных, пределы, непрерывность. Свойства не­прерывных функций. Дифференциал и частные производные функции нескольких пере­менных. Достаточное условие дифференцируемости. Непрерывность дифференцируемой функции. Частные производные высших порядков, дифференциалы высших порядков. Формула Тейлора для функций нескольких переменных, экстремум.

^ Неявные функции. Неявная функция, определяемая одним уравнением. Совокуп­ность неявных функций, определяемых системой уравнений. Вычисление производной неявных функций. Условный экстремум. Метод неопределенных множителей Лагранжа.

^ Числовые ряды. Сходимость и сумма числового ряда. Критерий Коши. Знакопостоянные ряды. Сравнение положительных рядов. Признаки сходимости Даламбера, Коши; интегральный признак сходимости. Знакопеременные ряды. Абсолютная и ус­ловная сходимости. Признак Лейбница.

^ Функциональные ряды. Поточечная сходимость, равномерная сходимость. Мажо­рантные признаки Вейерштрасса равномерной сходимости функционального ряда, тео­рема о непрерывности суммы ряда; теоремы о почленном дифференцировании и интег­рировании функциональных рядов.

Степенные ряды. Радиус и интервал сходимости степенного ряда; формула Коши-Адамара. Равномерная сходимость и непрерывность суммы степенного ряда. Почленное дифференцирование и интегрирование степенных рядов. Ряд Тейлора. Разложение ос­новных элементарных функций в степенные ряды. Применение рядов к приближенным вычислениям.

^ Кратные интегралы. Кратные интегралы Римана и их свойства. Приведение двой­ного интеграла к повторному. Приведение тройного интеграла к повторному. Замена переменных в двойном интеграле. Замена переменных в тройном интеграле. Геометриче­ские и механические приложения двойных и тройных интегралов.

^ Криволинейные интегралы. Простая гладкая(кусочно-гладкая) кривая. Длина дуги кривой. Криволинейные интегралы первого и второго родов и их вычисление. Формула Грина. Выражение площади плоской области с помощью криволинейного интеграла.

^ Поверхностные интегралы. Простая гладкая (кусочно-гладкая) двусторонняя по­верхность без особых точек. Площадь поверхности. Поверхностные интегралы первого и второго родов и их вычисления. Формула Остроградского. Выражение объема тела с помощью поверхностного интеграла.

^ Теория поля. Скалярное поле. Векторное поле. Градиент. Поток. Дивергенция. Циркуляция. Ротор.

Ряды Фурье. Тригонометрическая система и ее ортогональность. Тригонометри­ческий ряд Фурье. Поточечная сходимость тригонометрического ряда Фурье кусочно-гладкой на [ -; ] функции. Достаточное условие разложимости функции в тригономет­рический ряд Фурье.

ЛИТЕРАТУРА

1. Зорич В.А. Математический анализ. Т . 1, 2.

2. Кудрявцев Л.Д. Курс математического анализа. Т. 1, 2.

3. Демидович Б.П. Сборник задач и упражнений по математическому анализу.
^

Дисциплина: Функциональный анализ

Теория множеств. Действия над множествами, закон двойственности. Взаимное однозначное соответствие. Равные, эквивалентные множества. Счетные множества, не­счетные множества. Понятия мощности и континуум. Сравнение мощностей. Существо­вание множества со сколь угодно большой мощностью.

^ Метрические пространства. Метрика, сходимость, полнота, сепарабельность. Примеры метрических пространств. Теорема о вложенных шарах. Принцип сжатых отображений и его применения. Компактные множества. Необходимое и достаточное условия компактности в метрических пространствах. Свойства функций, заданных на компакте.

^ Мера и интеграл Лебега. Общие понятия о аддитивной меры. Измеримые функции и их структура. Интеграл Лебега. Связь интеграла Лебега с интегралом Римана. Неоп­ределенный интеграл Лебега. Восстановление функции по ее производной.

^ Банаховы пространства. Линейные нормированные пространства. Примеры. Изоморфность конечномерных линейных нормированных пространств 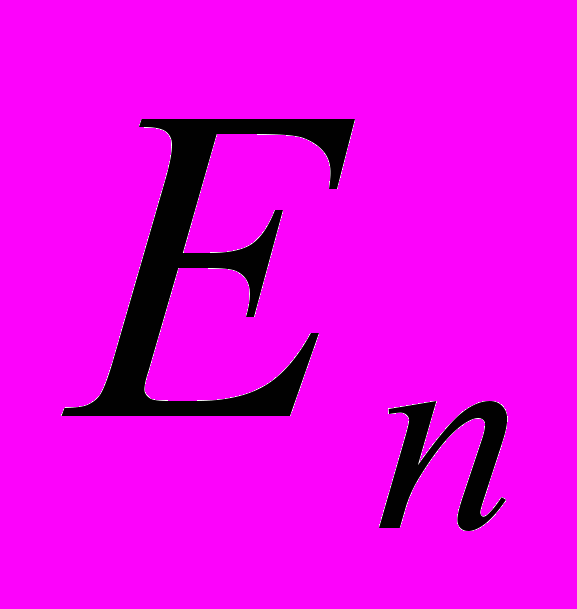п- мерному евклидову пространству 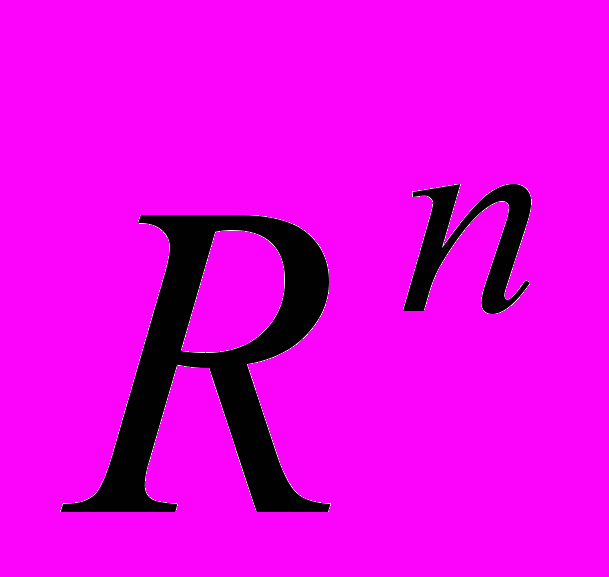. Нормируемость линейного топологического пространства. Линейные ограниченные операторы в банаховых пространствах. Ограниченность, нор­ма, непрерывность линейного оператора. Обратный оператор и его свойства. Компакт­ные операторы и уравнения с компактными операторами.

^ Гильбертовы пространства. Скалярное произведение, неравенство Коши-Буняковского, характеризация гильбертова пространства, Теорема Рисса-Фишера. Изо­морфизм сепарабельных пространств. Общий вид линейного функционала в гильбер­товом пространстве.

^ Линейные интегральные уравнения. Компактность интегральных операторов, тео­рема Фредгольма для уравнений с вырожденными ядрами. Уравнения Фредголъма с симметричными ядрами и теорема Гильберта-Шмидта.


ЛИТЕРАТУРА

1. Люстерник Л. А., Соболев В.И. Краткий курс функционального анализа.
   
2. Натансон И.П. Теория функций вещественной переменной.
   
3. Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа.
   

^ Дисциплина: Теория функций комплексного переменного

Комплексная плоскость. Комплексные числа. Кривые. Области.

Функции комплексного переменного. Понятие функции. Дифференцируемость функции в смысле действительного анализа и в смысле комплексного анализа. Понятие голоморфной функции

Дробно-линейная функция. Показательная функция.

Интеграл от комплексной функции. Вычисление интеграла по гладкой кривой. Теорема Коши (для односвязной области). Интегральная формула Коши. Интеграл Коши.

Ряд Тейлора. Теорема Тейлора. Неравенство Коши. Теорема Луивилля. Ряд Лорана. Теорема Лорана. Изолированные особые точки. Понятие целой и мероморфной функций.

Понятие вычета. Основ­ная теорема Коши о вычетах.

ЛИТЕРАТУРА

1. Шабат Б.В. Введение в комплексный анализ М.: Наука, 1976

2. Маркушевич А.И., Маркушевич Л.А. Введение в теорию аналитических функций М.: Просвещение, 1977


^ Дисциплина: Алгебра, линейная алгебра и геометрия


Однородные системы линейных уравнений (общее решение, фундаментальная система решений). Пространство решений. Связь решений неоднородной и соответствующей однородной систем линейных уравнений. Теорема Кронекера – Капелли.

Кольцо многочленов от одного неизвестного. Неприводимые многочлены в поле Р. Разложение в произведение неприводимых множителей. Основная теорема алгебры. Следствия. Формулы Виета. Рациональные корни целочисленных многочленов. Кратные корни. Теорема о кратных корнях.

Квадратичные формы. Приведение квадратичной формы к каноническому виду (основная теорема).

Группы. Теорема Лагранжа. Нормальные делители. Фактор – группы. Изоморфизм групп. Теорема Кэли.

Евклидовы действительные пространства. Процесс ортогонализации. Доказать, что ортогональное дополнение подпространства является подпространством. Представление Евклидова пространства в виде прямой суммы подпространства L и его ортогонального дополнения.


ЛИТЕРАТУРА

1. Курош А.Г. Курс высшей алгебры.
   
2. Скорняков Л.Я. Элементы алгебры.
   
3. Мальцев А.И. Основы линейной алгебры.
   

Дисциплина: Аналитическая геометрия и дифференциальная геометрия


Эллипс, гипербола, парабола, их изображение и их каноническое уравнение.

Определение поверхности вращения. Определение эллипсоида, однополостного гиперболоиды, эллиптического параболоида, их изображение и каноническое уравнение.

Определение кривой в дифференциальной геометрии. Определение и уравнение касательной к кривой, заданной параметрическими, неявными или явными уравнениями. Длина дуги кривой. Производные первого и второго порядков векторной функции и их геометрический смысл. Кривизна и кручение кривой. Определение сопровождающего трехгранника пространственной кривой.

Определение поверхности в дифференциальной геометрии. Определение и уравнение касательной плоскости к поверхности, заданной параметрическими, неявными или явными уравнениями.


ЛИТЕРАТУРА

1. Александров П.С. Лекции по аналитической геометрии.
   
2. Моденов П.С. Аналитическая геометрия.
   
3. Рашевский П.К. Курс дифференциальной геометрии.
   
4. Норден А.П. Краткий курс дифференциальной геометрии.
   
5. Моденов П.С., Пархоменко А.С. Сборник задач по аналитической геометрии.
   
6. Феденко А.С. Сборник задач по дифференциальной геометрии.
   

^ Дисциплина: Дискретная математика

Комбинаторика. Выборки. Перестановки. Сочетания. Перестановки с повторениями. Сочетания с повторениями. Число сочетаний. Число перестановок.

Перестановки данного состава. Полиномиальная формула. Производящие функции. Формула включений и исключений. Рекуррентные соотношения.

^ Булевы функции. Основные способы задания булевых функций. Существенные и фиктивные переменные. Формулы и эквивалентность формул. Элементарные функции. Разложение функций по переменным.

Полнота и замкнутость. Представление булевых функций полиномами Жегалкина.

Линейные функции. Принцип двойственности. Леммы о немонотонной, несамодвойственной, нелинейной функции. Теорема Поста.

^ Элементы теории графов. Графы. Основные понятия. Изоморфизм графов. Связность. Компоненты связности. Планарность.


ЛИТЕРАТУРА

1. Яблонский С.И. Введение в дискретную математику.
   
2. Гаврилов Г.П., Сапоженко А.А. Сборник задач по дискретной математике.
   

Дисциплина:^ Уравнения с частными производными


Приведение к каноническому виду и классификация линейных уравнений с частными производными второго порядка, характеристики. Вывод уравнений колебаний струны, теплопроводности, Лапласа. Постановка основных краевых задач, их физическая интерпретация.

Задача Коши для уравнения колебаний струны, формула Даламбера. Теоремы единственности и устойчивости решения задачи Коши. Метод Фурье для уравнения колебаний струны.

Принцип максимума в ограниченной области и единственность решения задачи Коши для уравнения теплопроводности. Построение решения задачи Коши для уравнения теплопроводности: формула Пуассона.

Уравнения Лапласа и Пуассона, фундаментальное решение уравнение Лапласа. Принцип максимума для гармонических функций. Функция Грина задачи Дирихле, решение задачи Дирихле для уравнения Лапласа в шаре.


ЛИТЕРАТУРА

1. Михайлов В.П. Дифференциальные уравнения в частных производных второго порядка. – М.: Наука, 1976
   
2. Ладыженская О.А. Краевые задачи математической физики. – М.: наука, 1973
   
3. Тихонов А.Н., Самарский А.А. Уравнения математической физики. - М.: Наука, 1977
   
4. Соболев С.Л. Уравнения математической физики. – М.: Наука, 1966
   
5. Бицадзе А.В. Уравнения математической физики. - М.: Наука, 1982
   

Дисциплина: ^ Дифференциальные уравнения.


Дифференциальные уравнения первого порядка. Частное решение. Общее решение, особое решение. Нахождение общего решения линейного дифференциального уравнения первого порядка.

Линейные дифференциальные уравнения n –го порядка. Фундаментальная система решений, общее решение линейного однородного уравнения. Структура общего решения линейного неоднородного уравнения. Метод Лагранжа для нахождения частного решения линейного неоднородного уравнения.

Линейные неоднородные уравнения n – го порядка с постоянными коэффициентами. Характеристическое уравнение, нахождение фундаментальной системы решений в зависимости от корней характеристического уравнения.

Линейные системы уравнений с постоянными коэффициентами. Характеристическое уравнение, фундаментальная система решений. Общее решение. Метод Лагранжа для нахождения частного решения линейной неоднородной системы уравнений.


ЛИТЕРАТУРА

1. Понтрягин. Л.С. Обыкновенные дифференциальные уравнения.
   
2. Матвеев Н.М. Методы интегрирования обыкновенных дифференциальных уравнений.
   
3. Тихонов А.Н., Васильева А.Б., Свешников А.Г. Дифференциальные уравнения.
   
4. Самойленко А.М., Кривошея С.А., Перестюк Н.А. Дифференциальные уравнения. Примеры и задачи.
   

Дисциплина: ^ Теория вероятностей

Пространство элементарных событий. Аксиомы теории вероятностей. Свойства вероятности. Условная вероятность. Независимость событий. Теорема умножения. Формула полной вероятности. Формулы Байеса. Схема Бернулли. Формула Бернулли. Теорема Пуассона. Локальная и интегральная теоремы Муавра-Лапласа. Случайная величина. Функция распределения вероятностей случайной величины и ее свойства. Плотность распределения вероятностей случайной величины и ее свойства. Основные дискретные и абсолютно непрерывные распределения. Математическое ожидание и дисперсия случайной величины, их свойства. Начальные и центральные моменты случайной величины. Неравенства Чебышева. Закон больших чисел: теорема Чебышева, теорема Бернулли. Характеристические функции. Центральная предельная теорема.


ЛИТЕРАТУРА

1. Гнеденко Б.В. Курс теории вероятностей. - М.: Наука, 2000.
   
2. Гихман И.И., Скороход А.В., Ядренко М.И. Теория вероятностей и математическая статистика. - Киев: Выща школа, 1988.
   
3. Вентцель Е.С. Теория вероятностей. – М.: Высшая школа, 1999.
   
4. Прохоров А.В., Ушаков В.Г, Ушаков Н.Г. Задачи по теории вероятностей: Основные понятия. Предельные теоремы. Случайные процессы. - М.: Наука, 1986.
   
5. Севастьянов Б.А. Курс теории вероятностей и математической статистики. М.: Наука, 1982.
   
6. Мынбаева Г.У. и др. Теория вероятностей в примерах и задачах. Учебное пособие. М.: Вузовская книга, 2005.
   

Дисциплина: Математическая статистика


Точечные оценки; свойства оценок: несмещенность и состоятельность; метод моментов; свойства выборочных моментов. Функция правдоподобия, неравенство Рао-Крамера, эффективные оценки, оценки максимального правдоподобия и их свойства. Интервальное оценивание: доверительные интервалы для математического ожидания и дисперсии нормально распределенной случайной величины. Гипотезы согласия, независимости, однородности; ошибки первого и второго рода; уровень значимости и мощность критерия; равномерно наиболее мощные критерии, лемма Неймана-Пирсона; критерии согласия хи-квадрат и Колмогорова; критерий однородности Смирнова-Колмогорова; критерии Вилкоксона и Стьюдента сравнения средних; критерий Фишера сравнения дисперсий. Выборочный коэффициент корреляции, свойства; проверка гипотезы о значимости выборочного коэффициента корреляции; метод наименьших квадратов, линейная регрессионная модель.


ЛИТЕРАТУРА

1. Боровков А.А. Математическая статистика. М.: Наука, 1984.
   
2. Бочаров П.П., Печинкин А.В. Математическая статистика. М.: Изд-во Ун-та дружбы народов, 1994.
   
3. Ивченко Г.И., Медведев Ю.И. Математическая статистика. М.: Высшая школа, 1984.
   
4. Колемаев В.А., Калинина В.Н. Теория вероятностей и математическая статистика. – М.: Высш.школа, 2003.
   

Дисциплина: Вариационное исчисление и методы оптимизации


Гладкие экстремальные задачи с ограничениями типа равенств и неравенств. Правило множителей Лагранжа. Седловая точка функции Лагранжа. Численные методы минимизации, градиентные методы. Задачи линейного программирования и проблемы экономики. Графический метод и симплекс-метод с естественным и с искусственным базисом. Двойственные задачи, основные теоремы двойственности. Задачи выпуклого программирования. Теорема Куна-Таккера. Классическое вариационное исчисление. Уравнение Эйлера-Лагранжа, различные обобщения. Задачи с ограничениями. Достаточные условия слабого и сильного экстремума (Лежандра, Якоби, Вейерштрасса). Задачи оптимального управления. Принцип максимума Понтрягина и метод динамического программирования Беллмана.

Литература

1. Алексеев В.М., Тихомиров В.М., Фомин С.В. Оптимальное управление.
   
2. Болтянский В.Г. Математические методы оптимального управления.
   
3. Васильева А.Б., Медведов Г.Н., Тихонов Н.А., Уразгильдина Т.А. Дифференциальные и интегральные уравнения. Вариационное исчисление.
   
4. Васильев В.В. 13 лекций по основам вариационного исчисления.
   
5. Евстигнеев В.Г. Вариационное исчисление.
   
6. Гельфанд И.М., Фомин С.В. Вариационное исчисление.
   
7. Моисеев Н.Н., Иванилов Ю.П., Столярова Е.М. Методы оптимизации.
   
8. Эльсгольц Л.Э. Дифференциальные уравнения и вариационное исчисление.
   
9. Алексеев Н.К. Задачи линейного программирования (учебно-методическое пособие). Якутск, ЯГУ.
   
10. Егоров И.Г. Задачи на максимум и минимум (учебное пособие). Якутск, ЯГУ.