Конспект лекций москва 2004 удк 519. 713(075)+519. 76(075) ббк 22. 18я7

Вид материала

Конспект

Содержание 6.4. Автоматы с -переходами Детерминизация автоматов с -переходами Оптимизация автоматов с -переходами

Подобный материал:

• Учебное пособие тверь 2008 удк 519. 876 (075. 8 + 338 (075. 8) Ббк 3817я731-1 + 450., 2962.9kb.
• Тексты лекций Москва 2008 удк 339. 9(075. 8) Ббк 65. 5я73-2, 1528.45kb.
• Программно-технический комплекс Учебное пособие Новочеркасск юргту (нпи) 2010. Удк, 3911.73kb.
• Удк 152. 27 (075. 8) + 157 (075. 8) + 152. 3 (075, 60.12kb.
• Краткий конспект лекций Кемерово 2002 удк: 744 (075), 1231.26kb.
• Методические указания по курсу Новосибирск 2004 ббк ю 937. 4 Удк 152. 26 (075), 802.63kb.
• Москва 2011 ббк 63. 3 (2)я 7 к 90 удк 947 (075) История России, 110.08kb.
• Курс лекций Гродно 2005 удк 631. 1 (075., 1193.16kb.
• Удк 070(075. 8) Ббк 76. 01я73, 5789.66kb.
• Удк 339. 9(470)(075. 8) Ббк, 7329.81kb.

6.4. Автоматы с -переходами

Автоматы с -переходами естественно возникают в различных приложениях и позволяют представить любой автомат в виде двухполюсников с одним входом и одним выходом, а так же строить сети из таких автоматов, сохраняя в них единственный вход и единственный выход. От рассмотренных ранее автоматов они отличаются тем, что в них присутствуют переходы, осуществляемые без чтения входной цепочки (на диаграмме такие переходы обозначаются стрелками, помеченными символом , рис.6).



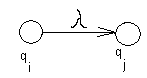
Рис. 6

Например, рассмотрим автомат с двумя выходами, представленный на рис. 7. Если просто объединить две выходные вершины автомата, то получившийся автомат не будет эквивалентен исходному, т.к. после построения символа b в результирующем автомате возможно будет построить символы а, что было невозможно в исходном автомате. Автомат, эквивалентный исходному, и являющийся двухполюсником, представлен на рис. 8.

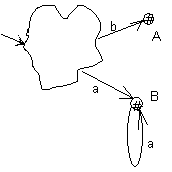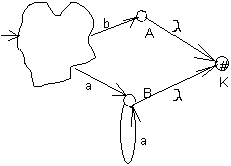Рис.7	Рис.8

Иногда в двухполюснике конечные состояния изображаются как .

Детерминизация автоматов с -переходами

Процедура детерминизации автоматов с -переходами задаётся следующей теоремой.

Теорема 4. Классы языков, допускаемых детерминированными автоматами и автоматами с -переходами, совпадают.

Доказательство.

Пусть автомат А = _T, q₀, F, K> – автомат с -переходами. Построим соответствующий детерминированный автомат А’= _T, q₀’, F’, K’>, такой, что L(A)=L(A’). Определим F’(q,a) и K’ следующим образом:

F’(q,a)={p / (q,ax) ├⁺ (p,x)}

K’ = K {q / (q, ) ├* ( p, )& pK}

Несложно показать, с использованием математической индукции по числу символов в распознаваемой цепочке, что получаемый таким образом автомат А’ переходит при распознавании цепочки x в конечное состояние тогда и только тогда, когда существует последовательность переходов в конечное состояние автомата А при распознавании этой же цепочки символов.

Очевидно, что если L – А-язык, то ему можно сопоставить некоторый двухполюсник.

Пусть языкам L₁ и L₂ сопоставлены соответствующие двухполюсники (рис.9,а). Тогда их объединению, конкатенации и итерации языка L₁ будут, соответственно, сопоставлены двухполюсники на рис. 9,б, 9,в и 9,г.



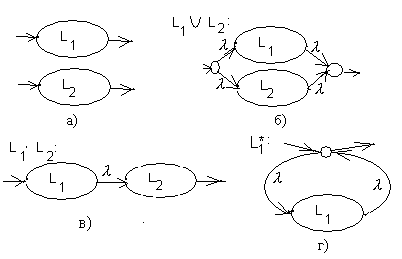
Рис.9


Сопоставляя доказанные ранее утверждения, получаем следующую теорему.

Теорема 5. Класс А-языков замкнут относительно операций объединения, конкатенации и итерации.

Оптимизация автоматов с -переходами

1. Если из состояния А исходит единственная дуга и это -дуга в состояние В, то вершины А и В можно слить.
   
2. Если из вершины А выходит -дуга в вершину В, являющуюся начальной вершиной некоторой дуги( не петли) или последовательности дуг, а С – конечная вершина этой дуги (последовательности дуг), и единственная дуга из С – -дуга в вершину А, то вершины А, В и С можно слить (примеры такого слияния приводятся на рис. 10 ( для одной дуги – а, б; для последовательности – в, г).
   

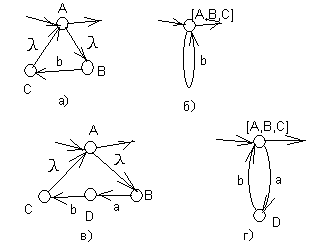
Рис.10

Пример. Пусть автомат S_B представлен диаграммой на рис. 11,а. Объединим по правилу 1 упрощения автоматов с -переходами состояния 4 и 5 и переобозначим состояния, как показано на рис. 11,б.



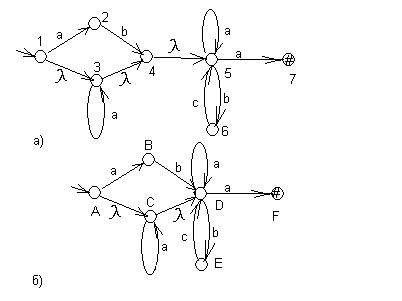
Рис.11

Построим функцию переходов детерминированного автомата S_B’.

F(A, a) = [B,C, D, F], F(A, b) = [E], F(A,c) = ,	F([B, C, D, F], a) = [C,D, F], F([B, C, D, F], b) = [D, E], F([B, C, D, F], c) = ,
F([E], a) = , F([E], b) = , F([E], c) = [D],	F([D, E], a) = [D, F], F([D, E], b) = [E], F([D, E],c) = [D],	F([D, F], a) = [D, F], F([D, F], b) = [E], F([D, F], c) = ,
F([D], a) = [D, F], F([D], b) = [E], F([D], c) = ,	F([C, D, F], a) = [C, D, F], F([C, D, F], b) = [E], F([C, D, F],c) =  .

Диаграмма детерминированного автомата S_B’ представлена на рис. 12. Для него K’ = { [B, C, D, F] , [ D, F], [C, D, F]}.



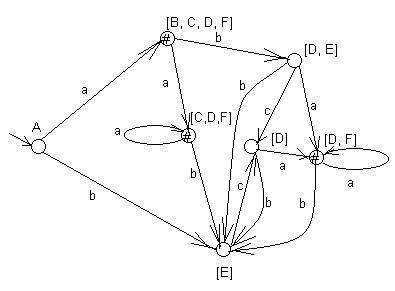
Рис.12

Тот же автомат после переобозначения состояний представлен на рис. 13.



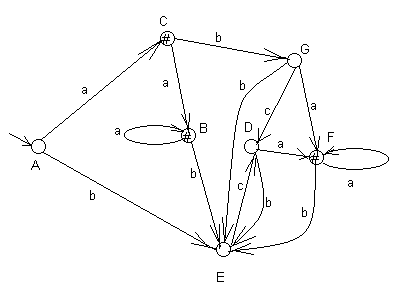
Рис.13