Geum.ru

Конспект лекций москва 2004 удк 519. 713(075)+519. 76(075) ббк 22. 18я7

Вид материалаКонспект

Содержание


12.3. Частичные автоматы
Подобный материал:
1   ...   13   14   15   16   17   18   19   20   21

12.3. Частичные автоматы


Автомат S называется частичным автоматом, если хотя бы одна из двух функций (F или G) не полностью определена, т.е. для некоторых пар (состояние, вход) значение F или G не определено (обозначается прочерками в таблице).

Состояния A и B называются псевдоэквивалентными (обозначается AB), если для них одновременно не определены или определены и равны функции F и G. Эти функции для частичных автоматов определяются следующим образом:

f(qi,)
  1. f(qi, aj) – по таблице переходов автомата
  2. если f(qi,) определена, то f(qi, aj)f(f(qi,),aj)
  3. если f(qi,) не определена, то не определена и f(qi, aj) для всех aj.

g(qi, aj)
    1. g(qi, aj) – по таблице автомата
    2. g(qi,  aj)  g (f(qi,), aj).
    3. Автоматное отображение:
    4. S(qi, aj)= g(qi, aj) (если g(qi, aj) не определено, то S(qi, aj) считаем равным прочерку)
    5. если f(qi,) определена, то S(qi, aj)=S(qi,) g(f(qi,) aj). Если g(f(qi,), aj) не определена, то считаем её равной прочерку)
    6. если f(qi,) не определена, то не определено и S(qi, aj) для всех aj.

Входное слово , для которого S(q0,) определено, называется допустимым для S.

Отметим неравноправность функций f и g – неопределенность g не препятствует допустимости слова, а неопределенность функции f для некоторого слова означает недопустимость любого его продолжения.

Состояния qi  S и rjT псевдонеотличимы (псевдоэквивалентны), если для любой цепочки  S(qi,)T(rj,) (т.е. области определённости и неопределённости для qi и rj совпадают, и в области определённости отображения совпадают).

Автоматы S и T псевдонеотличимы, если для любого состояния автомата S найдётся псевдонеотличимое от него состояние автомата T, и, наоборот, для любого состояния автомата T найдётся псевдонеотличимое от него состояние автомата S.

Для полностью определённых автоматов псевдонеотличимость совпадает с обычной неотличимостью.

Отношение псевдонеотличимости является отношением эквивалентности.

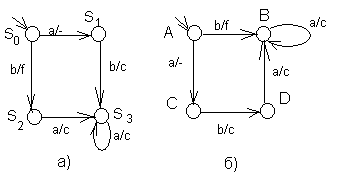
Пример псевдоэквивалентных автоматов приведён на рис.33 а,б.

Рис.33

Состояниям первого автомата соответствуют состояния: S0 – A, S1 – C, S2 – B и D, S3 – B, D; соответствия состояния второго автомата: A – S0, B – S3 и S2, C – S1, D – S2 и S3.

Недостаток введённого определения псевдоэквивалентности – необходимость совпадения областей определения. Можно дать эквивалентное определение, не требующее анализа совпадения областей: вводим новое, дополнительное состояние, переход в которое осуществляется при отсутствии перехода по данному входу, для которого переход по любому входу осуществляется в само себя, а в функции выхода прочерк будем рассматривать как дополнительную букву. Таким образом, автомат становится полностью определённым.

Минимизация не полностью определённых автоматов возможна двух типов: «строгая», с сохранением областей определения (что производится просто, как для доопределённого автомата), и через покрытия состояний, когда требуется совпадение переходов только в области определённости[3], здесь не рассматривается.

Если проводить строгую минимизацию, то автомат на рис. 33, а минимизируется до автомата, граф переходов которого приведен на рис. 34.



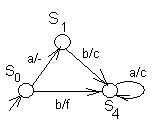
Рис. 34

Два основных аспекта работы автомата:
  1. Автоматы распознают входные слова, т.е. отвечают на вопрос М? (распознаватели)
  2. Преобразуют входные слова в выходные ( автоматные отображения):

Сравним эти аспекты работы автоматов. С одной стороны, последовательность ответов распознавателя на входные слова а1, а1а2, а1а2а3, … образуют выходное слово, которое является автоматным отображением; с другой стороны, выходные буквы можно разбить на два класса С1 и С2, и считать, что слово распознаётся, если g(q0,) С1. Таким образом, эти два представления автоматов являются эквивалентными.

Автомат может интерпретироваться как дискретное устройство, входная буква – входной сигнал, выходное слово – последовательность выходных сигналов.

Хотя с помощью автоматов может быть представлен достаточно широкий класс событий, существуют ограничения на вид событий, задаваемых автоматами, одно из них описывается в следующей теореме.

Теорема 23. Существуют события, не представимые в конечных автоматах: никакая непериодическая последовательность не распознаваема в конечных автоматах (например, последовательность 010110111011110111110…)

Доказательство.

Пусть непериодическая последовательность a1a2…aj… распознаётся автоматом S с n состояниями. Любой начального отрезок последовательности a1a2…aj также является допустимым, следовательно, f(q0,a1a2…aj)= qk Q1 (множество состояний, соответствующих допустимым цепочкам). При этом автомат проходит последовательность состояний из конечного множества Q1, значит, некоторое состояние встретится дважды: qs=qs+p. Это означает, что f(qs, as+1…as+p)=qs, поэтому периодическая последовательность также будет распознаваться автоматом, и, следовательно, непериодическая последовательность не может распознаваться конечным автоматом вопреки предположению.