Isbn 978-5-7262-1376 нейроинформатика 2011

Вид материала

Документы

Содержание Ключевые слова Постановка задачи Анализ уравнения в нулевом приближении Уточнение периода решения дифференциального уравнения Модель диффузионного взаимодействия Результаты компьютерного моделирования основной модели Список литературы

Подобный материал:

• Isbn 978-5-7262-1376 нейроинформатика 2011, 133.04kb.
• Isbn 978-5-7262-1376 нейроинформатика 2011, 164.77kb.
• Isbn 978-5-7262-1377 нейроинформатика 2011, 107.92kb.
• Isbn 978-5-7262-1375 нейроинформатика 2011, 127.94kb.
• Isbn 978-5-7262-1375 нейроинформатика 2011, 25.66kb.
• Isbn 978-5-7262-1375 нейроинформатика 2011, 105.62kb.
• Isbn 978-5-7262-1226 нейроинформатика 2010, 142.85kb.
• Isbn 978-5-7262-1377 нейроинформатика 2011, 136.96kb.
• Isbn 978-5-7262-1375 нейроинформатика 2011, 79.42kb.
• Isbn 978-5-7262-1226 нейроинформатика 2010, 136.25kb.

В.А. ШАБАРШИН

Ярославский государственный университет им. П.Г. Демидова

falemnderit@yandex.ru


АСИМПТОТИЧЕСКИЙ АНАЛИЗ УРАВНЕНИЯ

АЛЬТЕРНАТИВНОЙ МОДЕЛИ ИМПУЛЬСНОГО

НЕЙРОНА С ЗАПАЗДЫВАНИЕМ


В статье с помощью метода пошагового интегрирования проведено исследование периодического решения дифференциального уравнения и численно смоделировано диффузионное взаимодействие системы двух импульсных нейронов, описываемых дифференциальными уравнениями с запаздыванием.


Ключевые слова: уравнение Хатчинсона, метод пошагового асимптотического интегрирования, диффузионное взаимодействие


Введение


В настоящее время дифференциальные уравнения с запаздывающим аргументом находят большое применение в различных задачах прикладной математики. Дифференциальные уравнения с отклоняющимся аргументом встречались еще в работах Л. Эйлера, однако их теория была развита только в двадцатом веке. В 1948 году появилась модель численности популяции, предложенная Г.Е. Хатчинсоном. Модель основана на уравнении с запаздыванием 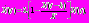где 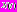– численность особей, – некоторый средний размер популяции (иногда называется емкостью среды), – показатель роста. В данной работе исследуется уравнение типа Хатчинсона.

В работе [1] для феноменологической импульсной модели нейрона: 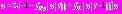основанной на дифференциальном уравнении с запаздыванием, проведена оценка нулевого приближения для периода решения. В работах [2] и [3] получена поправка к периоду. В [4] предложен новый метод асимптотического исследования дифференциальных уравнений с запаздыванием, описывающих динамику импульсного нейрона. Техника вычисления периода используется в данной работе при рассмотрении вопроса о существовании периодического решения уравнения с нелинейностью, удовлетворяющей определенным условиям.


Постановка задачи


Рассмотрим дифференциальное уравнение:

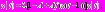(1)

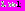
где – некоторая константа, 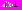Функция 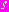– гладкая, относительно быстро и монотонно стремящаяся к нулю. Будем считать, что она удовлетворяет следующим условиям: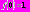

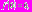
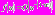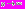при . (2)

Начальная задача отыскания решения уравнения (1) определяется заданием функции 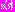на отрезке единичной длины. В работе будем использовать отрезок 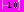. Определим множество 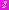– класс непрерывных функций: 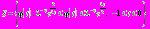В качестве начальной функции для (1) будем выбирать произвольную функцию 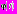из класса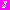

С помощью метода пошагового интегрирования требуется провести исследование периодического решения дифференциального уравнения, получить оценку периода, провести численное исследование системы двух импульсных нейронов, описываемых дифференциальными уравнениями с запаздыванием.


Анализ уравнения в нулевом приближении


Мы рассматриваем дифференциальное уравнение (1) с функцией 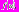удовлетворяющей условиям (2). Пусть начальная функция 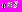Введем оператор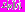 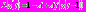. Перепишем уравнение (1) в виде: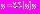

1. Рассмотрим промежуток 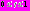(соответственно )

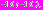На этом промежутке функция – решение уравнения – растет очень быстро и достигает максимального значения. В точке 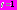происходит как бы переключение: до 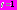функция росла, а после этого момента времени начинает падать. При 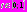функция 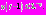Функцию 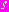представим в виде: 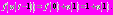В таком случае оператор 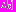принимает вид: 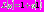, а уравнение (1) 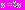Его решение: Находим его значение в граничной точке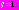

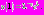
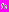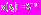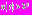2. Далее меняется от 1 до некоторого момента времени такого, что При таких выполняются следующие неравенства: и 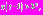т.е. обе функции принимают очень большие значения. В этом случае 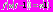Оператор 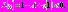так как больше единицы. Значения оператора отрицательны, значит производная тоже отрицательная. На этом промежутке времени значения функции убывают до порогового значения 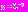Причем переключения не происходит: на этом участке функция 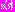– монотонная (строго убывающая). Исходное уравнение принимает вид: 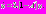Его решение есть функция 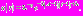Вспомним, что 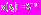Одновременно, Выразим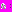

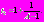
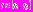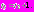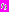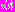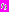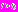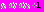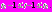3. Перейдем к следующему промежутку: , где До момента времени функция по-прежнему убывала. В точке произойдет «переключение»: при решение начинает вновь расти. Так как сейчас то В этом случае 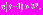Мы попали в ситуацию, аналогичную рассмотренной в пункте 2. Тогда решение уравнения (1) имеет вид: 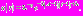Найдем, чему равна эта функция на конце рассматриваемого промежутка: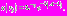

4. Пусть 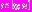, где момент времени 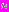таков, что 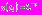На этом отрезке времени функция растет до порогового значения 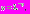и мы оказываемся в ситуации первого промежутка. Здесь справедливы следующие неравенства: 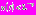и 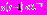Функция 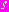раскладывается по формуле Тейлора в такую сумму: 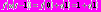. Оператор 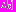переписывается таким образом: 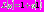. Уравнение (1) принимает следующий вид: 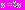Его решение таково: 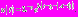В точке 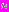решение исходного уравнения: 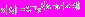В то же время, 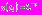Выразим момент времени .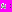

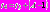Ниже приведены значения для основных моментов времени:

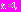
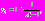
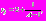
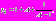
Для того чтобы продолжить построение асимптотики для моментов времени 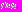заметим, что в этом случае функцию на последнем промежутке следует рассматривать как новую начальную функцию уравнения (1). Она входит во множество допустимых начальных функций и, построив для нее асимптотическое решение на промежутке 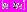, мы убедимся, что очередная начальная функция удовлетворяет определению класса начальных функций. Таким образом, для произвольной начальной функции 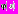построенная асимптотика оказывается периодической функцией с периодом, равным .


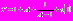Уточнение периода решения дифференциального уравнения

с запаздыванием


Вернемся к рассмотрению дифференциального уравнения (1), и проведем рассуждение, аналогично работам [2]–[4], которое позволит нам уточнить значение периода.

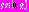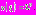1. Рассмотрим промежуток , где Соответственно, 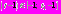. Поэтому 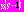мало, и функцию 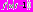можно разложить по формуле Тейлора в точке 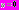по степеням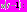 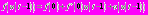. Аргумент 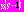функции 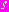равен 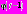. Учитывая, что функция 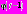принадлежит классу 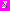удовлетворяющему формуле (6), и 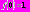формулу для 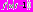перепишем как: 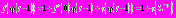. Тогда уравнение (1) приобретает следующий вид: 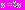Его решение 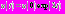. Подставим значение 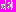, получим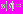 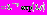. В точке 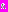значение функции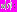 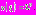Отсюда 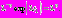Выразим момент времени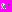

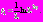
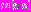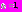2. Далее меняется на промежутке , где и 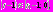т.е. по-прежнему 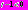Повторяя рассуждения предыдущего пункта и учитывая начальное значение 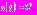запишем решение уравнения на втором промежутке: 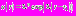. Отсюда при .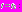

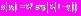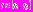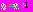3. Рассмотрим отрезок времени , где Тогда 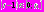. Уравнение (1) имеет вид: 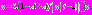Запишем его решение: 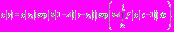Найдем значение функции при 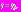Используя рассуждения в работе [1], получим, что 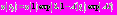, где .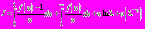

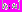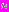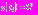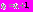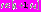4. В качестве четвертого промежутка для построения решения выберем интервал , где момент времени определяется из условия Так как то и 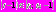. При таких значениях аргумент запаздывающей функции 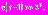Поэтому 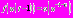. Следовательно, уравнение имеет вид: 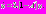Решением является функция: 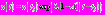. Зная, что 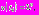найдем момент времени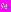

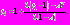
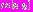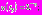5. На следующем шаге , где соответственно 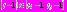, и 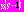по-прежнему велико. Поэтому функция 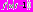мала, и уравнение сохраняет вид, как в предыдущем пункте. Решением является функция 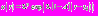. Определим 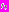из условий промежутка: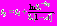

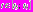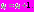6. Пусть теперь , где Тогда 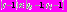, т.е.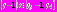, и значения функции 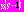все еще велики. Решение исходного уравнения на этом промежутке: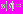 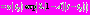. Найдем значение функци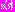и при .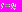

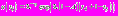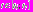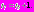7. Сейчас , где Соответственно, .

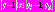Решение уравнения (1) имеет вид:

.

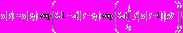Значение решения дифференциального уравнения (1) в момент времени 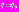имеет вид (используется подход, описанный в работе [1]) .

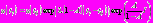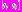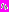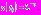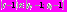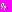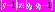8. Рассмотрим промежуток , для которого момент времени определен условием Тогда, . Если учесть, как определялся момент то . Значение функции 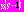здесь очень мало, и уравнение (1) принимает в таком случае вид: 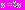Его решение: 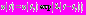. Значение в момент времени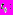 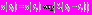. Найдем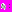



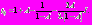
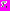
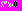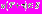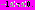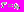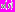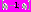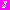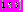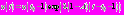Мы хотим показать существование такого промежутка времени что для Тем самым будет определено наличие периодического решения уравнения (1). Чтобы утверждать, что нужно убедиться в том, что значения функции на промежутке принадлежат множеству Это так, если параметр выбран из промежутка . Значение решения для таких определяется . Таким образом, доказана следующая теорема.

Теорема. Пусть функция 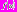определена для положительных значений аргумента, непрерывно дифференцируема и положительна, монотонно убывает, при 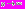ведет себя как 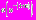. Функция удовлетворяет условиям 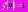и 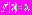Тогда уравнение (1) с начальными условиями из множества 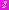имеет периодическое решение и период определяется формулой 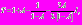где .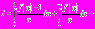


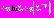Модель диффузионного взаимодействия


Биологический нейрон – это биологическая клетка, выполняющая функции, связанные с генерированием электрических импульсов, т.е. нелинейная электрическая система. К настоящему моменту времени существует множество самых разнообразных математических моделей нейрона. Следуя работам [1] и [4] мы будем рассматривать дифференциальное уравнение (1) как уравнение, описывающее динамику мембранного потенциала нейрона. Рассмотрение множества одинаковых взаимодействующих нейронов приводит к понятию нейронной сети. Именно моделирование сетей представляет основной интерес. Важная характеристика нейронной сети – механизм взаимодействия ее элементов. Для моделирования взаимодействия в правую часть уравнения нейрона-приемника добавим слагаемое, которое соответствует току проводимости. 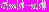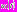Значение этого слагаемого определяется разностью мембранных потенциалов взаимодействующих нейронов: , где и 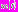– мембранные потенциалы этих нейронов. Параметр 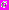имеет смысл коэффициента разностной диффузии. В работе [1] приведены биологические соображения о том, что коэффициент разностной диффузии 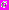мал по величине и согласован с параметром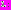 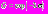, где 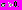В этом случае в системах, состоящих из электрически взаимодействующих импульсных нейронов, имеют место разнообразные типы синхронизации колебательных режимов. Нейронная сеть, состоящая из импульсных нейронов с электрическим взаимодействием, будет описываться следующей системой уравнений:

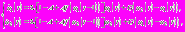(3)

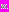где и 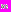– мембранные потенциалы взаимодействующих нейронов, а 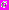– коэффициент проводимости межклеточной жидкости.


Результаты компьютерного моделирования основной модели


Было проведено численное решение уравнения (1) и системы (3) с помощью формулы прямоугольников. Поскольку нас интересуют импульсные решения, то параметр 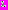выбран так, чтобы было выполнено неравенство 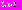На рис. 1 приведен график решения уравнения (1) на интервале 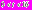при 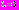(численное интегрирование проводилось с шагом 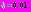На рис. 2 изображен график решения системы (3) пр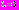и и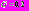



Рис. 1. Решение уравнения (1) при  = 3




Рис. 2. Решение системы (3) пр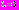и и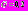

Заключение


В работе проведено исследование дифференциального уравнения (1), которое описывает динамику мембранного потенциала нейрона-пейсмейкера. В качестве начального условия была выбрана начальная функция из соответствующего класса, затем уравнение решалось методом шагов. Доказано существование периодического решения у соотношения, и выведена формула для вычисления значения этого периода. Для компьютерного эксперимента была написана программа. Она позволяет решить численно уравнение (1) и систему уравнений (3) и построить эти решения. Работа имеет хорошую перспективу развития, например, для аналитического исследования задачи взаимодействия нейронов.


Список литературы


1. Кащенко С.А., Майоров В.В. Модели волновой памяти. М.: Книжный дом ЛИБРОКОМ, 2009, 288 с.

2. Майоров В.В., Мячин М.Л., Парамонов И.В. Поправка к периоду решения уравнения, моделирующего динамику мембранного потенциала нейрона. // Моделирование и анализ вычислительных систем. Т. 15, № 2. / Под ред. В. А. Соколова. Ярославль: Изд-во Яросл. гос. ун-та им. П. Г. Демидова, 2008. С. 61–66.

3. Дунаева О.А., Мячин М.Л. Исправления и дополнения к статье «Поправка к периоду решения уравнения, моделирующего динамику мембранного потенциала нейрона». // Моделирование и анализ вычислительных систем. Т. 16, № 3. / Под ред. В.А. Соколова. Ярославль: Изд-во Яросл. гос. ун-та им. П.Г. Демидова, 2009. С. 58–64.

4. Мячин М.Л. Исследование автоколебательных режимов в сетях импульсных нейронов: дис. … к. ф.-м. наук : 05.13.18 // Мячин М. Л. Ярославль, 2009. 85 с.