Geum.ru

Дипломная работа на тему: Группы самосовмещений

Вид материалаДиплом

Содержание


В первой главе даются основные понятия теории групп, рассматриваются виды групп самосовмещений геометрических фигур, группы опер
В третьей главе дается определение орнаментов и пакетов, и их полная классификация
Глава I. Группы самосовмещений
G будет выполняться: . Подмножество Н
Н, есть элемент множества H
Теорема Силова.
М – произвольная часть группы G
Подобный материал:


Дипломная работа на тему:


Группы самосовмещений

геометрических фигур на плоскости

и в пространстве


План

Стр.

Введение ………………………..………………………………..……..
3

Глава I. Группы самосовмещений геометрических фигур

на плоскости ………………………………………………………….....



§1. Простейшие понятия теории групп ……………………………
5

§2. Группы самосовмещений простейших геометрических фигур




Глава II. Орнаменты и паркеты ……………………………………



§1. Орнамент и его группа симметрии …………………..………



§2. Паркеты и мозаики ..…………………………………..………



Глава III. Группы самосовмещений геометрических фигур

в пространстве ………………………………………….……………



§1. Группа самосовмещений тетраэдра ……………………………



§2. Группа самосовмещений куба …….……………..……………



§ 3. Группа поворотов икосаэдра и додекаэдра …………………..



§4. Группы в кристаллографии …………………………………….



§5. Задачи на группы самосовмещений ………………………….



Заключение ……………………………………………………………


Литература ………..……………………………………………..……





Введение

Математика XXI века может сильно отличаться от нашей; возможно школьник начнет изучение алгебры с теории групп подстановок, что он мог бы сделать сейчас, если бы не установившиеся традиции.

Саймон Ньюкомб, 1893 г.


Чтобы выработать понятие группы в его современной форме, математикам потребовалось почти 100 лет. Двести лет назад знаменитый французский ученый Жозеф–Луи Лагранж (1936–1813), изучая решение алгебраических уравнений в радикалах, оперировал фактически с понятием “группа”, хотя и не пользовался самим этим термином. Им была сформулирована и доказана в 1771 году первая существенная теорема в теории групп.

Исследования Лагранжа продолжили норвежский математик Нильс Хенрик Абель и француз Эварист Галуа, которые впервые ввели термин “группа”. Элементами рассматриваемых ими групп были подстановки корней алгебраического уравнения

.

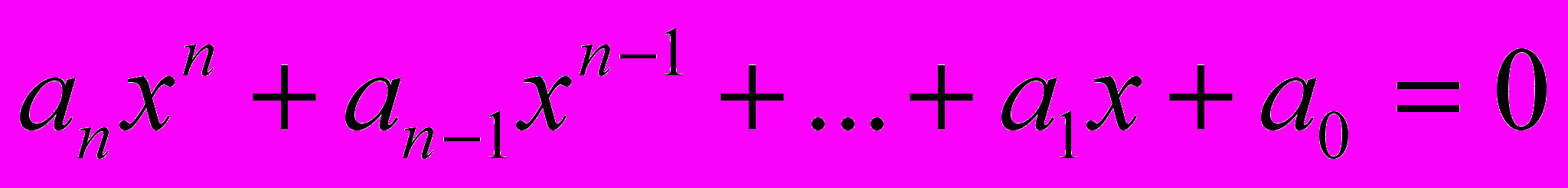Группы подстановок изучали также Огюстен–Луи Коши (1789–1903), Камилл Жордан (1838–1922) и другие известные математики. Принятое ныне определение группы было предложено Кэли в 1854 году.

С понятием группы тесно связано широко распространенное в природе свойство симметрии. Симметричны не только снежинки, пчелиные соты, кристаллы поваренной соли и кварцы. Элементарные частицы тоже подчиняются “закону симметрии” – зарядовому сопряжению, согласно которому каждой частице соответствует античастица. Проявлением симметрии окружающего нас мира являются принцип относительности Галилея, законы сохранения энергии.

Изучение закономерностей симметрии, общих для самых различных ее проявлений, и привело к созданию специального математического аппарата, называемого теорией групп.

Понятие группы на сегодняшний день, наряду с понятием функции, относится к самым фундаментальным понятиям всей математики. Оно позволяет в точных терминах охарактеризовать симметричность той или иной геометрической фигуры. Именно с таких позиций Е.С. Федоров (1891) решил задачу классификации правильных пространственных систем точек, являющуюся одной из основных задач кристаллографии.

В настоящее время теория групп является одной из самых развитых областей алгебры, имеющей многочисленные применения как в самой математике, так и за ее пределами – в топологии, теории функций, кристаллографии, квантовой механики и других областях математики и естествознания.

Целью моей дипломной работы является изучение отдельных видов групп самосовмещений геометрических фигур – определение структуры подгрупп, их изоморфизмы и гомоморфизмы.

Дипломная работа состоит из введения, трёх глав, приложения, заключения и списка используемой литературы.

В первой главе даются основные понятия теории групп, рассматриваются виды групп самосовмещений геометрических фигур, группы операций.

Во второй главе рассматривается применимость самосовмещений фигур на практике.

В третьей главе дается определение орнаментов и пакетов, и их полная классификация

В приложении приводится несколько картин – орнаментов голландского художника М. Эшера.

Глава I. Группы самосовмещений

геометрических фигур на плоскости


§1. Основные понятия теории групп


Множество, в котором задана одна или несколько алгебраических операций, называется алгебраической системой.

Общая алгебраическая теория операций, или, общая теория алгебраических систем распадается на ряд отдельных направлений, каждое из которых посвящено изучению алгебраических систем, в которой операция обладают той или иной системой свойств. Среди различных таких типов алгебраических систем некоторые выделяются в виду своей особой важности, и им обычно присваиваются особые наименования.

Множество, в котором задана ассоциативная операция, называется полугруппой. Данное понятие выкристаллизовалось и получило признание значительно позже, чем понятие группы. Однако группа является частным видом полугруппы.

Определение группы I. Множество, в котором задано ассоциативная операция, обладающее свойством обратимости, называется группой.

Определение группы II. Множество G с определенной на нем бинарной операцией * называется группой, если выполняются три аксиомы:

Аксиома 1. (существование единичного элемента).

Существует единичный элемент е во множестве G такой, что e*a = a*e = a, для любого элемента a из G.

Аксиома 2. (существование обратного элемента).

Для каждого элемента a множества G существует в G единственный элемент a-1 такой, что a*a-1 = a-1*a = e.

Аксиома 3. (ассоциативность бинарной операции).

Для любой тройки a, b, c элементов из G выполняется равенство: a*(b*c)= =(a*b)*c.

Пусть в группе G кроме трех изложенных выше аксиом выполняется еще одно условие: a*b = b*a. В этом случае группа G называется коммутативной или абелевой группой (в честь известного норвежского математика Н.Х. Абеля (1802–1829)).


Отображение группы G(*) и G'(*) называется гомоморфным, если для любых двух элементов a и b группы G(*) будет выполняться условие: .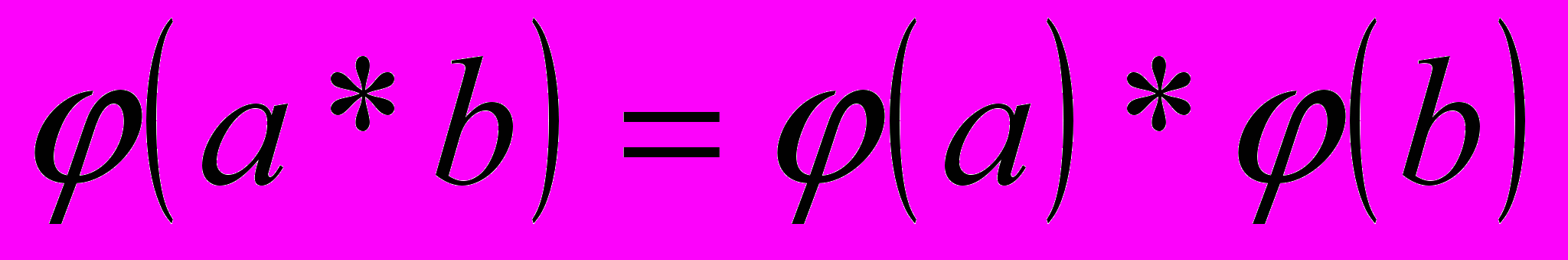

Группы G(*) и G'(*) называются изоморфными, если существует биективное отображение группы g(*) на группу G'(*), ‘сохраняющее операции’, то есть такое, что для любых 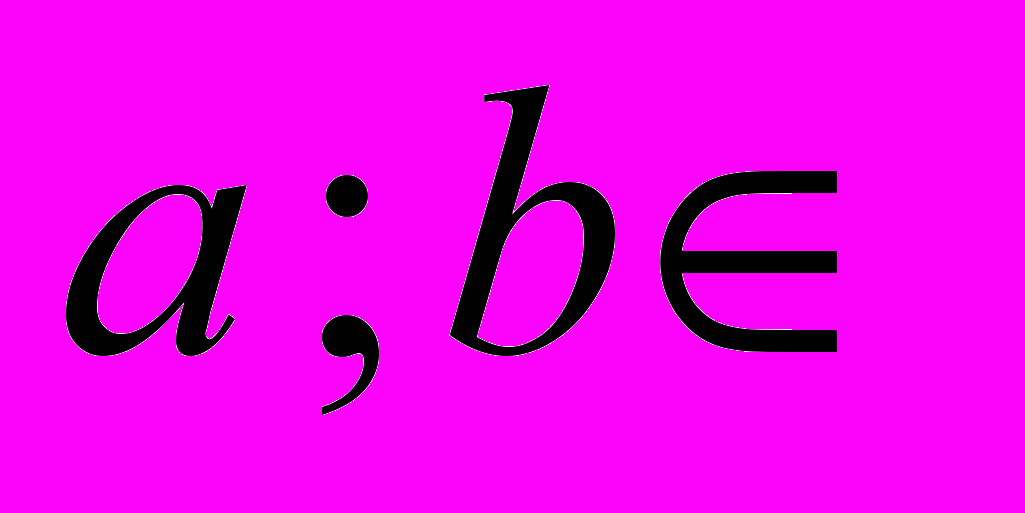G будет выполняться: .

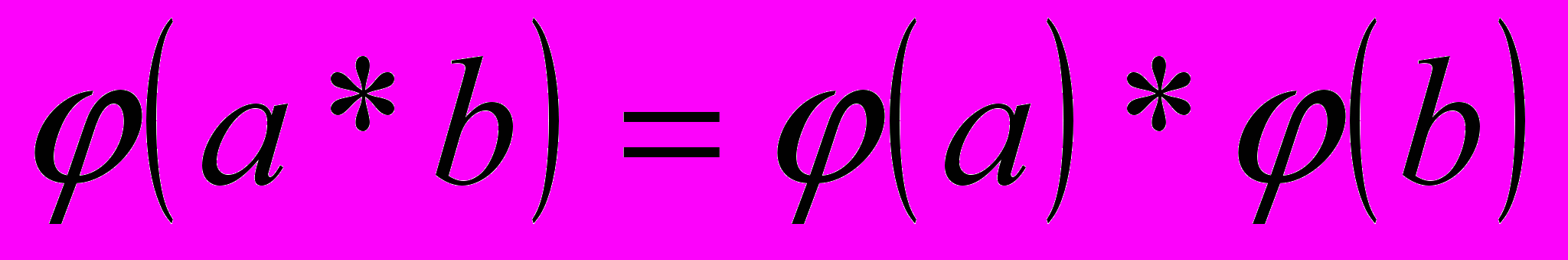Подмножество Н группы G называется подгруппой группы G, если оно само является группой относительно операции, определенной в группе G. Обозначение: Н ≤ G. Если Н ≤ G и Н ≠ G, то используется обозначение Н < G.

Признак подгруппы. Подмножество Н группы G тогда и только тогда является подгруппой группы G, если выполнены следующие условия:

1. Если aН и bH, то a*bН.

2 Единичный элемент группы G есть элемент множества Н.

3 Элемент, обратный к какому–нибудь элементу множества Н, есть элемент множества H.

Группа <G,·>, содержащая такой элемент a, что каждый элемент g из G является степенью a (т.е. g = an, для любого 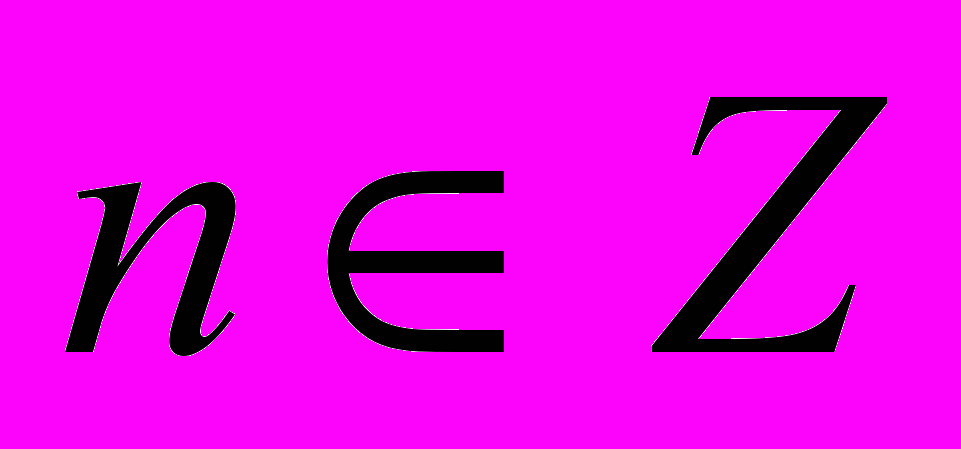), называется циклической с образующим a. Циклическая группа абелева.

Группа называется конечной, если она состоит из конечного числа элементов; в противном случае она называется бесконечной.

Число элементов конечной группы называется ее порядком.

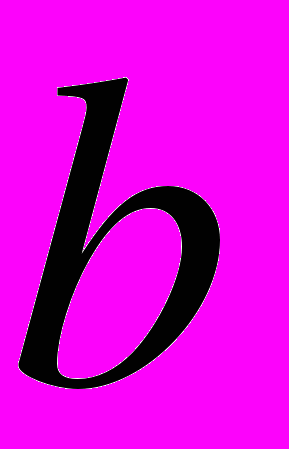Элементы и группы 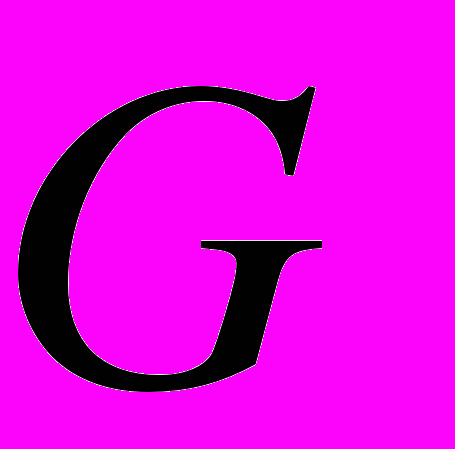называются сопряженными в этой группе, если в 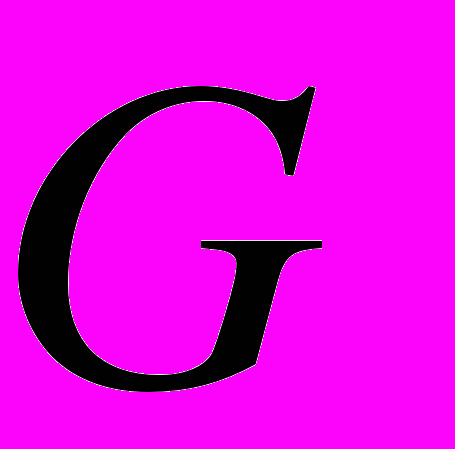можно найти хотя бы один такой элемент 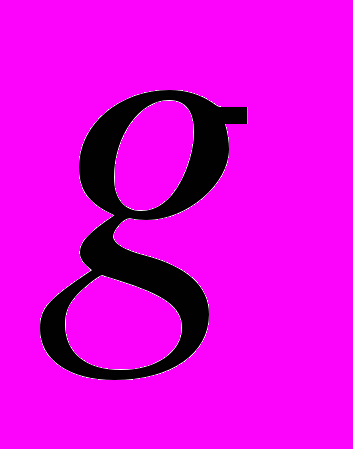, что 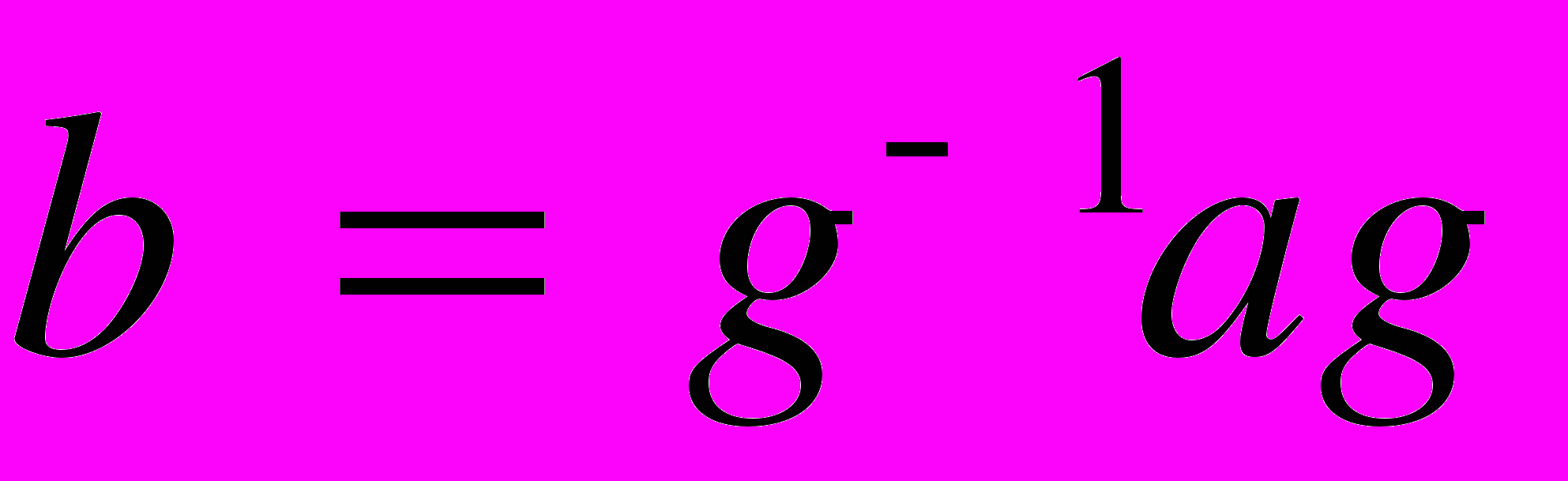. Бинарное отношение сопряженности является отношением эквивалентности, поэтому все множество элементов группы разбивается на классы эквивалентных элементов.

Для конечных групп имеют место утверждения:

1) Порядок k любого элемента конечной группы G является делителем порядка этой группы (теорема Лагранжа).

2) В конечной группе G порядка n для любого a справедливо an = e.

3) порядок конечной группы делится на наименьшее общее кратное порядков её элементов.

Теорема Силова. Пусть G – конечная группа, p – простое число.

П1. Существование. Для каждой степени p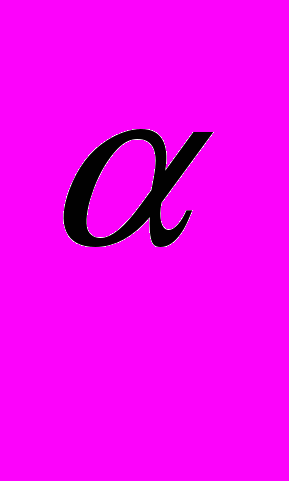, делящей порядок G, в G существует подгруппа порядка p.

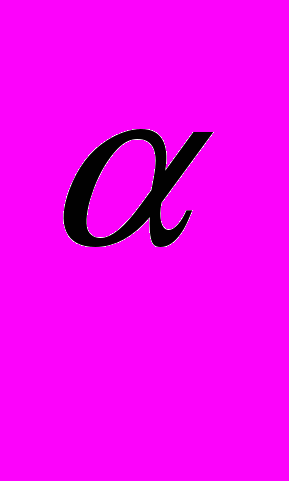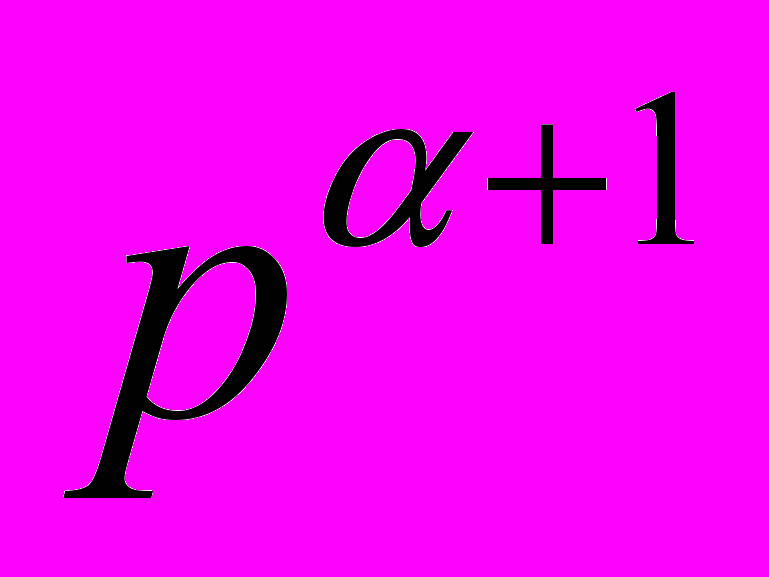
П2. Вложение. Если делит порядок G, то каждая подгруппа порядка p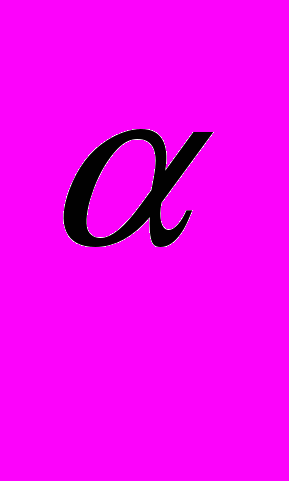 из G вложена в некоторую подгруппу порядка 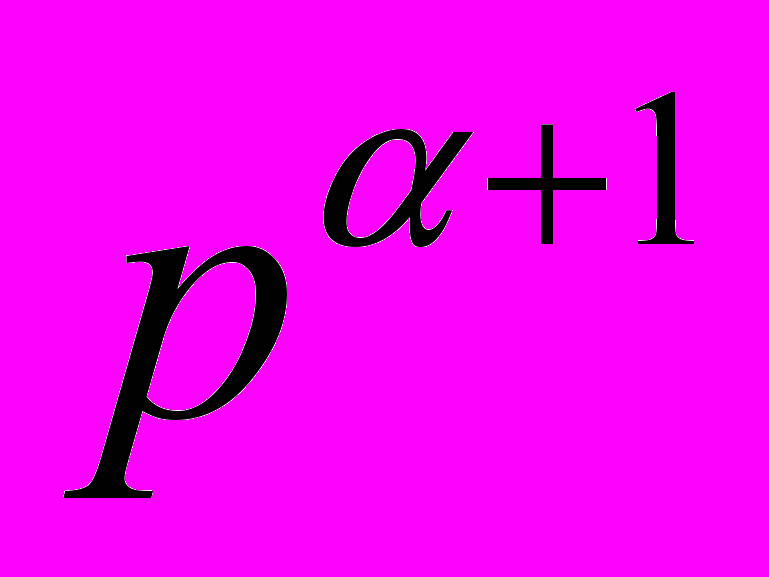из G. В частности, максимальные p-подгруппы из G – это в точности подгруппы порядка pr – максимальная степень p, делящая порядок G.

П3. Сопряжённость. Все максимальные p-подгруппы из G сопряжены в G.

П4. Количество. Количество максимальных p-подгрупп из G сравнимо с 1 по модулю p и делит порядок G.

Следствие. В конечной группе G порядка n, где n = 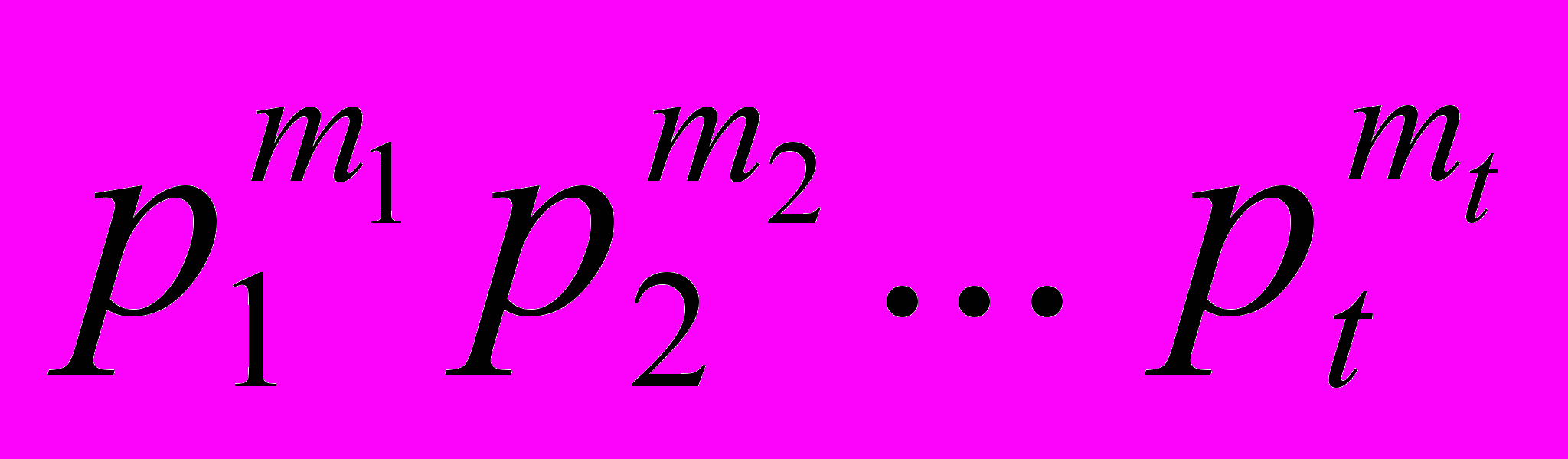имеются подгруппы порядков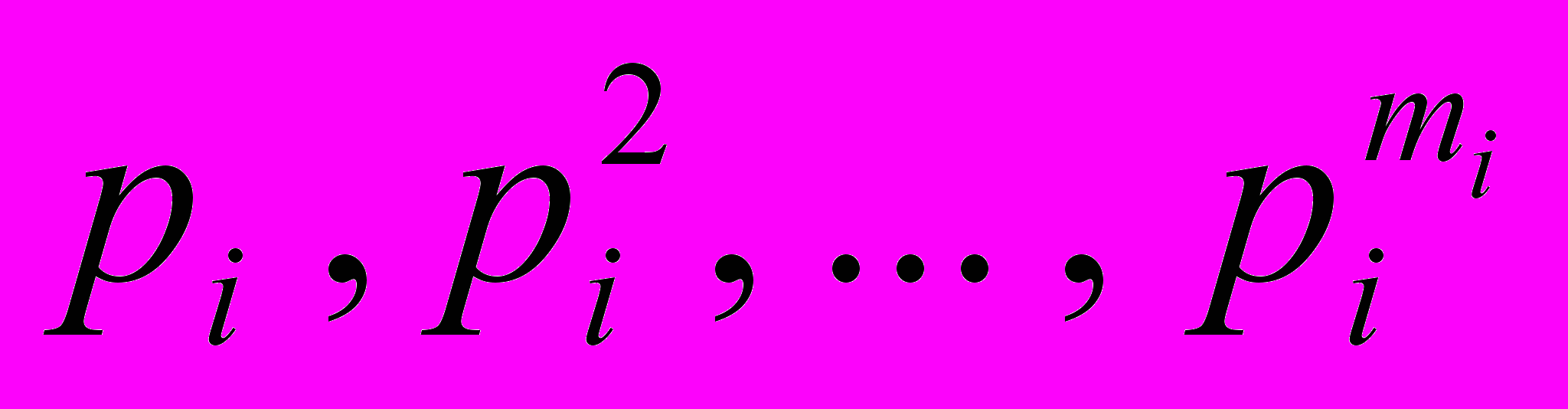для любого i = 1, 2, … , t.

Пересечение любого множества подгрупп само является подгруппой.

Если М – произвольная часть группы G, то пересечение [М] всех подгрупп, содержащих М, называется подгруппой, порожденной множеством М, а само М – порождающим множеством подгруппы [М]. Имеет место теорема:

[М] = .

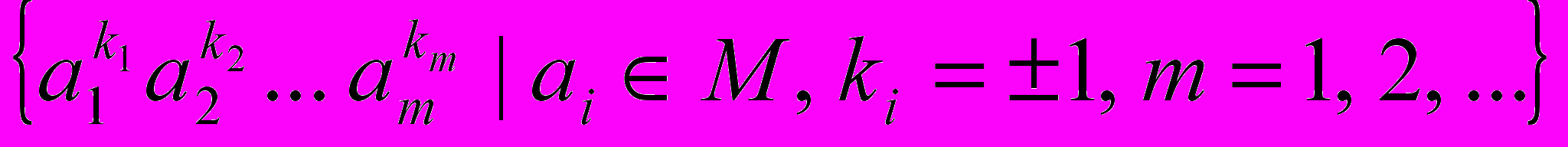Известно [14, 18, 20], что симметрическая группа Sn всевозможных подстановок n элементов порождается своими транспозициями (ij), т.е. подстановками вида 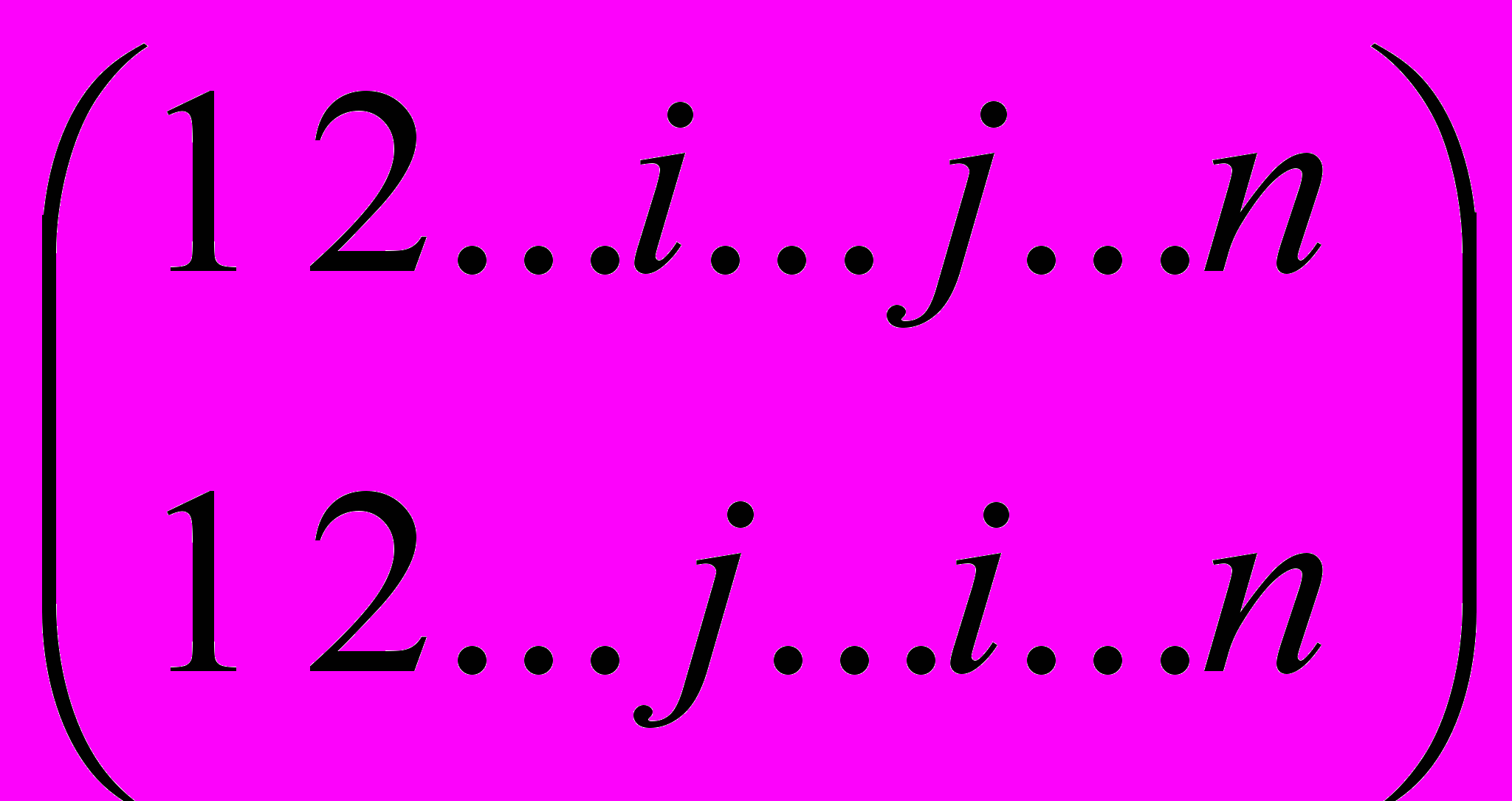, в i которых переходит в j, j – в i, а остальные элементы остаются на месте.

Однако (ij) = (1i)(1j)(1i), поэтому Sn порождается даже транспозициями вида (12), (13), … , (1n).

Знакопеременная группа An четных подстановок порождается всевозможными тройными циклами (ijk), т.к. четная подстановка является произведением четного числа транспозиций и

(ij) (ik) = (ijk), (ij) (kl) = (ilj) (jkl).

Антиподом порождающих множеств является подгруппа Фраттини. Чтобы прийти к этому понятию, назовем подгруппу Н группы G максимальной среди подгрупп со свойством ρ, если Н < G и не существует подгруппы Н′ с условием Н < Н′ < G и со свойством ρ. Если свойство ρ таково, что им обладают все группы, то подгруппы, максимальные среди подгрупп со свойством ρ, называются просто максимальными. Подгруппа Фраттини Ф(G) группы G – это пересечение всех ее максимальных подгрупп, если они существуют, и сама G – в противном случае. Элемент g группы G называется непорождающим элементом группы, если его можно удалить из любого порождающего множества группы G, в которое он входит.


Литература

  1. Александров П.С. Введение в теорию групп. – М.: Наука, 1980.
  2. Ван дер Варден Б.Л. Алгебра. – М.: Наука, 1976.
  3. Варпаховский Ф.Л., Солодовников А.С., Стеллецкий И.В. Алгебра. – М.: Просвещение, 1978.
  4. Вейль Г. Теория групп и квантовая механика. – М.: Наука, 1986.
  5. Гарднер М. Путешествие во времени. – М.: Мир, 1980.
  6. Гильберт Д., Кон–Фоссен С. Наглядная геометрия. – М.: Наука, 1981.
  7. Дальма А. Эварист Галуа, революционер и математик: Пер. с франц. – 2–е изд. – М.: Наука, 1984.
  8. Долбилин Н. Самоподобные мозаики // Квант. – 1998 – №2. – с.34–38.
  9. Дужин С.В., Чеботаревский Б.Д. От орнаментов до дифференциальных уравнений. Попул. введение в теорию групп преобразований – Минск, Высш. шк., 1988 , т.13: ил.; (мир занимательной науки).
  10. Засловский А. Паркеты и разрезания // Квант. –1999. – №2.– С.21–24.
  11. Земляков А. Орнаменты // Квант. – 1977. – с. 18–25.
  12. Калужнин Л.А., Сущанский В.И. Преобразования и перестановки. 2–е изд. – М.: Наука, 1985.
  13. Каплун В., Лейбович В., Папернов Е. Конечные паркеты // Квант. – 1972 – № 10 – с. 10–11.
  14. Каргаполов М.И., Мерзляков Ю.И. Основы теории групп. – М.: Наука. – 1972.
  15. Колмогоров А. Паркеты из правильных многоугольников // Квант.–1970. –№3 – С.15–17.
  16. Кострикин А.И. Введение в алгебру. – М.: Наука, 1977.
  17. Куликов Л.Я. Алгебра и теория чисел. – М.: Высшая школа, 1979.
  18. Курош А.Г. Курс высшей алгебры. – М.: Наука, 1975.
  19. Курош А.Г. Лекции по общей алгебре. – М.: Наука, 1973.
  20. Курош А.Г. Теория групп. 3–е изд. – М.: Наука, 1967.
  21. Любарский Г.Я. Теория групп и ее применение к физике. – М.: Гостехиздат, 1958.
  22. Ляпин Е.С., Лесохин М.М., Айзенштат А.Я. Упражнения по теории групп. – М.: Наука, 1967. – 264 с.
  23. Магнус В., Каррас А., Солитэр Д. Комбинаторная теория групп. Пер. с англ. – М.: Наука. Гл. ред. физ.–мат. лит., 1974. – 455 с.
  24. Макаренков. Алгоритмы на словах // Квант.–1977. –№2. –с.2–9.
  25. Мальцев А.И. Алгебраические системы. – М.: Наука. Гл. ред. физ.–мат. лит., 1970.
  26. Математическая энциклопедия. В 5 т. / Гл. ред. И.М.Виноградов. – М.: Советская Энциклопедия., 1977 – 1985 гг.
  27. Математический цветник / Сост. и ред. Д.А.Кларнер; Пер. с англ. Данилова Ю.А.; Под ред., с предисл. и прилож. И.М.Яглома. – М.: Мир, 1983. – 494 с.
  28. Михайлов О. Одиннадцать правильных паркетов//Квант.–1979.– №2. – с.9
  29. Несколько орнаментов по мотивам Эшера // Квант. – 1991. – №2.– с.7–8.
  30. Окунев Л.Я. Основы современной алгебры. – М.: Уч.педгиз., 1941
  31. Савин А Симметрия // Квант.–1997. – №2. – с.28–31.
  32. Фаддеев Д.К. Лекции по алгебре. – М:. Наука, 1984.
  33. Федоров Е.С. Основные работы по симметрии и структуре кристаллов. – М.: Изд–во АН СССР, 1949.
  34. Фор Р., Кофман А., Дени–Папен М. Современная математика. – М.: Мир, 1966.
  35. Фрид Э. Элементарное введение в абстрактную алгебру. М.: Мир, 1979.
  36. Холл М. Теория групп. – М.: ИЛ, 1967.