Множества и операции над ними
| Вид материала | Документы |
- Тема №1. Множества и операции над ними, 74.19kb.
- Повторение: множества и операции над ними; рациональные выражения (Мерзляк, 4.69kb.
- Программа курсу «Математический анализ», 69.36kb.
- Программа вступительного экзамена в аспирантуру цэми ран по специальности 08. 00., 84.35kb.
- Для кафедр пм и к вопросы по курсу «Дискретная математика». 19. 05. 2010г, 52.29kb.
- Программа курса "Основы дискретной математики", 14.41kb.
- Календарно-тематический план учебная дисциплина: «Математика», 34.71kb.
- Вопросы к экзамену по математическому анализу (зимняя сессия), 53.55kb.
- Программа по математике для поступающих в рамэк, 92.57kb.
- Множества, 45.64kb.
Глава 1 Теория множеств
Тема 1 Множества и операции над ними Занятие 1
- Какой способ использован при задании множеств:
а) IVT = {множество групп факультета ИВТ}; б) P42 = {множество студентов группы П-42}? Верно ли, что: P42 IVT? P42 IVT?
- Перечислить все элементы множества {x | x – целое и x2 < 49}.
- Описать множество {3, 6, 9, 12, 15, 18, 21, 24} при помощи характеристического свойства.
- Перечислить все подмножества множества {a,b,c}.
- Справедливо ли равенство: {{a,b},{b,c}} = {a,b,c}?
- Пусть E = {0, 2, 4, 6,…} – множество всех целых четных чисел; N = {1,2,3,…} – множество натуральных чисел. Определить, из каких чисел будут состоять множества: E N, E N, E \ N, N \ E?
- Доказать, что {}.
- Установить истинность или ложность каждого из следующих утверждений: а) ; б) A, где A – произвольное множество; в) ; г) ; д) A, где A – произвольное множество.
- Определить количество элементов в каждом множестве:
а) {,{}}; б) {{,{}}}; в) {1,2,3,{1,2,3}}; г) {,{},a,b,{a,b},{a,b,{a,b}}}; д) {,{},{,{}}}.
- Доказать, что если множества A B и B C, то A C.
- Пусть даны множества A = {1,2,3,4,5,6,7}, B = {4,5,6,7,8,9,10}, C = {2,4,6,8,10}, U = {1,2,3,4,5,6,7,8,9,10}. Определить множества:
а) A C; б) A B; в) (A B) C; г) A \ B; д) U\(A B); е) A B; ж) A (B C); з) A Δ B; и) (A C) \B; к) B Δ C; л) (A \ ) (A \ A).
- О
 пределить, какие из следующих утверждений верны, а какие – нет:
пределить, какие из следующих утверждений верны, а какие – нет:
а) A = A; б) A Δ A = ; в) если A B, то A B = A; г) A \ A = A; д) A = A; е) если A B = A, то B A; ж) A \ = A; з) A Δ = A; и) если A B, то A B = A;
к) A B =A B; л) A = A; м) если A B = A, то B A.
- Доказать, используя определения операций и , что для любых множеств A, B, C выполняется: а) A(BC) = (AB)(AC); б) (A B) A = A; в) (A B) A = A; г) A \ B = A B.
- Определить операции , , \ через: а) Δ, ; б) Δ, ; в) \, Δ.
- Доказать, что A\(A\B) = AB. Проиллюстрировать графически.
- Доказать, что A\B = A\(AB). Проиллюстрировать графически.
- Пусть множества A, B, C удовлетворяют соотношениям: B A, A C = . Решить систему уравнений:
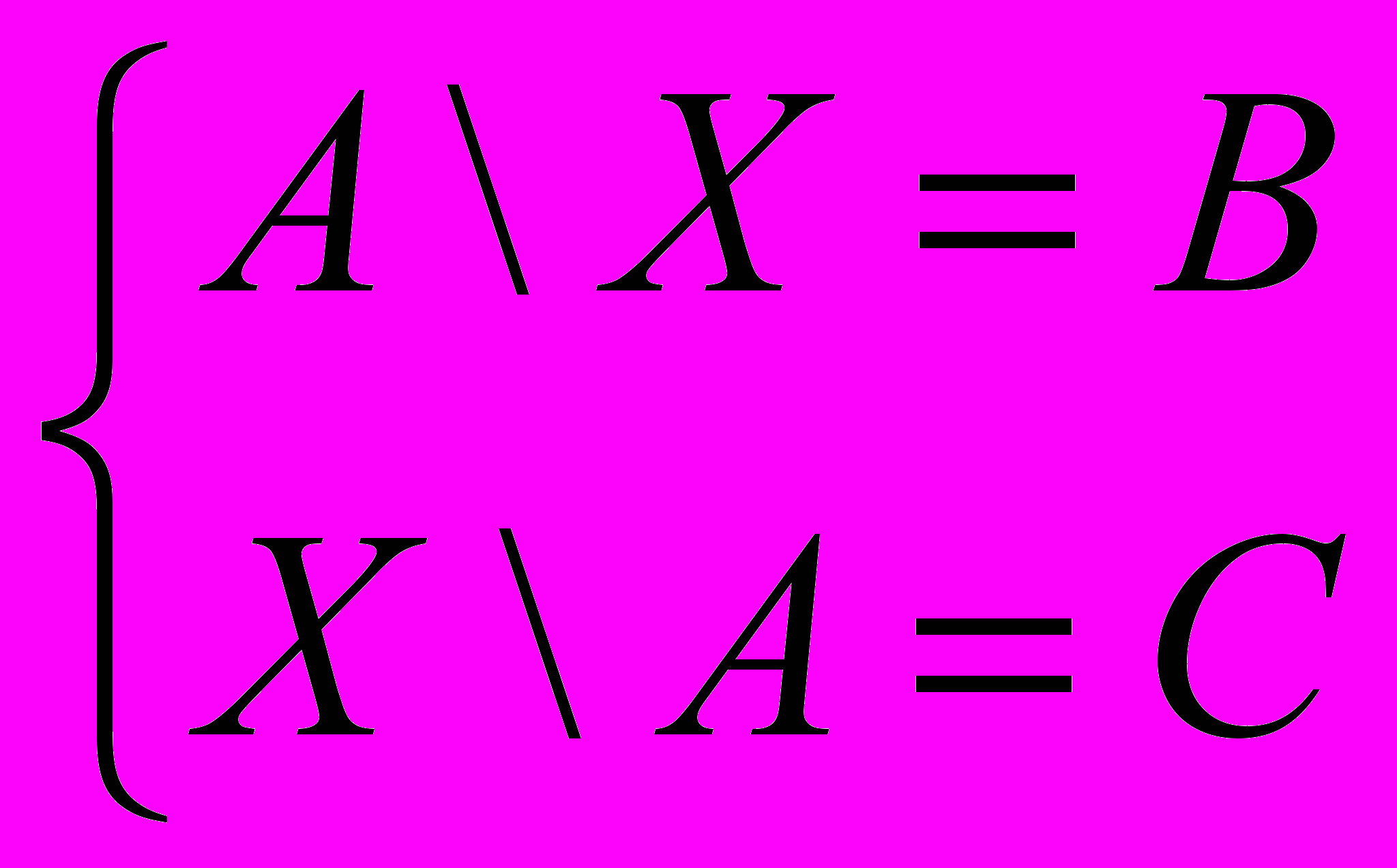
- Пусть множества A, B, C удовлетворяют соотношениям: B A C. Решить систему уравнений:
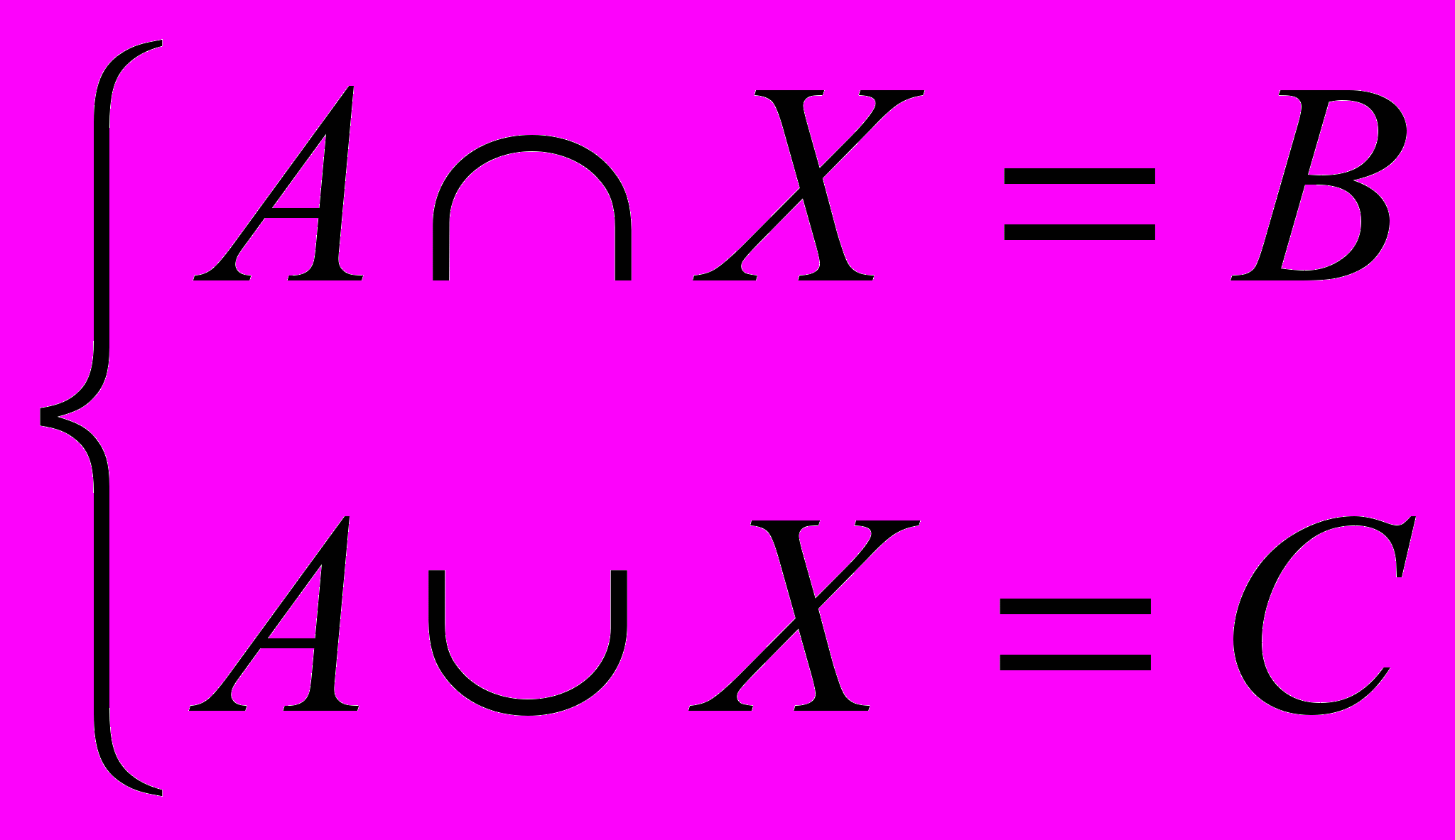 .
.
- Пусть множества A, B, C удовлетворяют соотношениям: B A C. Решить систему уравнений:
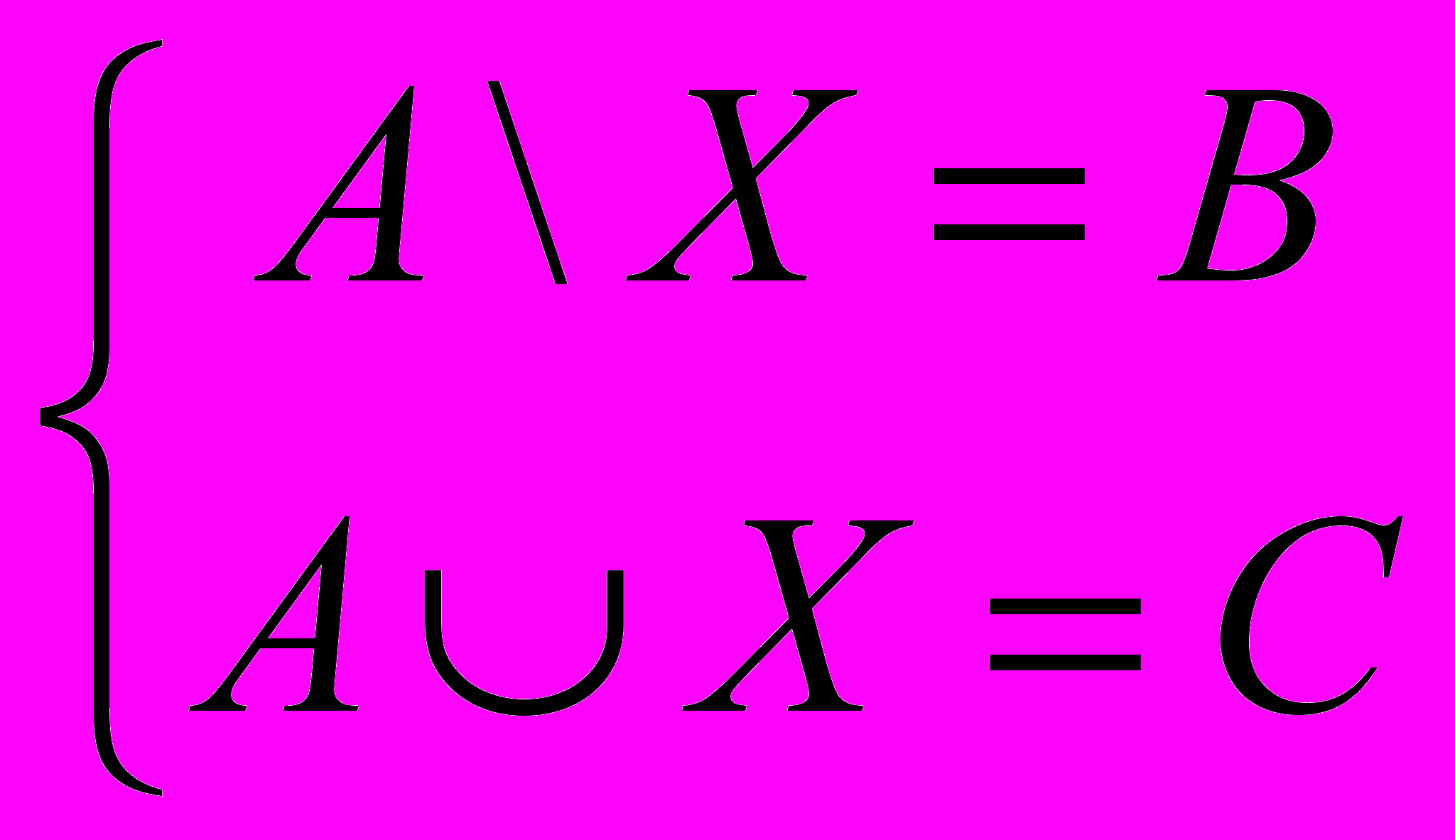 .
.
- Доказать аналитически, используя свойства операций над множествами, и проиллюстрировать графически:
а) A\(A\B)=AB; б) A\B=A\(AB); в) AΔ(AΔB)=B;
г) AΔB=A\B, если BA; д) (AB)\(AB)(A\B)(B\A).
- Указать такие множества A, B, C, что (A\B)\С A \ (B \ С).
- При каком условии на множества A, B, C выполняется
(A\B)\С = A \ (B \ С)?
- Пусть A={a,b,c,d}. Какие из следующих классов множеств составляют разбиение или покрытие множества A? а) {{a,b},{a,c},{c,d}}; б) {{a,d},{c},{d},{b}}; в) {{a},{c,d}}; г) {{a},{b,c,d}}.
- Выписать все варианты непустых разбиений множества A={a,b,c,d}.
Тема 2 Отношения и функции Занятие 2
- Пусть A = {1,2,3}, B = {a,b}. Определить:
а) A B; б) B B; в) A ; г) B A; д) A Δ B.
- Выяснить, справедливы ли равенства. Если нет – привести контрпример.
а) (AB)C = (AB)(BC); б) (AB)C = (AС)(BC);
в) (AB)(CD) = (AB)(CD); г) (AB)(CD) = (AC)(BD); д) (AB)(CD) = (AC)(AD)(BC)(BD).
- Найти область определения и множество значений отношений:
а) {(a,1),(a,2),(c,1),(c,2),(c,4),(d,5)}; б) {(1,2),(2,4),(3,6),(4,8),…};
в) {(x,y) | x,yR и x = y2}; г) {(x,y) | x,yI и x2 + y2 16}.
- Установить, какие из приведенных совокупностей элементов составляют разбиение множества A={1,2,3,4,5,6,7}. Для тех, что составляют, перечислить элементы соответствующего отношения R, такого, что aRb a,b одному Ai: а) {{1,2},,{3,4,5},{6,7}}; б) {{1,2},{3,4,5},{6,7}}; в) {{1,7},{3,4,6}}; г) {{1,5},{3,4,5},{2,6,7}}; д) {{1,2,3,4,5,6,7}}.
- На плоскости задана декартова прямоугольная система координат. Указать точки плоскости, соответствующие элементам отношения R N2, если: а) R = {(x,y) | x 6, y 4, x > y}; б) R = {(x,y) | x 10, y 10, x делит y}.
- Представить заданное бинарное отношение R на множестве А списком пар; построить его графически; выписать область определения и область значений: А={1,2,3,4,5}, R={(x,y)| остаток от деления y на x равен 1}.
- Пусть А={1,2,3,4}, отношения R1,R2 А2: R1={(x,y) | 2x y}, R2={(x,y)| x+3y четно}. Построить R1, R2, R = R2◦R1, выписать области определения и области значений всех трех отношений.
Занятие 3
- Даны множества: A = {1,2,3,4,5}, B = {6,7,8,9}, C = {10,11,12,13}; отношения: R AB, S BC: R ={(1,7),(4,6),(5,6),(2,8)}, S={(6,10),(6,11),(7,10),(8,13)}. Определить: а) R–1 и S–1; б) S◦R; в) R–1◦S–1; г) S◦S–1 и S–1◦S.
- Пусть R – множество всех действительных чисел; N = {1,2,3,…}. Найти:
а) –1; б) ◦; в) –1◦; г) ◦–1, если отношение определено:
1) = {(x,y) | x,y N и x делит y};
2) = {(x,y) | x,y R и x+y 0};
3) = {(x,y) | x,y R и 2x3y };
- Определить, являются ли указанные отношения на множестве N рефлексивными, транзитивными, симметричными, антисимметричными?
а) {(m,n) | m и n взаимно просты}; б) {(m,n) | m делится на n}; в) {(m,n) | m – n =3}; г) {(m,n) | (m + 2n ) кратно 3}.
- Определить на множестве {a,b,c} отношение:
а) эквивалентности; б) частичного порядка;
в) рефлексивное, симметричное, не транзитивное;
г) рефлексивное, транзитивное, не симметричное;
д) симметричное, транзитивное, не рефлексивное.
- Является ли каждое из приведенных ниже отношений R A2 отношением эквивалентности? Если да – построить классы эквивалентности:
а) A=P (M), если M={a,b,c,d}, sRt, если s и t имеют одинаковую мощность;
б) A= Z, R={(a,b), | a+b = 0};
в) A={1,2,3,4,5,6,7,8,9,10}, aRb, если a+b > 0;
г) A={1,2,3,4,5,6,7,8,9,10}, aRb, если a+b четное;
д) A=Z, R={(a,b), если kZ | a–b = 5k};
е) A={множество прямых на плоскости}, nRm, если прямые n и m пересекаются;
ж) A={множество прямых на плоскости}, nRm, если прямые n и m параллельны.
- Пусть C = {1,2,3} и X – булеан множества C с заданным на нем отношением частичного порядка . Определить (если это возможно):
а) точную верхнюю грань для подмножества X {,{1},{2}};
б) подмножество X, для которого точной верхней гранью является {1,3};
в) точную нижнюю грань для X и подмножеств из а) и б).
- Пусть X – множество с заданным на нем отношением частичного порядка . Определить максимальные и минимальные элементы; точные верхнюю и нижнюю грани (если возможно):
а) X = {,{1},{2},{3},{1,2},{1,3},{2,3}}; б) X = {{1},{2},{3},{1,2},{1,3},{2,3},{1,2,3}}.
Занятие 4
- П

 усть f RR. Найти область определения и область значений следующих функций:
усть f RR. Найти область определения и область значений следующих функций:
а) f(x)=x2+4; б) f(x)=(x–2); в) f(x)=1/(x–2); г) f(x)=1/(x2+4).
- Д
 ля функций f и g, заданных на множестве действительных чисел, найти f(g(x)) и g(f(x)), если:
ля функций f и g, заданных на множестве действительных чисел, найти f(g(x)) и g(f(x)), если:
а) f(x) = x2+1; g(x) = x + 3; б) f(x) =x2+2; g(x) = x2 + 3;
в) f(x) = 1 / x; g(x) = 2x + 3.
- Выяснить, какие из следующих функций, у которых область определения и область значений совпадает с действительной числовой осью, являются инъективными, сюръективными, имеют обратную функцию:
а) f(x) = |x|; б) f(x) = x2+4; в) f(x) = x3+6; г) f(x) = x+|x|; д) f(x) = x(x–2)(x+2).
- На множестве {0,1,2,3,4,5} задать функцию:
а) не инъективную; б) биективную.
- На множестве N задать функцию: а) не инъективную; б) инъективную, но не сюръективную; в) сюръективную, но не биективную; г) биективную.
- Используя принцип математической индукции, доказать:
а) неравенство Бернулли: (1+a)n 1 + an n N и a > –1, aR;
б) n Z, n > 0 n3 – n делится на три;
в)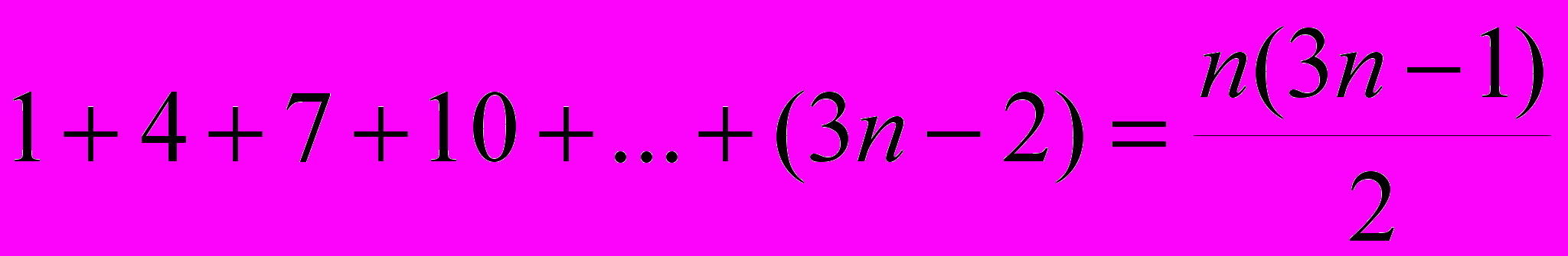 ;
;
г)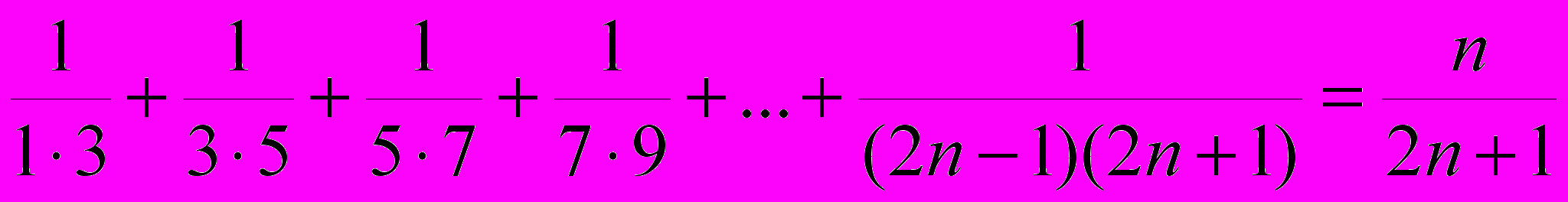 ;
;
д) 1 + 2 + 22 + 23 + … + 2n–1 = 2n–1;
е) 1 + 3 + 5 + 7 + … + (2n – 1) = n 2.
При выполнении лабораторных работ необходимо предусматривать обработку возможных ошибок ввода. Программа не должна «зависать» или вести себя иным некорректным образом ни при каких начальных данных!
Лабораторная работа № 1 Множества и операции над ними
Написать программу, в которой для конечных упорядоченных множеств реализовать все основные операции (, , , \) с помощью алгоритма типа слияния (по материалам лекции 1). Допустима организация множеств в виде списка или в виде массива.
Работа программы должна происходить следующим образом:
1. На вход подаются два упорядоченных множества A и B (вводятся с клавиатуры, элементы множеств – буквы латинского алфавита).
- После ввода множеств выбирается требуемая операция (посредством текстового меню, вводом определенного символа в ответ на запрос – выбор по желанию автора). Операции: вхождение AB, AB, AB (дополнительно: A\B, B\A, AB).
- Программа посредством алгоритма типа слияния определяет результат выбранной операции и выдает его на экран с необходимыми пояснениями.
- Возврат на п.2 (выбор операции).
- Завершение работы программы – из п.2 (например, по ESC).
Дополнительно: возможность возврата (по выбору пользователя) на п.2 или п.1. Выход в таком случае должен быть предусмотрен из любого пункта (1 или 2).
Лабораторная работа № 2 Отношения и их свойства
Бинарное отношение RA2 (A – конечное множество) задано списком упорядоченных пар вида (a,b), где a,bA. Программа должна определять свойства данного отношения: рефлексивность, симметричность, антисимметричность, транзитивность (по материалам лекции 3).
Работа программы должна происходить следующим образом:
1. На вход подается: а) множество A из n элементов; б) список упорядоченных пар, задающий отношение R (ввод с клавиатуры).
2. Результаты выводятся на экран (с необходимыми пояснениями) в следующем виде:
а) матрица бинарного отношения размера nn;
б) список свойств данного отношения.
Дополнительно: после вывода результатов предусмотреть возможность изменения списка пар, определяющих отношение. Например, вывести на экран список пар (с номерами) и по команде пользователя изменить что-либо в этом списке (удалить какую-то пару, добавить новую, изменить имеющуюся), после чего повторить вычисления.
