Программа для подготовки к зачету теоретическая часть
| Вид материала | Программа для подготовки |
- Программа для подготовки к зачету I. Теоретическая часть, 68.7kb.
- Программа для подготовки к зачету (экзамену) теоретическая часть, 113.03kb.
- Программа для подготовки к зачету теоретическая часть, 54.03kb.
- Программа для подготовки к экзамену теоретическая часть, 101.03kb.
- Программа для подготовки к экзамену теоретическая часть, 254.95kb.
- Рабочая программа по дисциплине «теоретическая фонетика» методические рекомендации, 327.76kb.
- Содержание введение теоретическая часть, 38.74kb.
- Содержание введение теоретическая часть, 38.73kb.
- Программа для подготовки к сдаче вступительного экзамена в аспирантуру по специальности, 174.75kb.
- Л. И. Горбунова, Г. С. Келлер культурология часть I человек – общество культура, 2386.47kb.
МОСКОВСКАЯ ФИНАНСОВО-ЮРИДИЧЕСКАЯ АКАДЕМИЯ
| Согласовано на 2008-2009 уч.год Начальник УМУ__________________С.В. Щедроткина «_____»_______________2009 г. | |
Дисциплина: Дискретная математика
Специальность (направление): Защита информации
Форма обучения: все
Программа для подготовки к зачету
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Список тем
- Понятие множества. Пустое множество. Наиболее употребляемые множества.
- Множества и отношения. Подмножество.
- Операции над множествами.
- Алгебра множеств.
- Сравнение множеств.
- Упорядоченные множества.
- Свойства и отношения.
- Отображения.
- Решетки.
- Основные правила комбинаторики.
- Перестановки, сочетания, размещения, размещения с повторениями.
- Биноминальные коэффициенты.
- Алгебра Буля.
- Формулы алгебры логики.
- Функции алгебры логики.
- Нормальные формы булевой функции (КНФ, ДНФ).
- СДНФ. СКНФ.
- Двойственность алгебры логики.
- Многочлен Жегалкина, классы Поста, теорема Поста.
- Полнота логических связок.
- Электронные логические элементы.
- Язык логики высказываний.
- Понятие семантики в логике высказываний.
- Операции логики высказываний.
- Нормальные формы логики высказываний (КНФ, ДНФ).
- Таблица истинности для формулы.
- Метод резолюции.
- Теоретико-множественная форма представления предложения.
- Понятие предиката.
- Кванторы.
- Язык логики предикатов.
- Подстановка. Композиция.
- Интерпретация и истинность в логике предикатов.
- Унификация в логике предикатов.
- Тавтология, выполнимость и противоречие в логике высказываний и предикатов.
- Предварённая нормальная форма.
- Сколемовская нормальная форма.
- Метод резолюции в логике предикатов..
- Графы. Основные понятия и определения.
- Изоморфизм графов.
- Маршруты, цепи и циклы.
- Матричное задание графов.
- Связность. Компоненты связности.
- Степень вершин графа, орграфа.
- Поиск маршрута в графе.
- Поиск путей (маршрутов) с минимальным числом дуг (рёбер).
- Минимальные пути (маршруты) в нагруженных орграфах (графах).
- Эйлеровы графы.
- Гамильтоновы графы.
- Деревья.
- Остовное дерево графа.
- Понятие алгоритма;
- Определение машины Тьюринга;
- Применение машины Тьюринга к словам;
- Правильная вычислимость функций на машине Тьюринга;
- Тезис Тьюринга;
- Основные понятия теории рекурсивных функций;
- Примитивно рекурсивные функции;
- Тезис Чёрча;
- Марковские подстановки;
- Нормальные алгоритмы и их применение к словам;
- Нормально вычислимые функции и принцип нормализации Маркова;
- Разрешимость и перечислимость множеств;
- Неразрешимые алгоритмические проблемы.
- Теория порождающих грамматик;
- Иерархия Хомского для порождающих грамматик;
- Конечные автоматы;
- Стековые автоматы;
- Машины Тьюринга;
- Линейно ограниченные автоматы.
Вопросы, составленные на указанные темы, могут использоваться для оценки знаний студентов на семинарских занятиях, для промежуточной аттестации, а также для самопроверки при самостоятельном изучении курса.
ПРАКТИЧЕСКАЯ ЧАСТЬ
Типовые задачи.
Множества.
- Доказать тождества.
а) (АВ)(А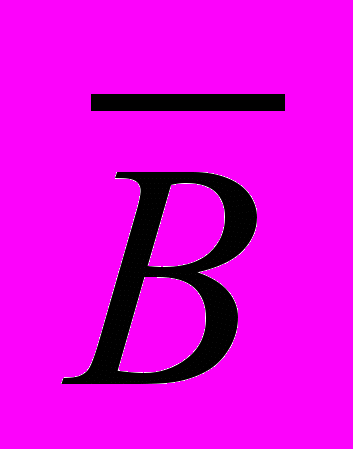 )=А; б) А\В=А
)=А; б) А\В=А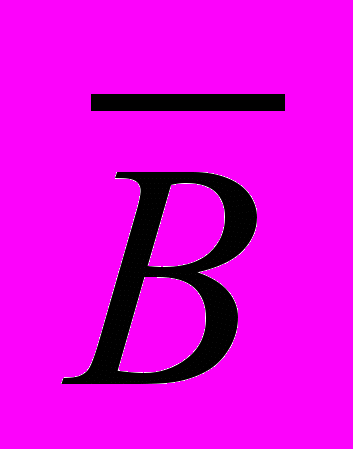
2. Найдите множество Х, удовлетворяющее следующему равенству
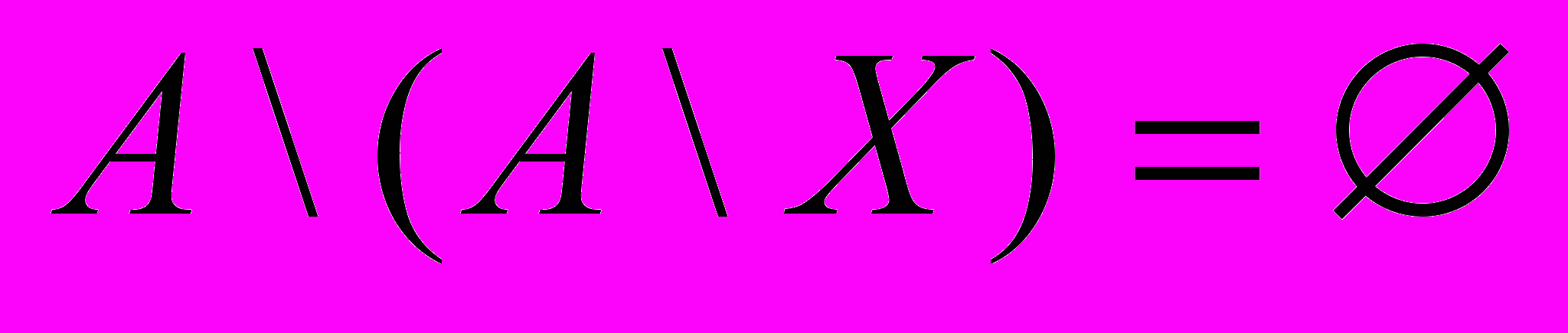 .
.3. Доказать тождество.
(АВ)(А
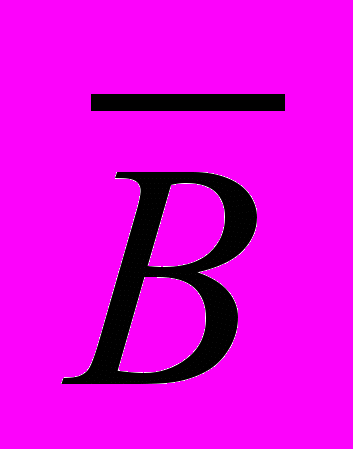 )=А
)=А- Верно ли, что
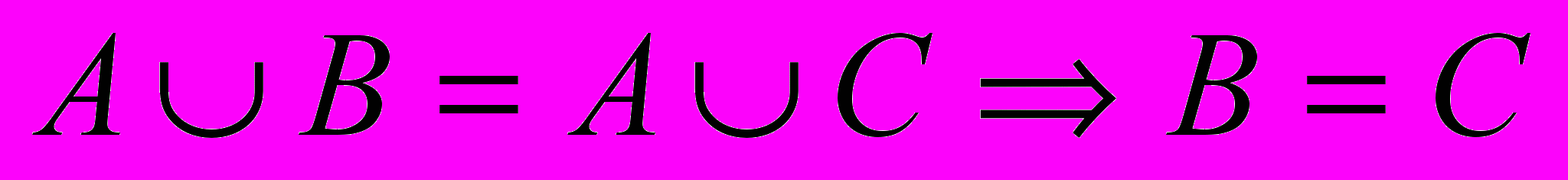 .
.
- Доказать тождество.
(
 В)А=АВ
В)А=АВ- Верно ли, что
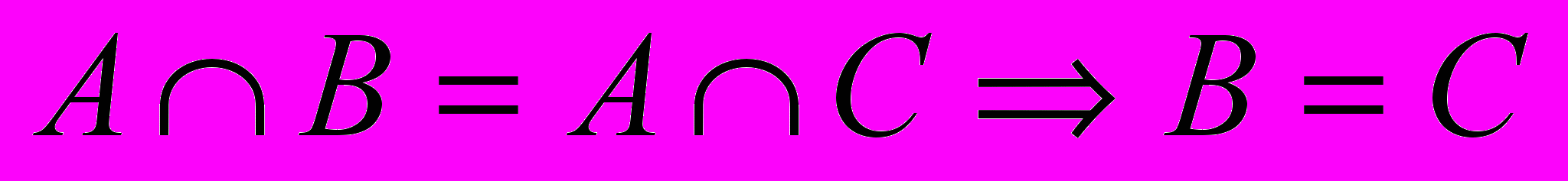 .
.
- Доказать Тождество.
(А\В)\С=(А\С)\(В\С)
- Верно ли, что если
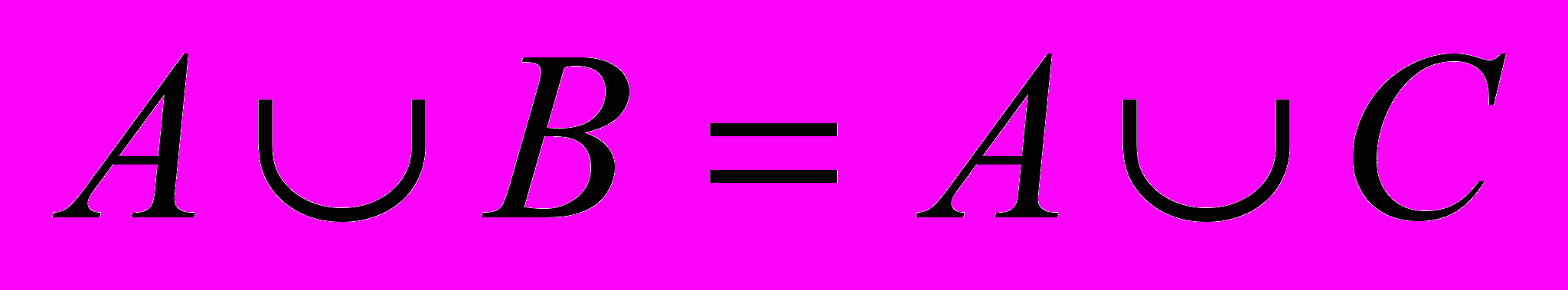 и
и 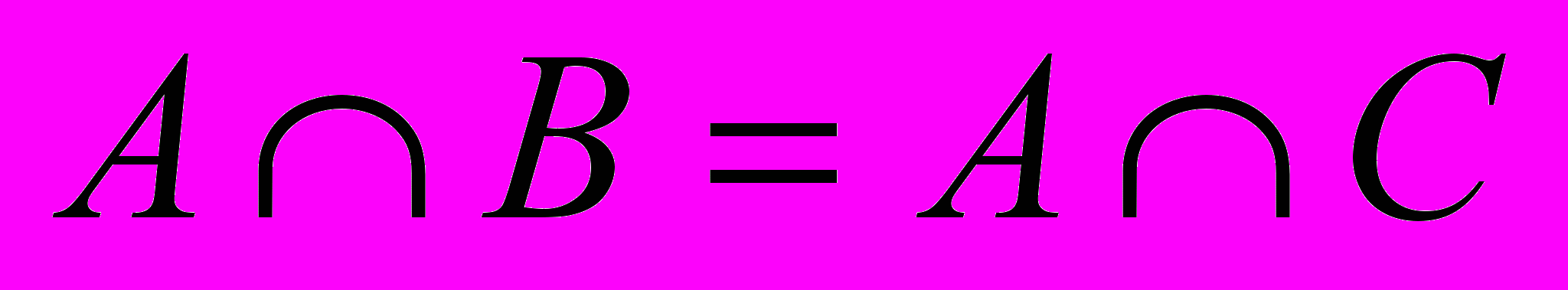 , то, В = С.
, то, В = С.
- Докажите
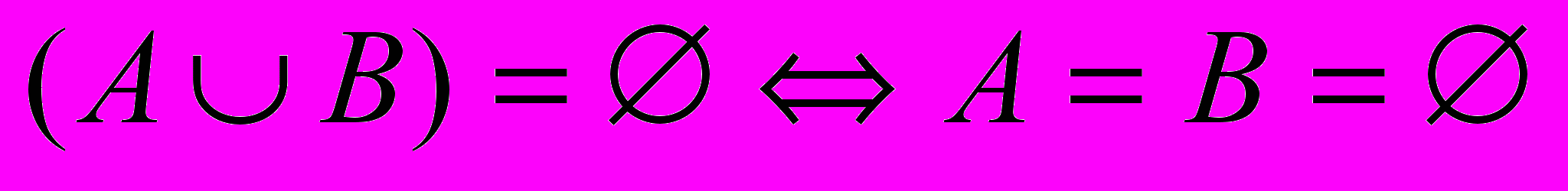 (символ
(символ  означает «тогда и только тогда, когда»).
означает «тогда и только тогда, когда»).
- Докажите
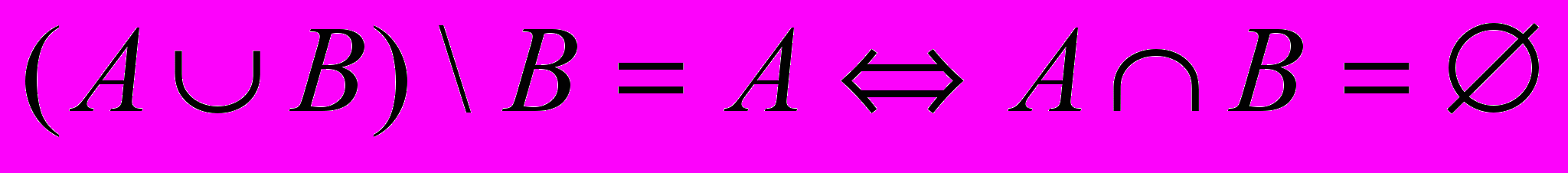 (символ
(символ  означает «тогда и только тогда, когда»).
означает «тогда и только тогда, когда»).
- Доказать тождество.
А(В\С)=(АВ)(А
 )
)- Докажите
 (символ
(символ  означает «тогда и только тогда, когда»).
означает «тогда и только тогда, когда»).
- Доказать тождество.
(А\В)(
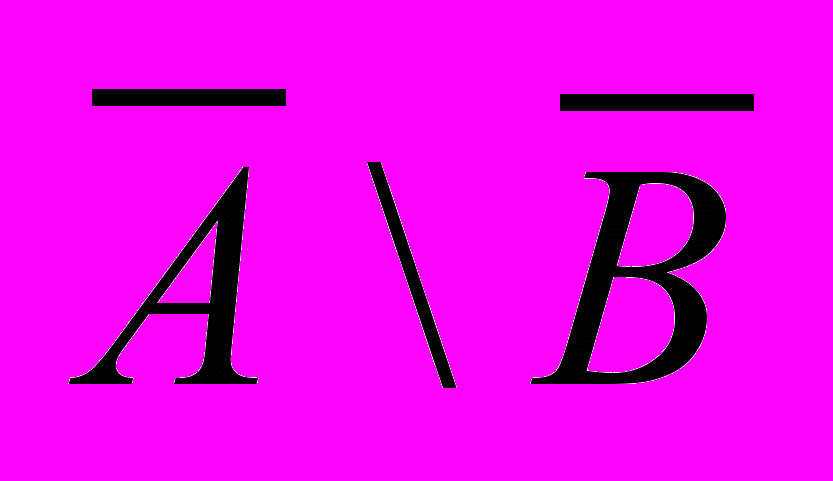 )=(АВ)\(АВ)
)=(АВ)\(АВ)- Докажите
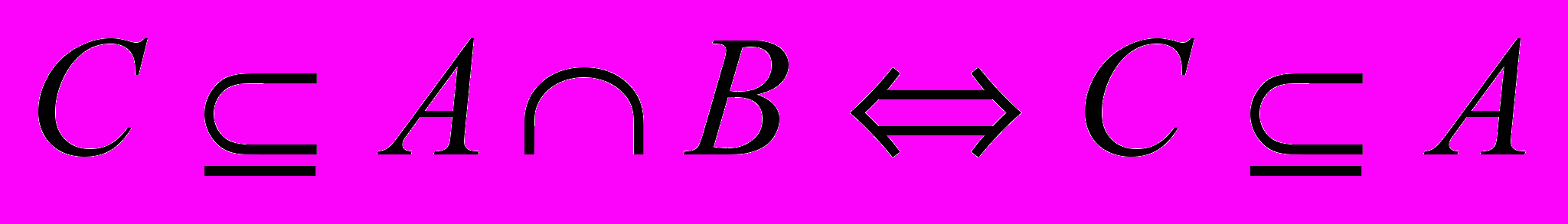 и
и 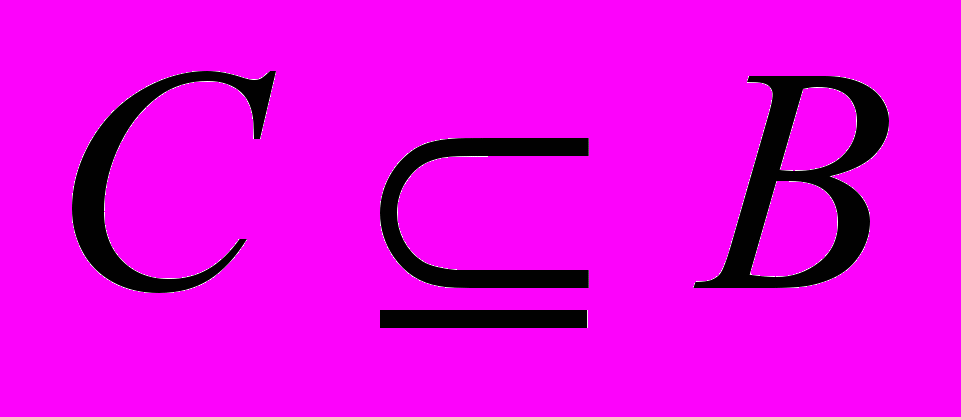 (символ
(символ  означает «тогда и только тогда, когда»).
означает «тогда и только тогда, когда»).
- Доказать тождество.
(
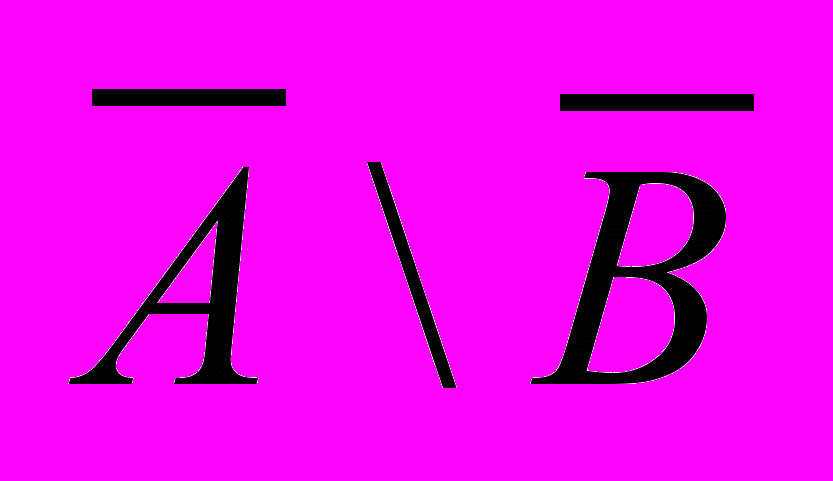 )(
)(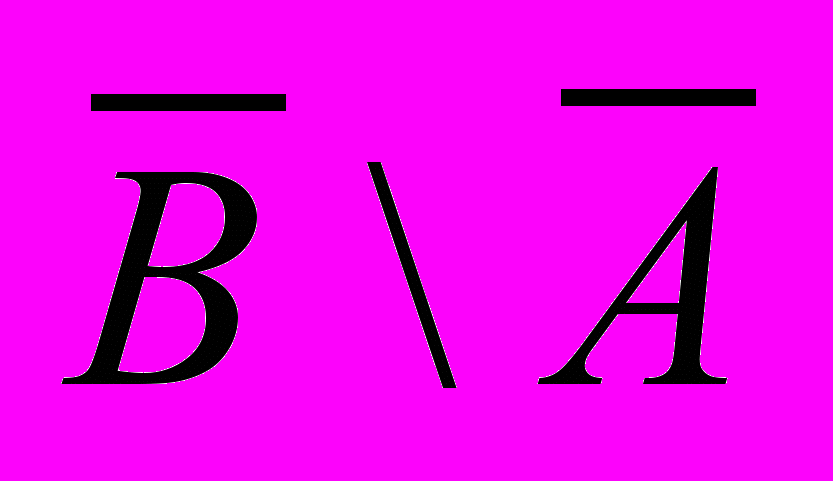 )=(АВ)\(АВ)
)=(АВ)\(АВ)Комбинаторика.
1. Сколько существует способов разместить 3 человека на скамейке?
2. Сколько существует способов расставить 8 книг на полке так, чтобы 3 данные книги стояли вместе?
3. Сколькими различными способами можно выбрать три лица на три различных должности из 8 кандидатов?
4. Сколькими способами можно выбрать 3 лица на 3 одинаковые должности из 8 кандидатов?
5. Сколько различных 6-ти значных чисел можно записать с помощью цифр 1;1;2;2;2;3?
6. Cколько различных перестановок букв можно сделать в словах: замок, ротор, топор, колокол?
7. Сколько прямых можно провести через 8 точек, никакие 3 из которых не лежат на одной прямой, так чтобы каждая прямая проходила через 2 точки?
- Сколько различных шестизначных чисел, начинающихся цифрой 2 и оканчивающихся цифрой 5, можно составить из цифр 1, 2, 3, 4, 5, 6 при условии, что каждая цифра в обозначении числа встречается 1 раз?
9. Найти m и n, если
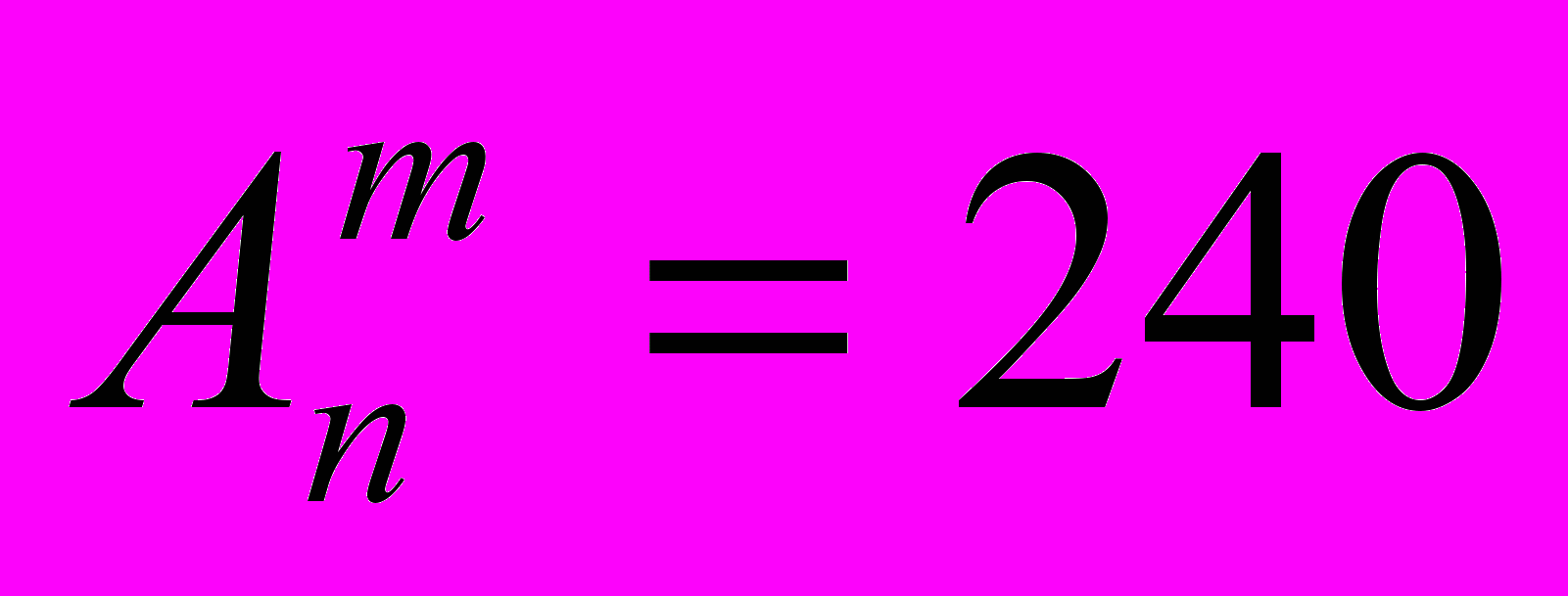 .
.10. Вычислить:
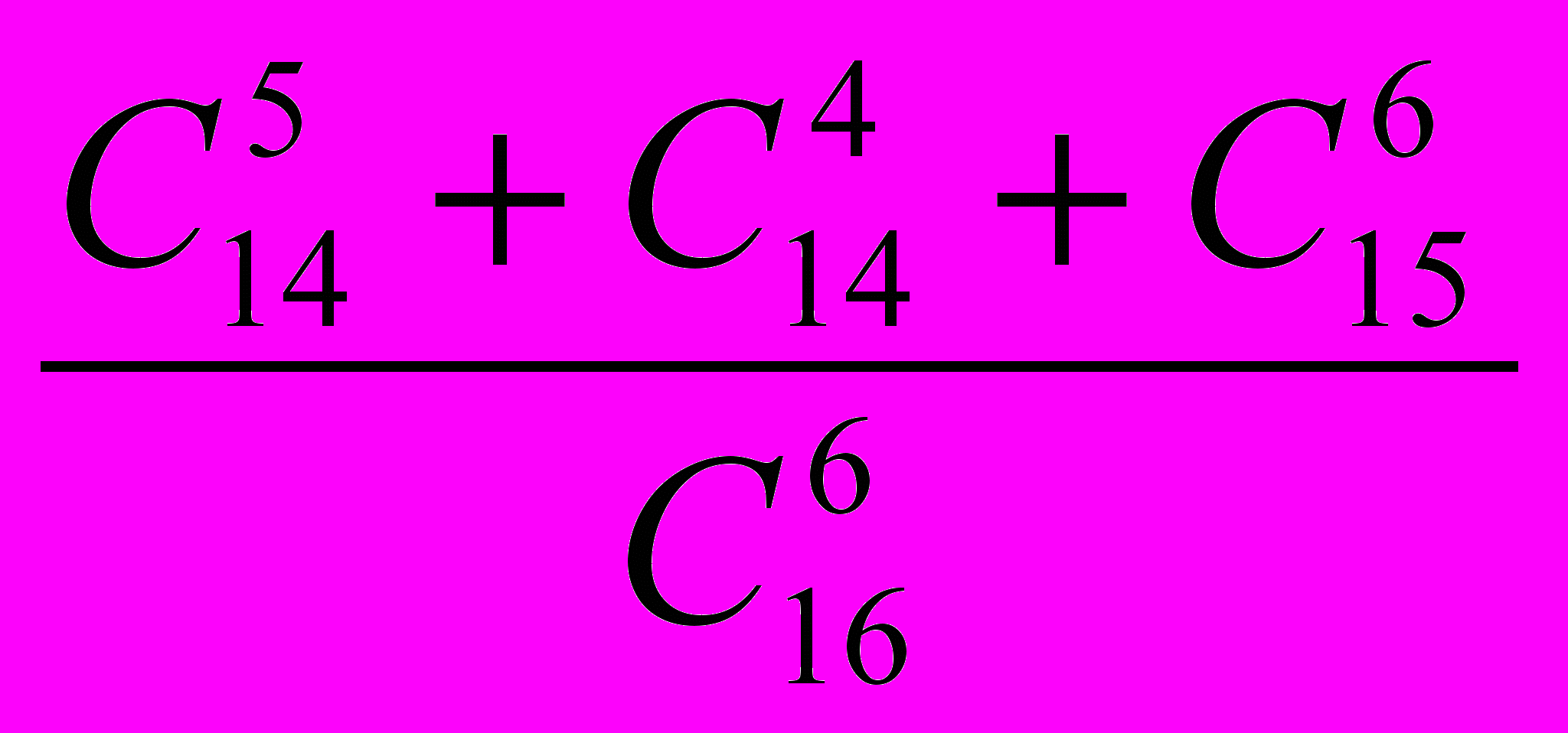 .
. 11. Сколько существует кодовых комбинаций в замке, имеющем 5 дисков и на каждом диске 6 цифр.
Булевы функции.
1. Привести к СДНФ с помощью таблицы истинности и равносильных преобразований. Записать в виде многочлена Жегалкина и построить логическую схему в базисе “И-НЕ”.

2. Доказать, что формула тождественно равна 0 или 1.
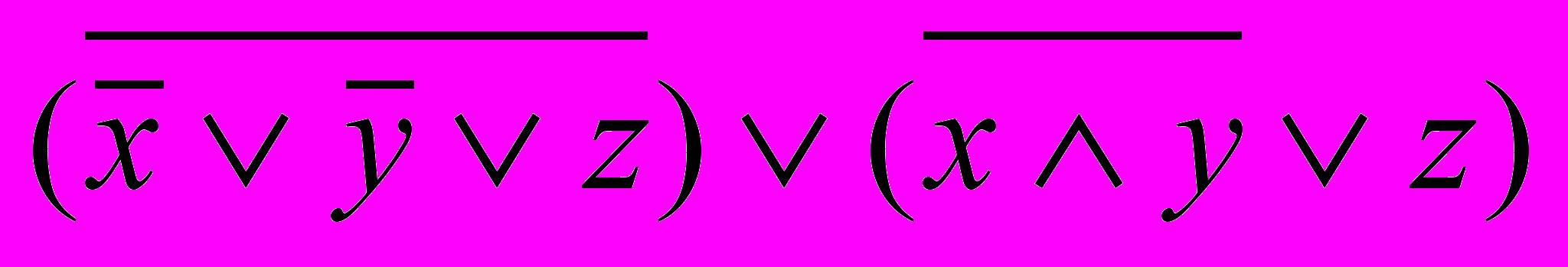
3. Привести к СДНФ с помощью таблицы истинности и равносильных преобразований.
Записать в виде многочлена Жегалкина и построить логическую схему в базисе “И-НЕ”.
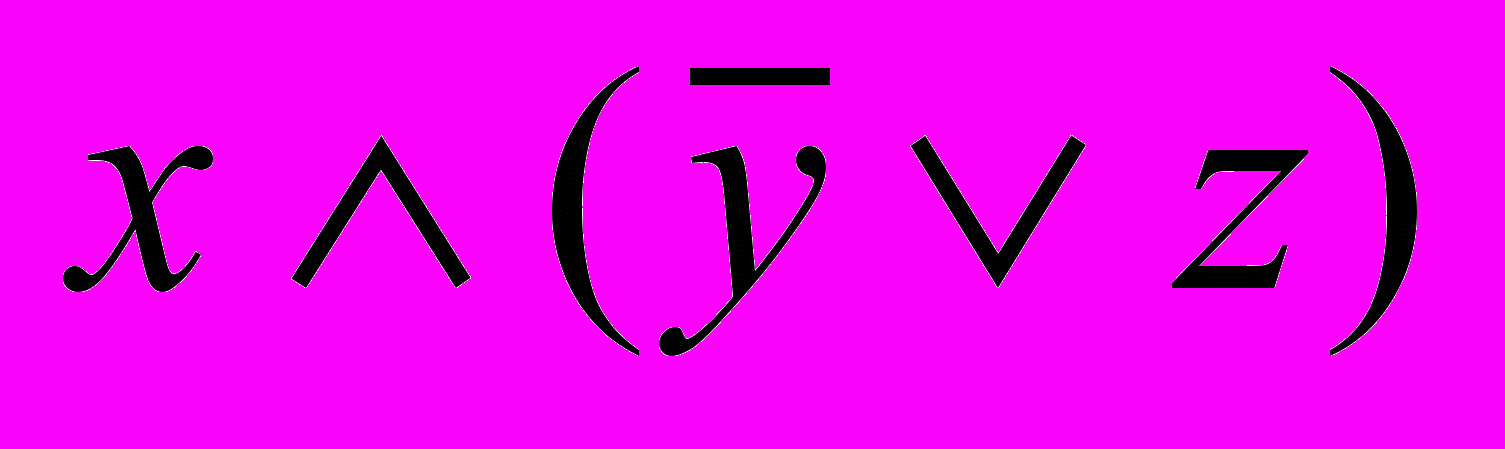
4. Доказать, что формула тождественно равна 0 или 1.
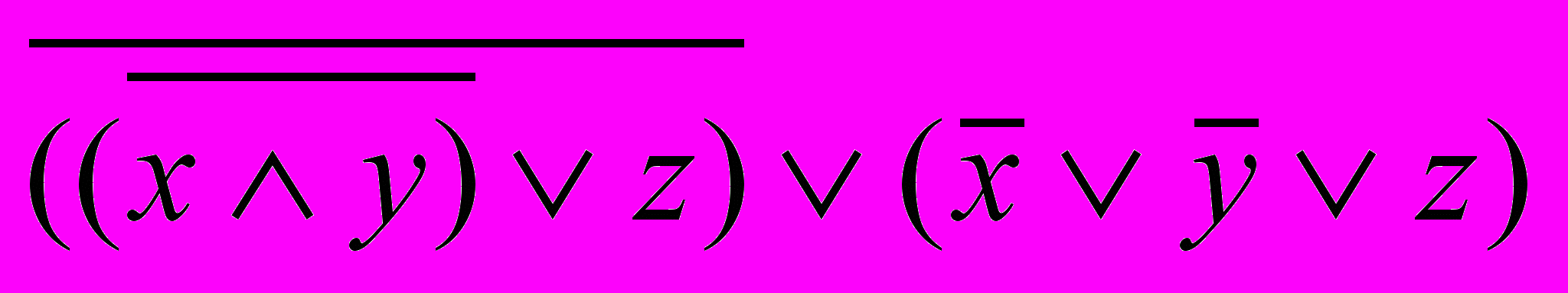
5. Привести к СКНФ с помощью таблицы истинности и равносильных преобразований. Записать в виде многочлена Жегалкина и построить логическую схему в базисе “И-НЕ”.
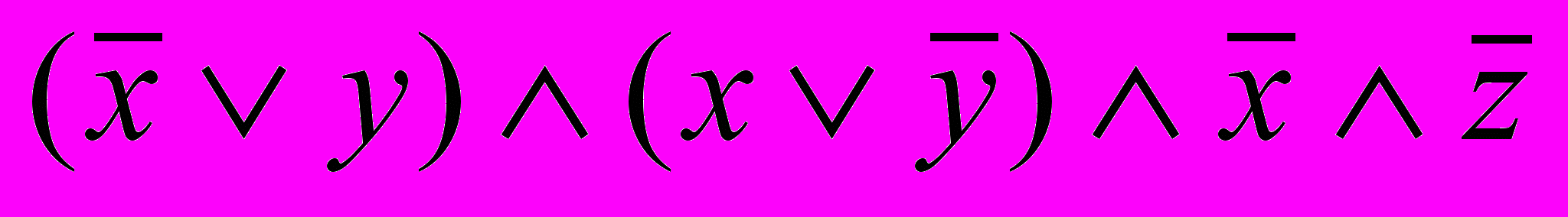
6. Упростить формулу.
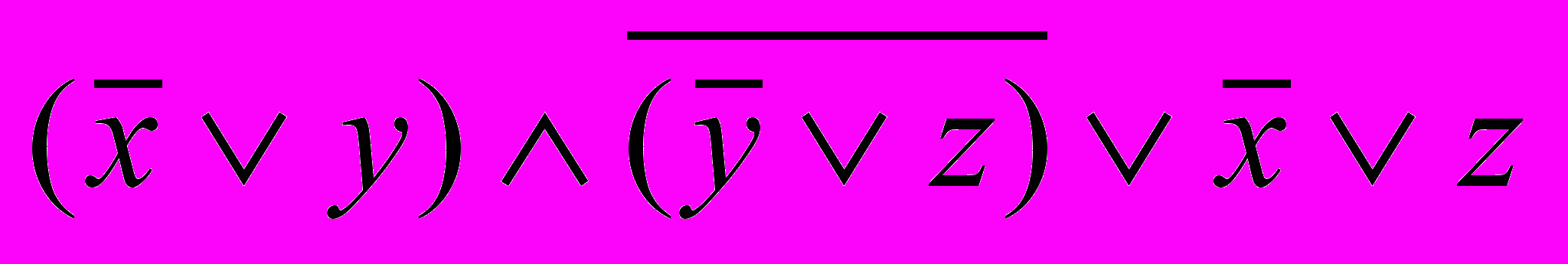
7. Привести к СКНФ с помощью таблицы истинности и равносильных преобразований. Записать в виде многочлена Жегалкина и построить логическую схему в базисе “И-НЕ”.
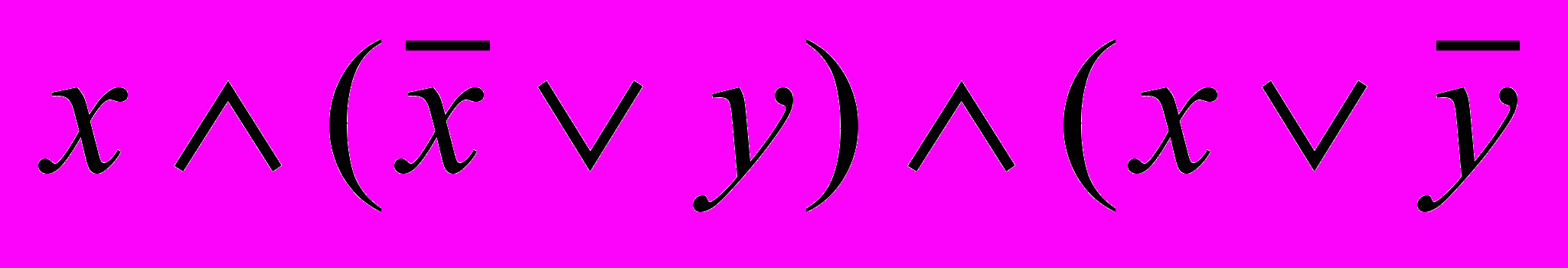
8. Упростить формулу.
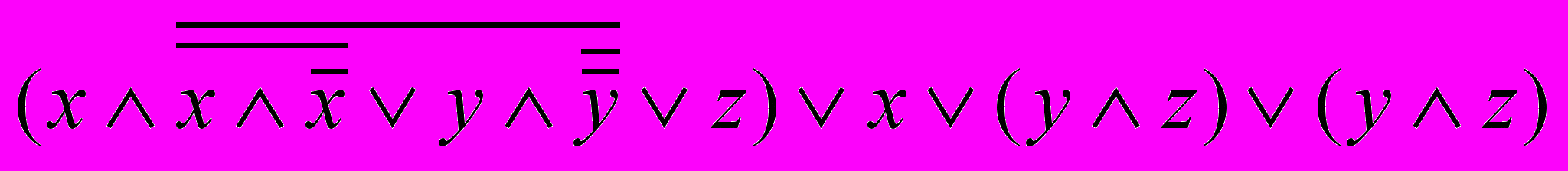

9. Привести к СКНФ с помощью таблицы истинности и равносильных преобразований. Записать в виде многочлена Жегалкина и построить логическую схему в базисе “ИЛИ-НЕ”.
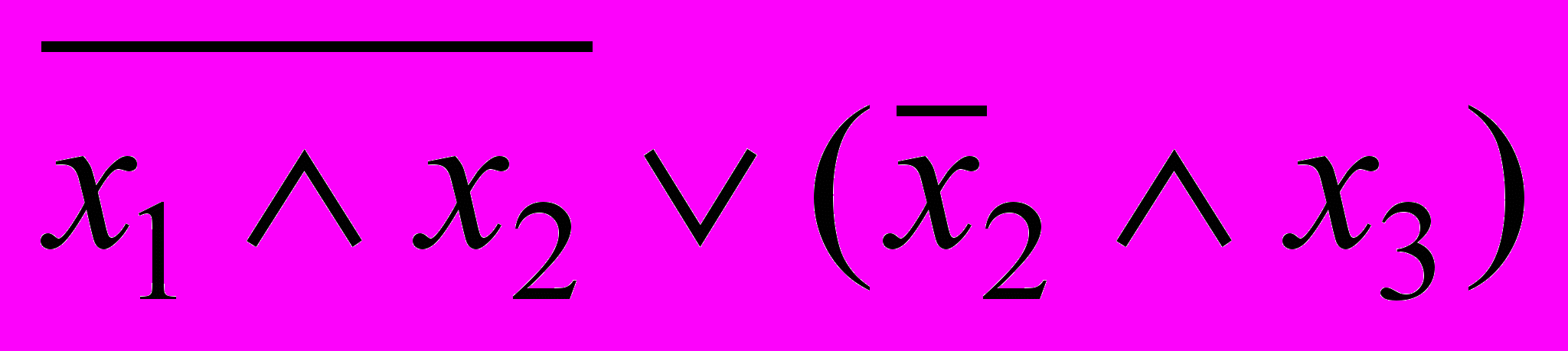
10. Доказать равносильность.

11. Привести к СДНФ с помощью таблицы истинности и равносильных преобразований. Записать в виде многочлена Жегалкина и построить логическую схему в базисе “ИЛИ-НЕ”.

12. Доказать равносильность.
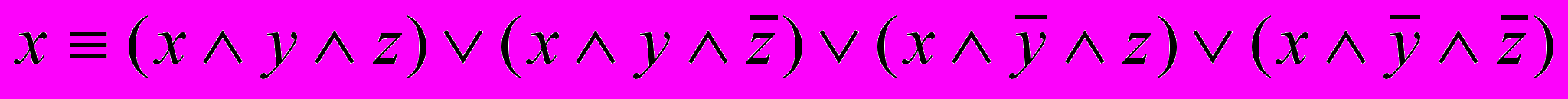

13. Известно, что х=1. Что можно сказать о значении:
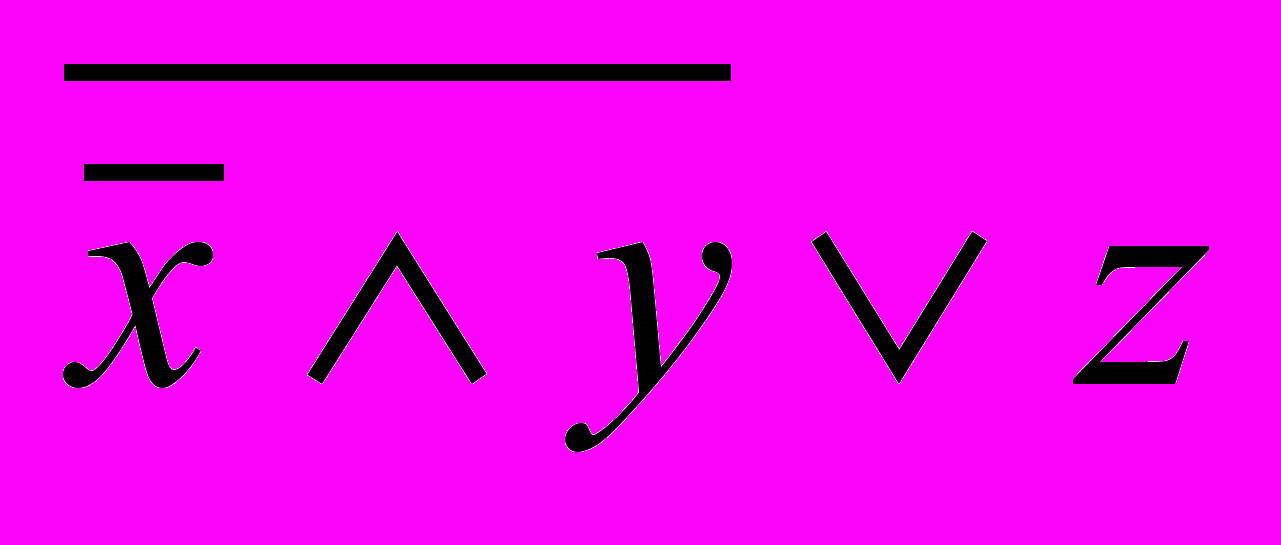 и
и 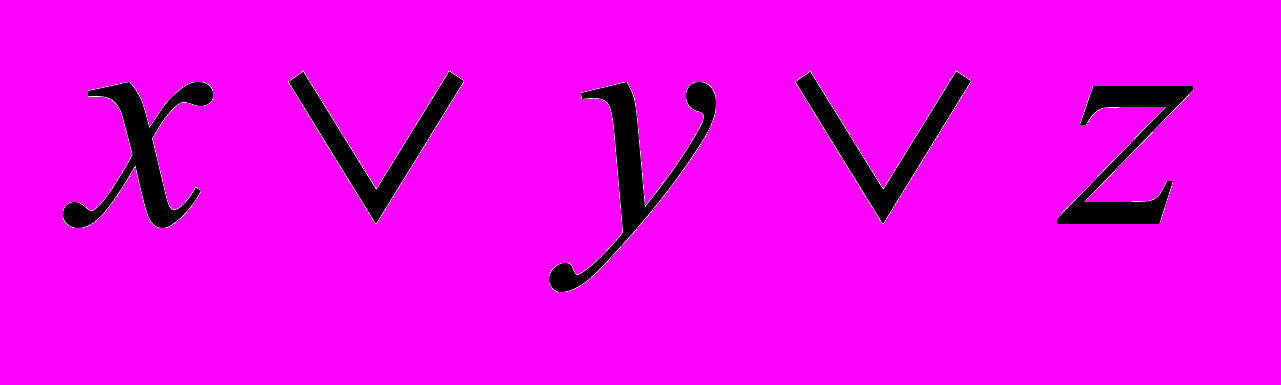 .
.14. Известно, что
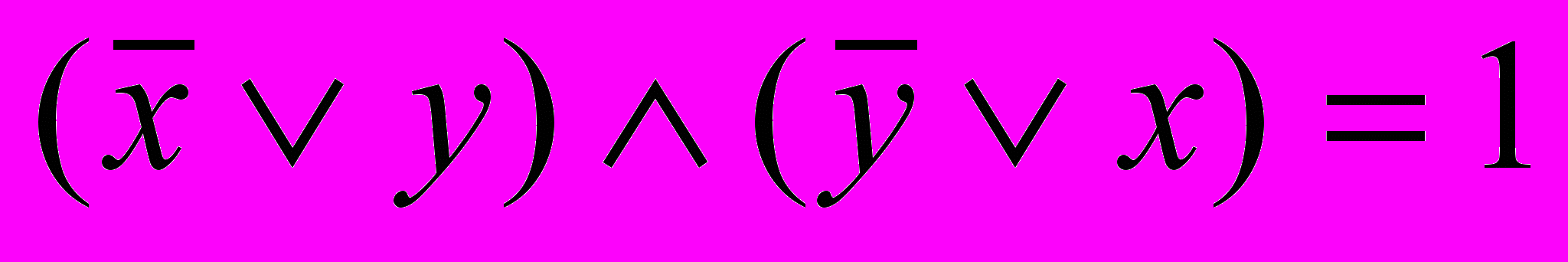 . Что можно сказать о значении:
. Что можно сказать о значении: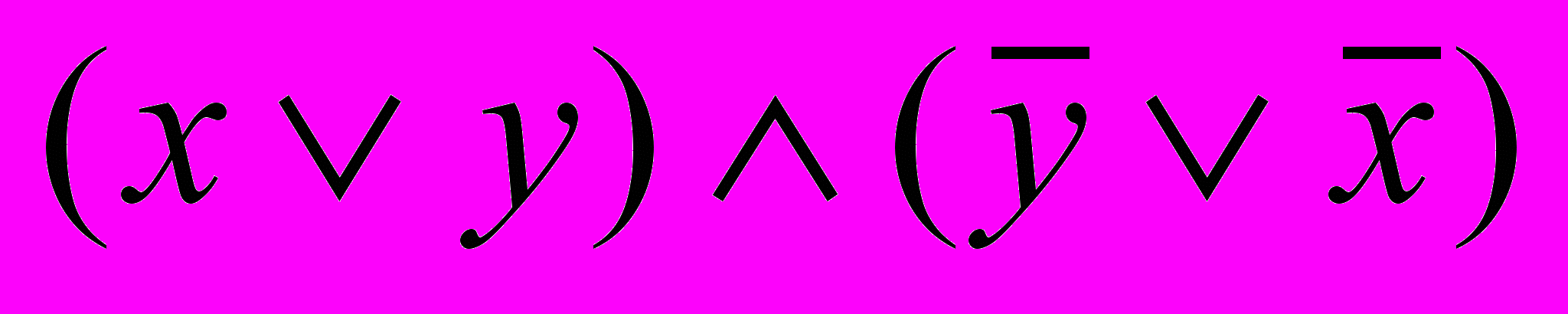 .
.15. Известно, что
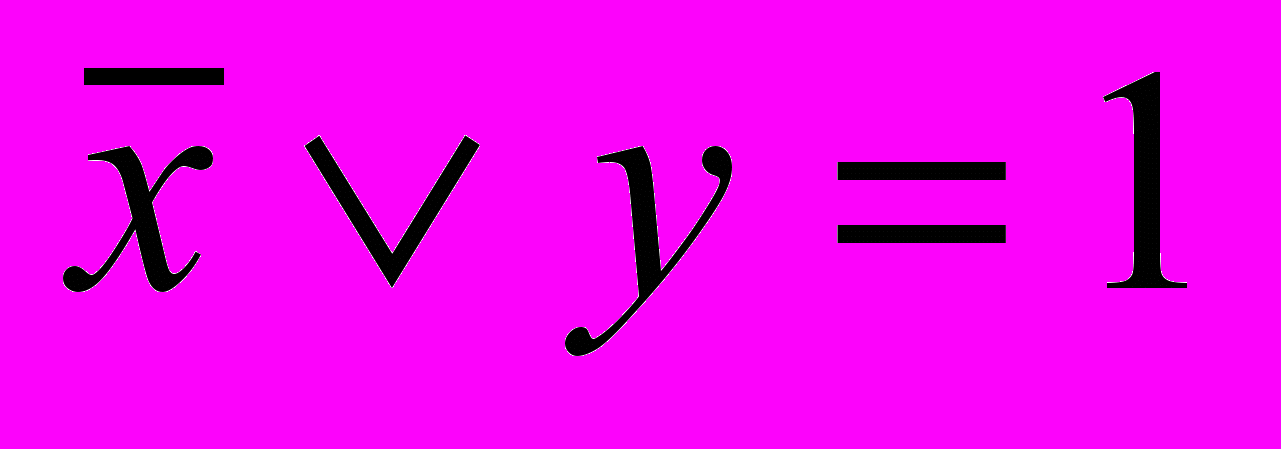 , а
, а 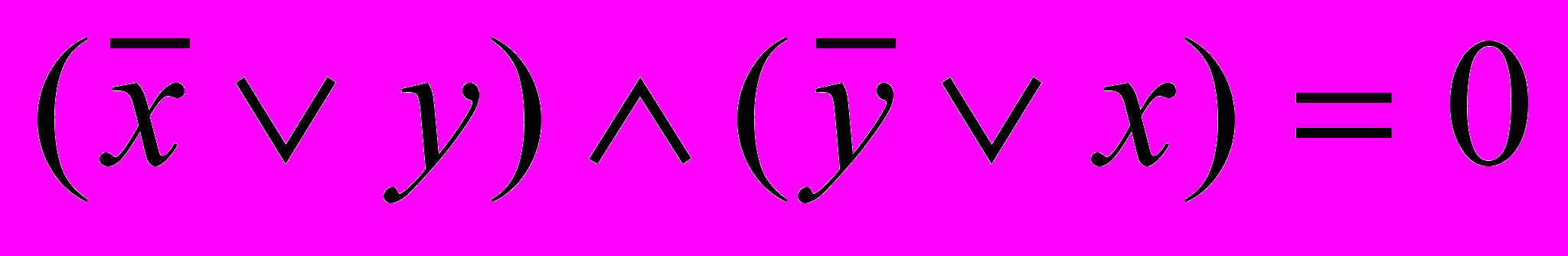 . Что можно сказать о значении:
. Что можно сказать о значении: Логика высказываний.
1.Доказать, что высказывание логически ложно.
а. АВ)(ВС)(АС);
б. ((АВ)(АВ)А;
в. А(ВВ))А.
2. Доказать, что высказывание логически истинно.
а. (АВ)(АВ).
б. (А(АВ))В.
в. (АВ)АВ
3. Докажите, что высказывание является тавтологией.
а. (А→В)(АВ)
б. АВВА.
в. (АВ)(ВА).
4. Найти означивания при которых формула истинна.
а. А(АВ).
б. (АВ)(ВА).
в. (АВ)(АВ).
5. Методом резолюции доказать, что множество S противоречиво.
а. S={ABD, BDA, DA, AB, BD, AB}.
б. S={AB, BC, CA, AC, AC}.
в. S={ABC, ABC, AB, AC, AC}.
6. Методом резолюции доказать, что
а. {AB, CD, DB, BCD}├ BC.
б. {ABC, AB} ├ AC.
7. Представьте следующее высказывание как множество дизъюнктов.
а. А(ВС).
б. ((АВ)С).
8. Определить выполнимо ли множество. Если да, то найти означивания подтверждающие его выполнимость.
а. {{A,B}, {A,B}}.
б. {{A}, {A,B}, {B}}.
9. Определить множество резольвент дизъюнктов S.
а. S={{A,B}, {A,B}, {A}}
б. S={{A}, {B},{A,B}}
в. S={{A}, {B},{A,B}}
Логика предикатов.
1. Выявить логическую форму предложения и записать её на языке логики предикатов.
а. “Каждый студент знает хотя бы некоторых преподавателей”.
б. “Неверно, что никто не знает русского языка.”
в. “Все любят Джейн, но она не любит ни кого.”
г. “Ничто не вечно”.
д. “Разность любых двух положительных чисел меньше суммы этих чисел”.
е. Если он мой отец , то он старше и мудрее меня.”
2. Запишите следующие высказывания на языке логики предикатов:
а. х – мать у, если х – женщина и родитель у.
б. х – отец у, если х – мужчина и родитель у.
в. х – человек, если его родитель человек.
г. х – человек, если отец х – человек.
д. Никто не родитель самому себе.
3. Привести к ПНФ и далее записать предложения в СНФ
а. (х)Р(х)(х)Q(х).
б. (х)(у)[(z)P(x,y)Р(x,z)](u)Q(x,y,u).
в. (x)(y)[(z)P(x,y,z)[(u)Q(x,u)(u)Q(y,u)]].
4. Записать предложение в теоретико-множественной форме.
а. (x)(y)(z)[(P(x,y)Q(x)R(z))(P(x,y)Q(x))(P(x,y)R(z))].
б. (х)(y)[P(x,y)Q(y)].
в. [(x)P(x)(y)(z)Q(y,z)].
5. Если множество дизъюнктов S предложения унифицируемо, то найти НОУ
а. S={{P(a, x, h(g(z)))}, P(z, h(y), h(y))}}.
б. S ={{любит(w,(у))}, {любит(Джон, футбол)}}.
в. S={{Q((w), a, z)}, Q(w, b, (z))}.
г. S={{R(w,y), Q(w, (z),z), R(w,w)}, {R(w,z), Q((w),w,z)}}.
д. S={{P((x),a)},{P(y,(w))}}.
Графы.
- Найти минимальный путь из v1 в v6 методом «фронта волны».
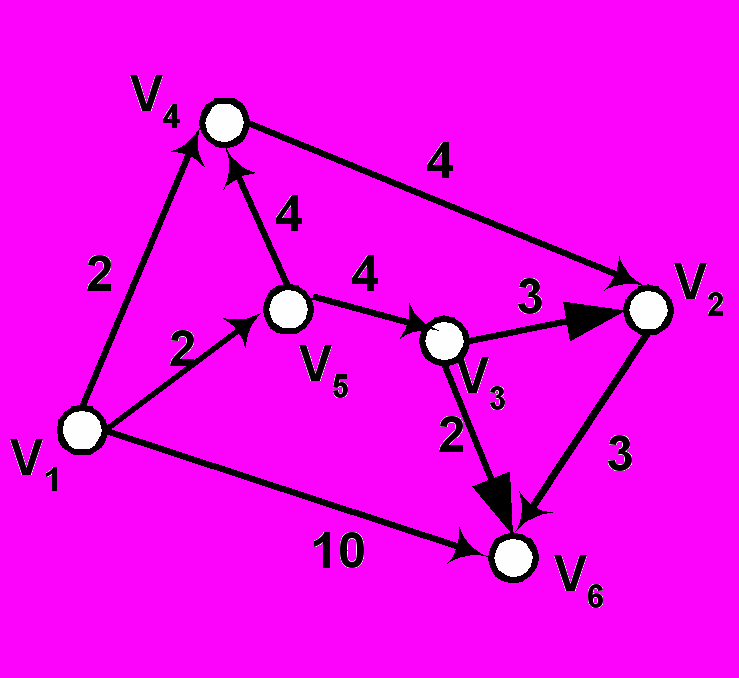
- Найти минимальный путь из v1 в v7 в орграфе, заданном матрицей смежности методом «фронта волны».
А(D) =

- Определить минимальный путь из v1 в v7 в нагруженном орграфе D с числом дуг не более 5.
С(D) =
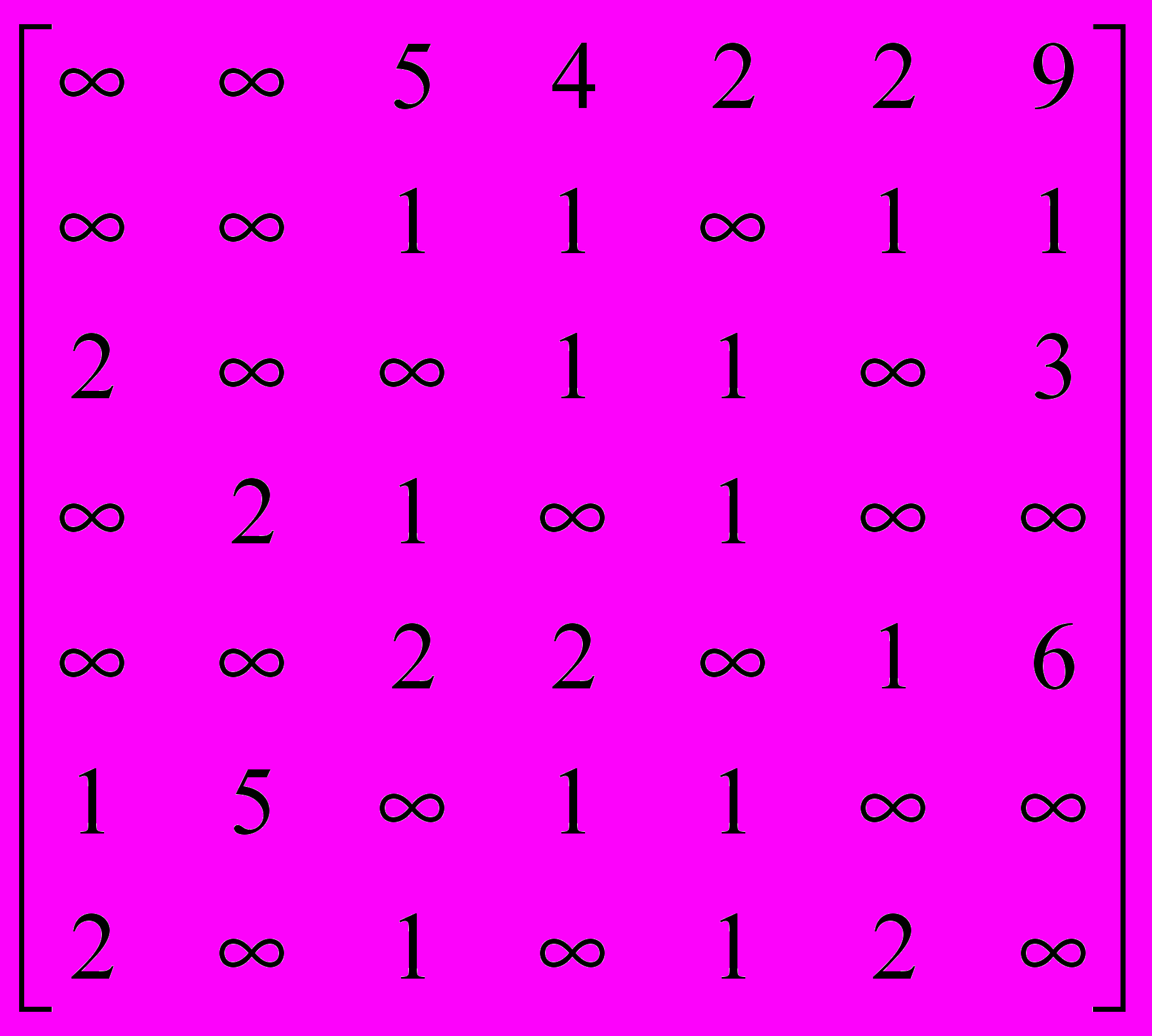
- Проверить существуют ли в мультиграфе, заданном матрицей смежности, эйлеровы цепи и циклы, если да то найти их.
A(G) =
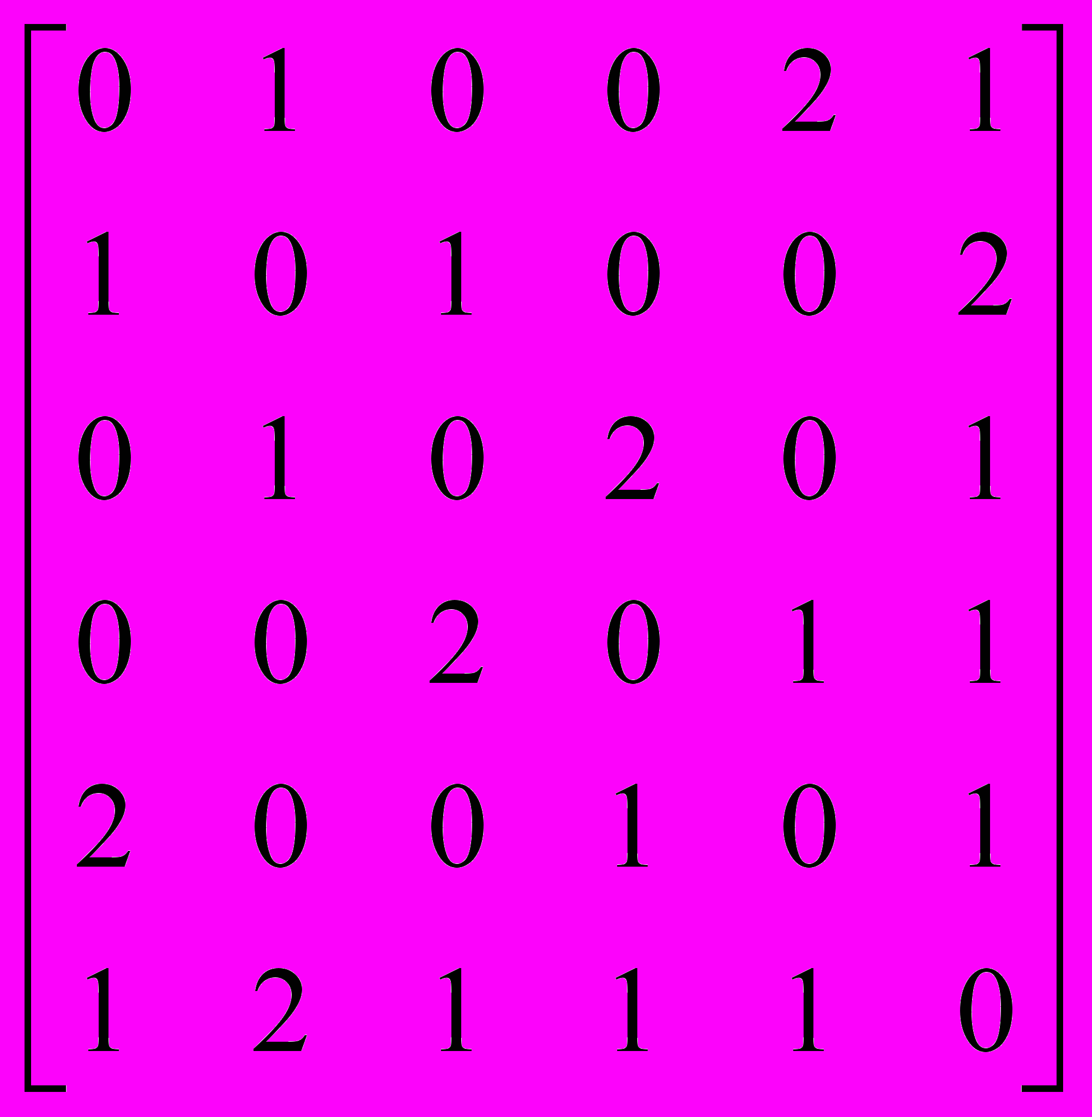 , A(G) =
, A(G) = 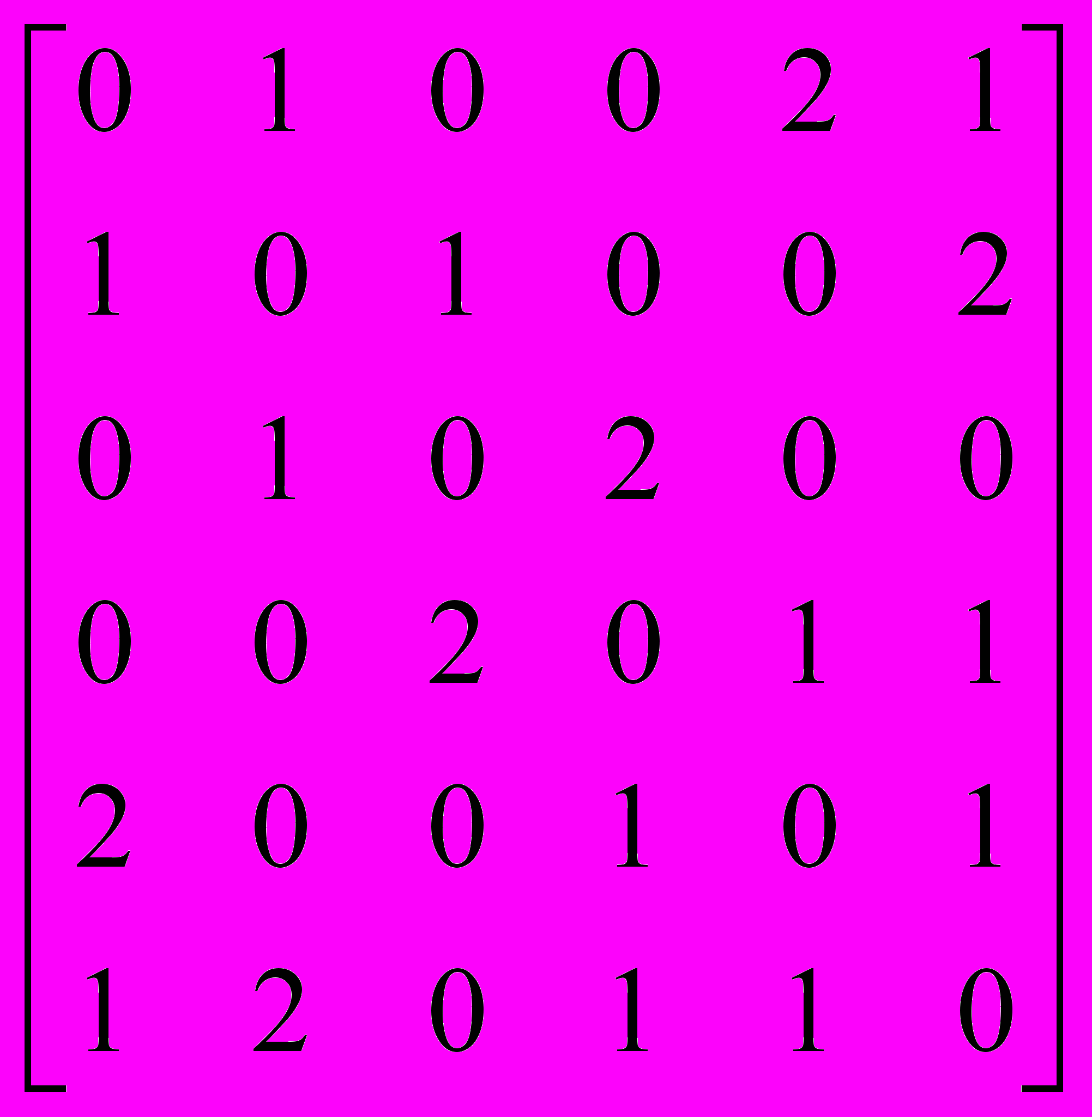
Теория алгоритмов.
- Имеется машина Тьюринга с внешним алфавитом А={a,1}, множеством внутренних состояний Q={q0,q1) и системой команд q1aq01, q11q11П (q0 – заключительное состояние). Определите, в какое слово перерабатывает машина каждое из следующих слов, если она находится в начальном состоянии q1 и обозревает указанную ячейку:
а. 1а11аа11 (обозревается ячейка 4, считая слева);
б. 11а111а1 (обозревается ячейка 2);
в. 1аа111 (обозревается ячейка 3);
г. 1111а11 (обозревается ячейка 4);
д 11а1111 (обозревается ячейка 3);
е. 1111111 (обозревается ячейка 4);
ж.11111(обозревается ячейка 5);
- Напишите программу для машины Тьюринга, которая бы к натуральному числу в десятичной системе счисления прибавляла единицу.
- Напишите программу для машины Тьюринга, которая бы от натурального числу в десятичной системе счисления отнимала единицу.
- Сконструируйте машину Тьюринга с внешним алфавитом A={a,1}, которая каждое слово длиной n в алфавите А1={1} перерабатывает в слово длиной n +1 в том же алфавите А (машина имеет два внутренних состояния q0 и q1).
- Постройте машины Тьюринга, которые правильно вычисляют следующие функции:
а. f(x) = x+1; б. O(x) = 0.
- Докажите, что функция
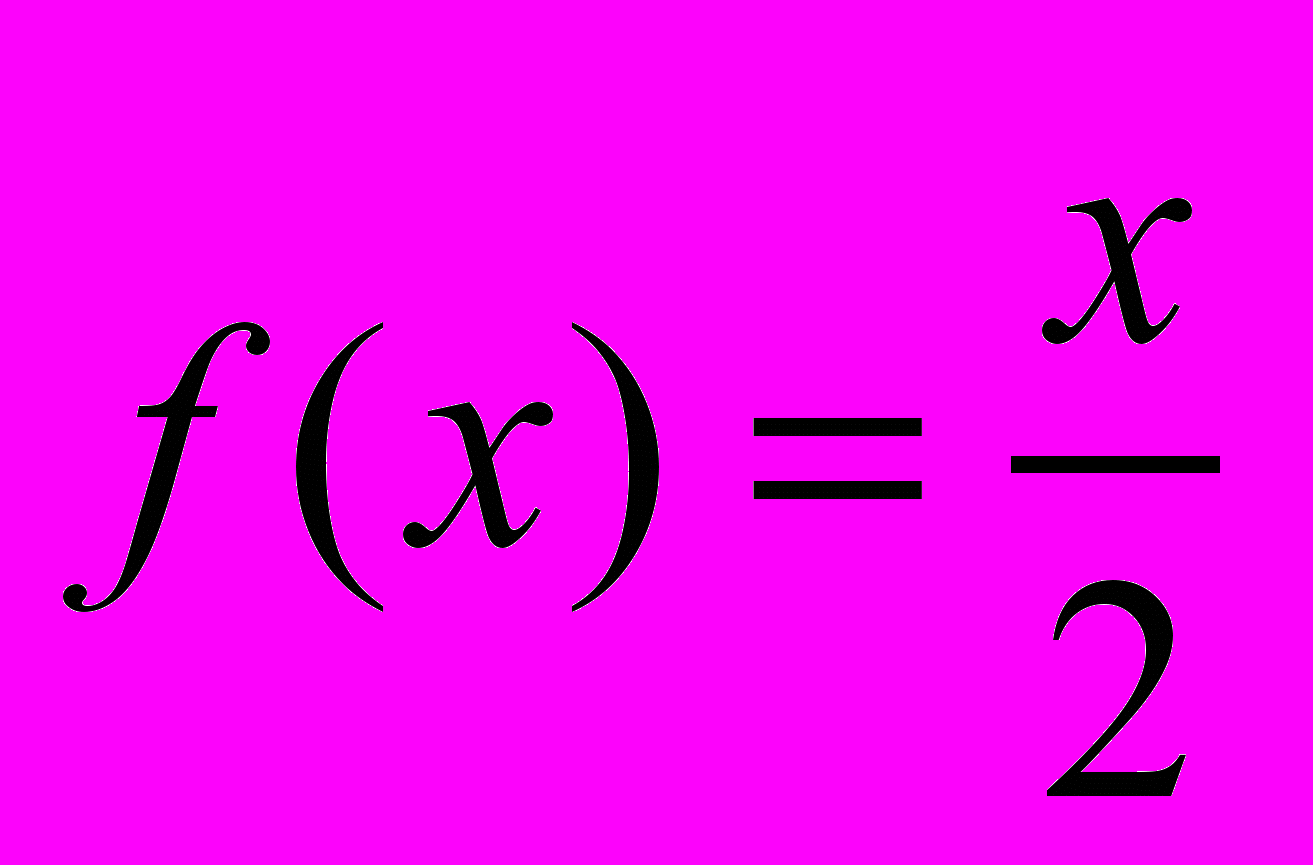 вычислима по Тьюрингу.
вычислима по Тьюрингу.
- Докажите, что следующие функции примитивно рекурсивны, руководствуясь непосредственно определением примитивно рекурсивной функции: a: (x) = n; b. (x) = n + x; c. (x,y) = x + y; d. . (x,y) = xy.
- Пусть для слов в алфавите А={a,b,c,d} заданы следующие марковские подстановки: а. abdc; б. bca; в. ddbb; г. acdc; д. cbd; е. abc; ж. cba; з. da; и. dacacd; к. ba; л. abd; Примените каждую из них к слову abcddacba.
- Нормальный алгоритм в алфавите {a,b,1}задается схемой: a1, b1. Примените его к слову: а. ababaa; б. bababbaa; в. aaa; г. bbbb; д. aabbb11; е. 11aab; ж. baaab1a; з. 111aab1; и. aabb; к.abbba; л. abaabbb.
- Нормальный алгоритм в алфавите {a,b,1}задается схемой: a1, b1, 11. Примените его к следующим словам : а. bbaab; б. bababab; в. aaaa; г. bbbbb; д. aabaabb; е. bbbaaa; ж. baaab1a; з. abbabba; и. baab; к.abbbbba; л. abbbaaab.
- Нормальный алгоритм в алфавите {a,b}задается схемой: aba, b., ab. Примените его к следующим словам: а. bbaab; б. bababab; в. aaaa; г. bbbbb; д. aabaabb; е. bbbaaa; ж. baaab1a; з. abbabba; и. baab; к.abbbbba; л. abbbaaab.
Теория автоматов.
1. Для регулярной грамматики G построить конечный автомат М.
G = ( N, T, P, S ), где N = { S, A, B }, Т = { a, b },
P = { S
 aA,
aA, S
 bB,
bB,S
 a,
a,A
 aA,
aA,A
 aS,
aS,A
 bB,
bB,B
 bB
bBB
 b,
b,B
 a}.
a}.2. Для конечного автомата М построить регулярную грамматику G.
М = (Q, Σ, t,
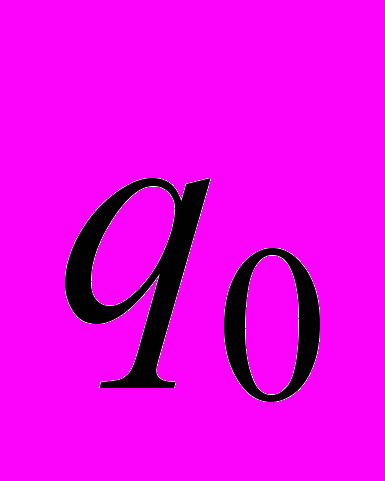 , F), где Q = {
, F), где Q = {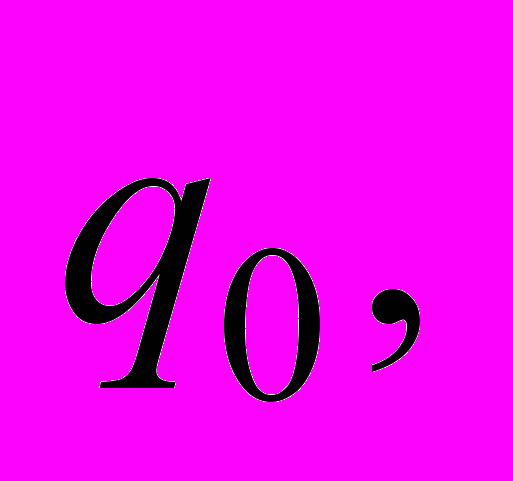
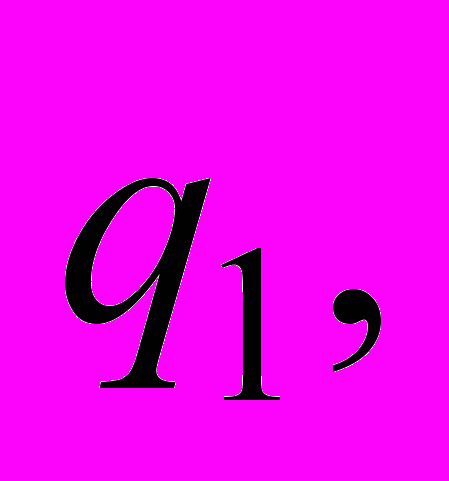
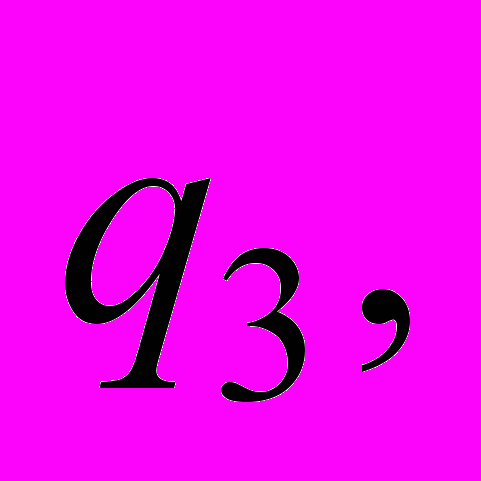
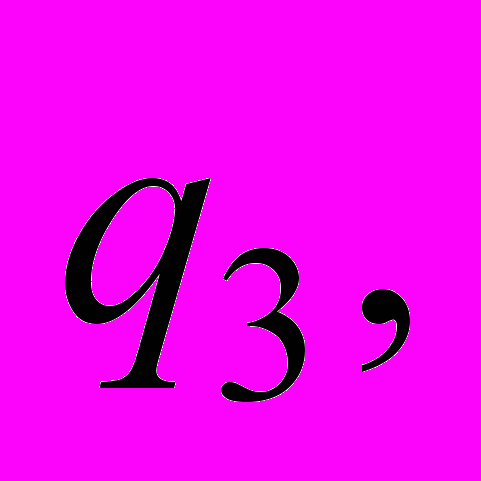
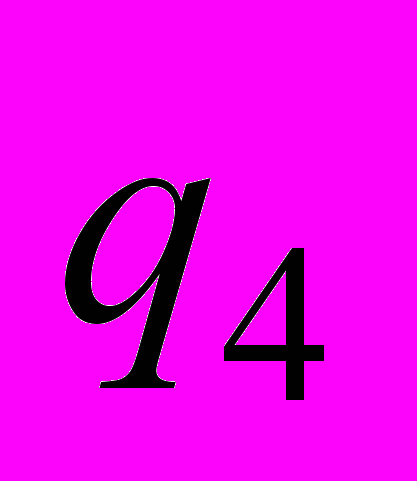 }, Σ = {0, 1), F = {
}, Σ = {0, 1), F = {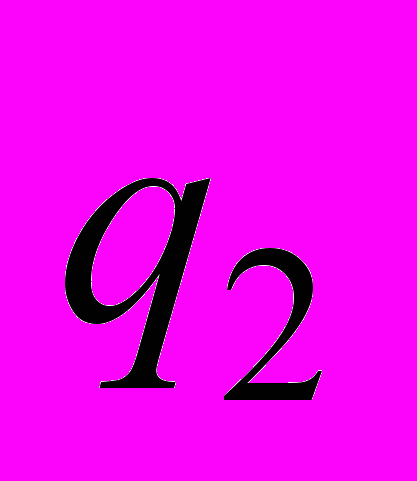 ,
, 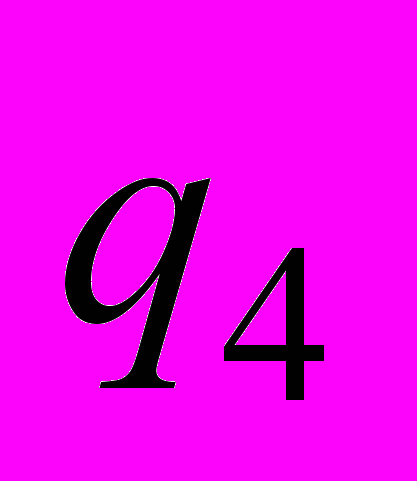 },
},t = {
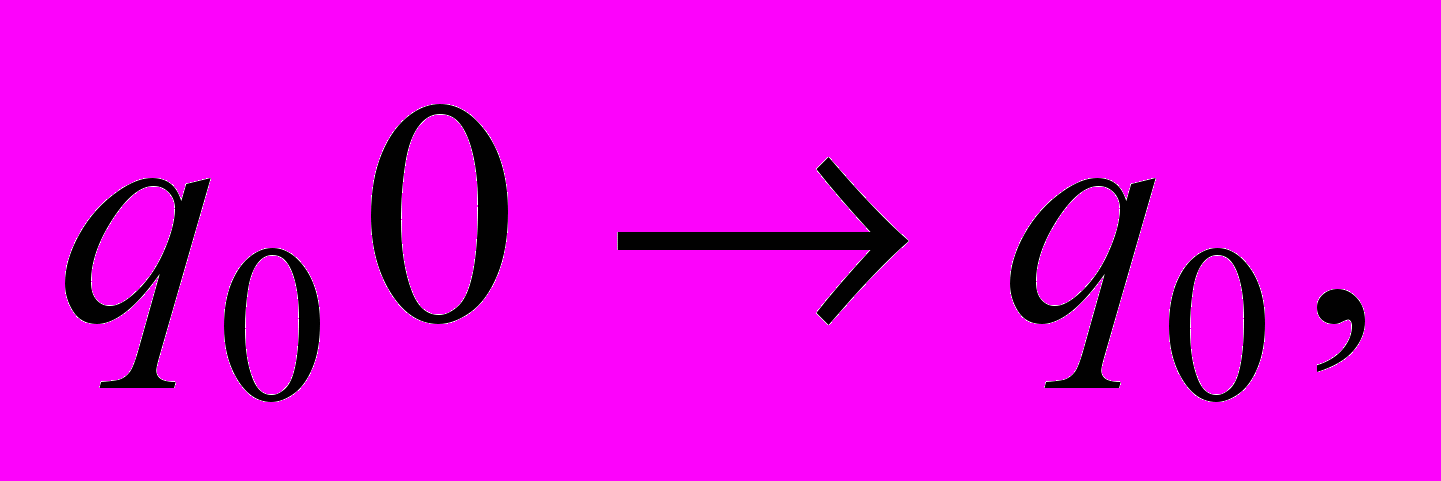
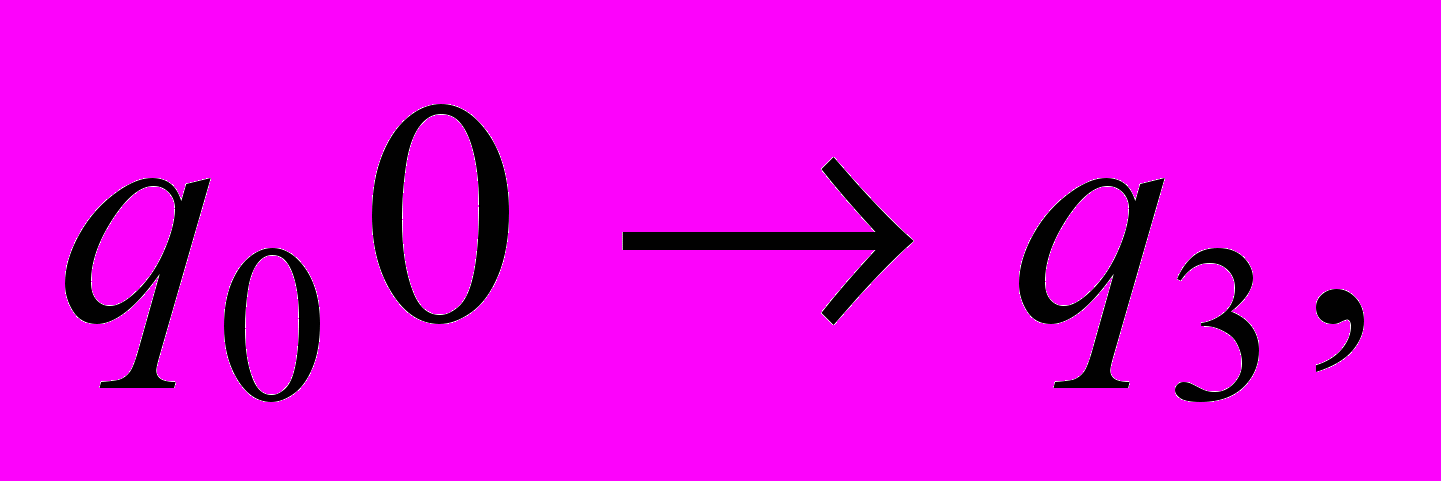
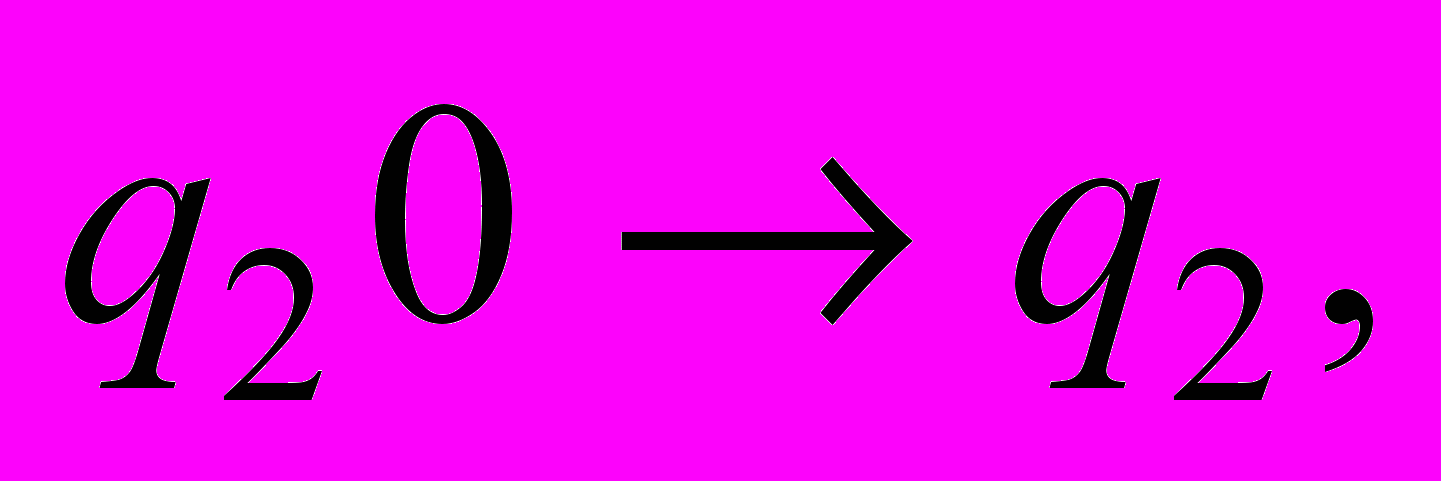
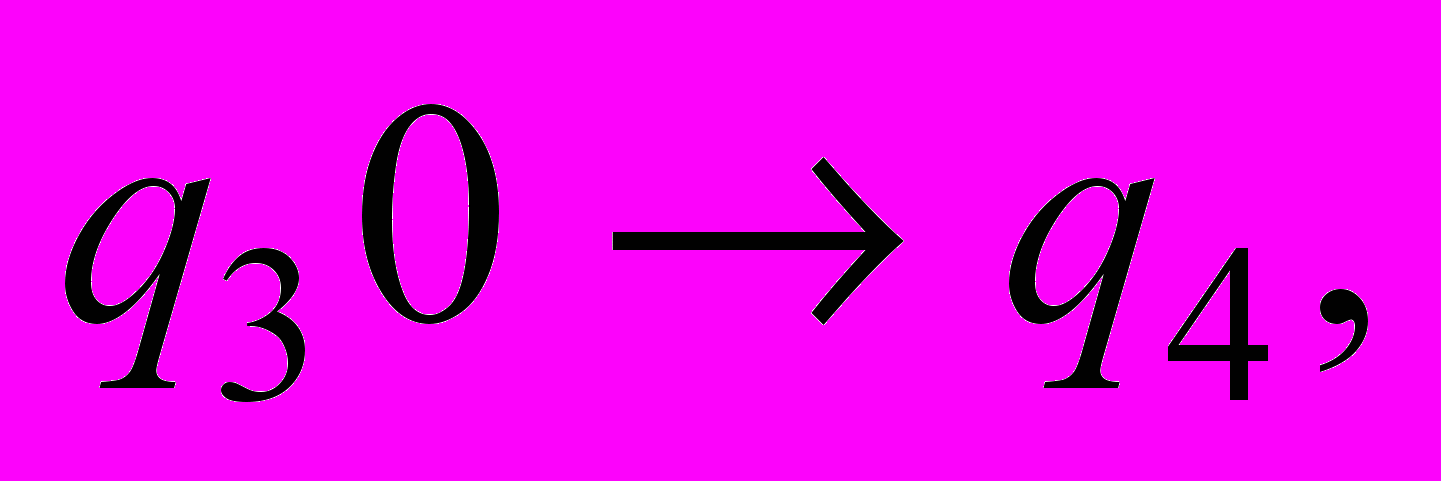
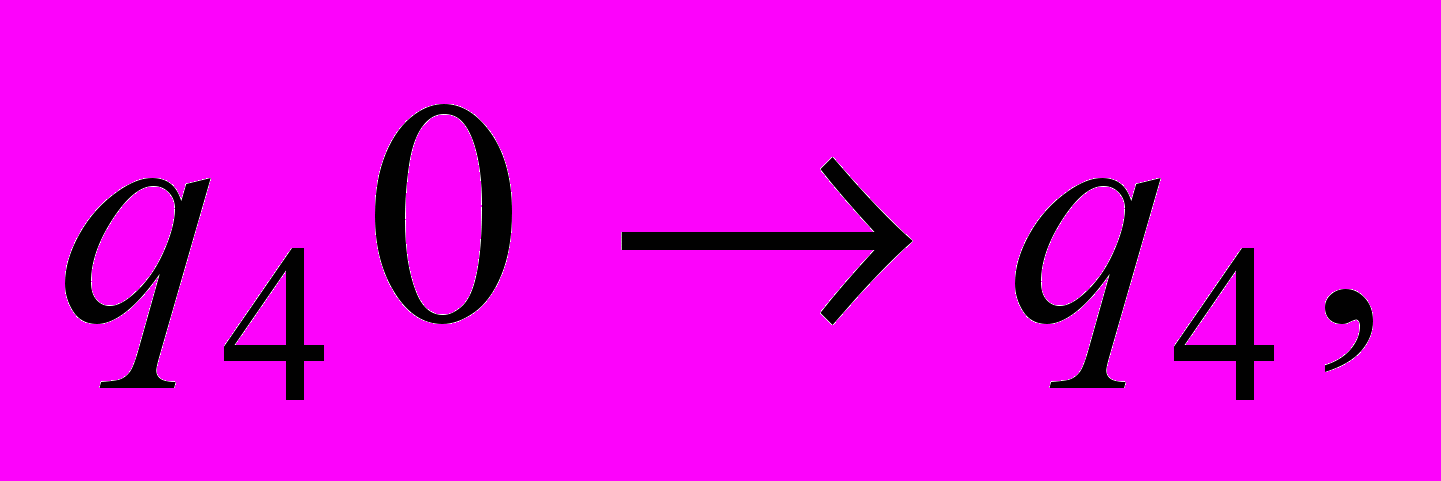

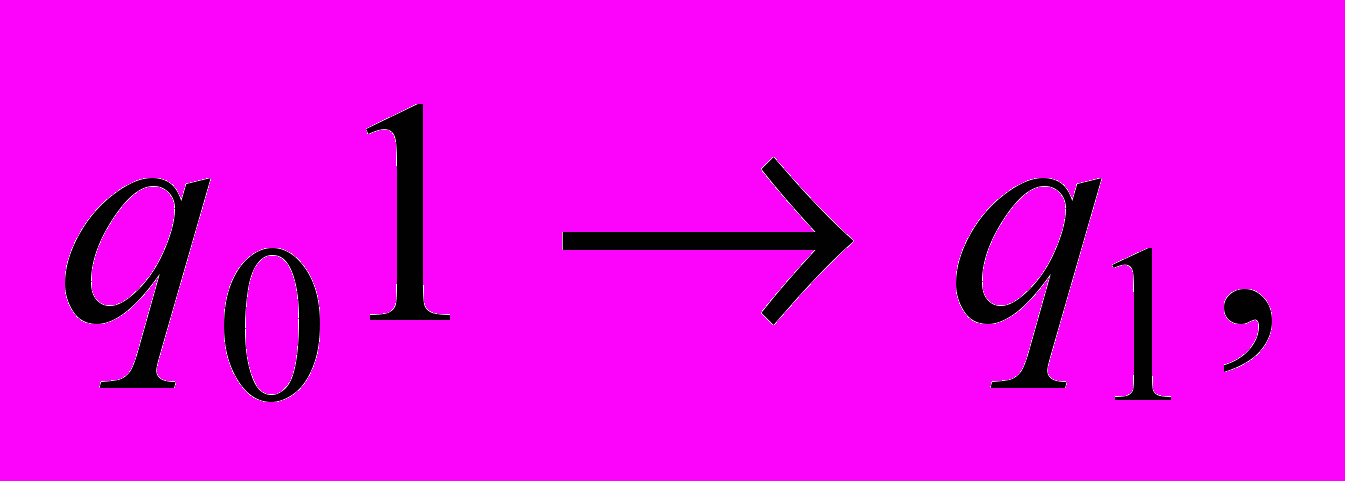

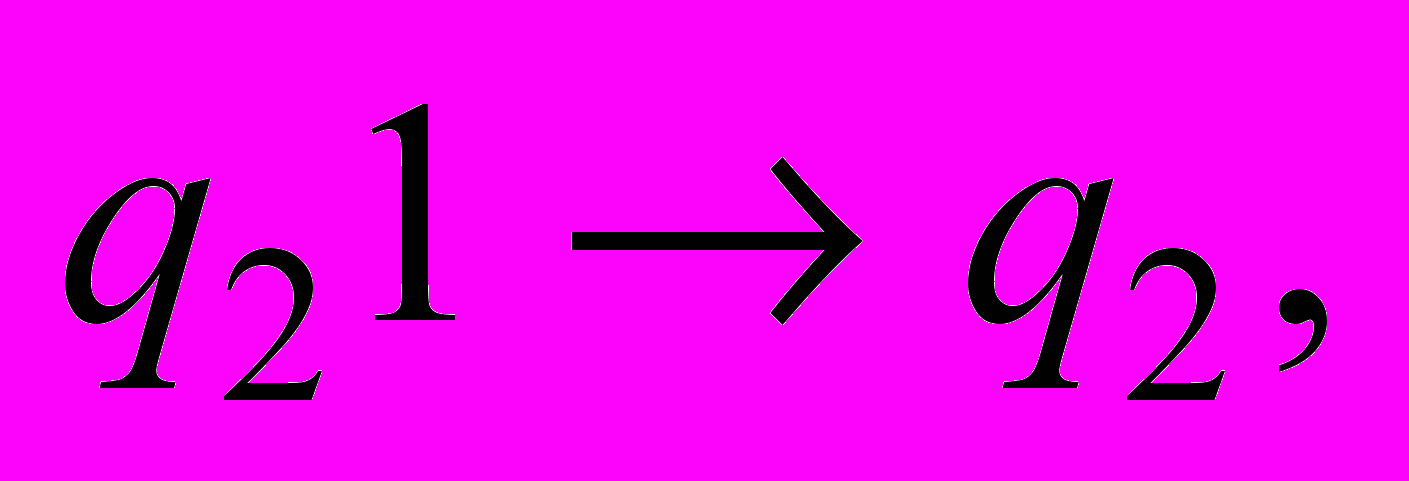
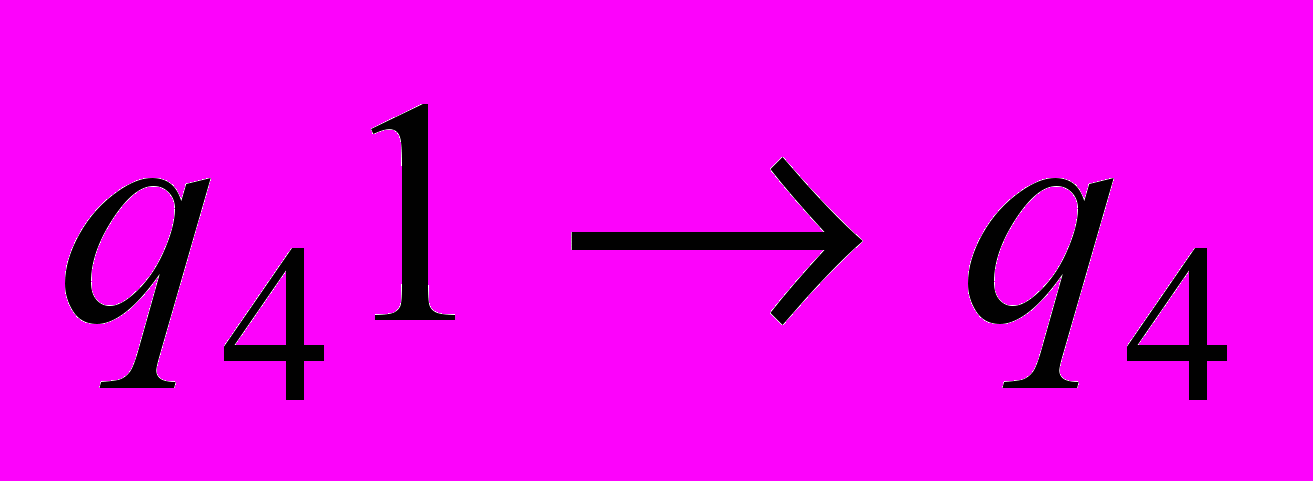 }.
}.ТИПОВЫЕ БИЛЕТЫ
ТИПОВОЙ БИЛЕТ 1
| 1 | Верно ли, что 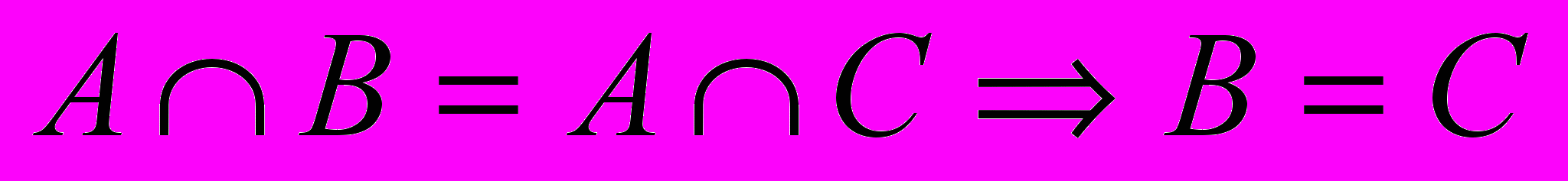 . . |
| 2 | Сколько положительных целых чисел меньших 100 не делятся на 8? |
| 3 | Доказать, что формула тождественно равна 0 или 1. 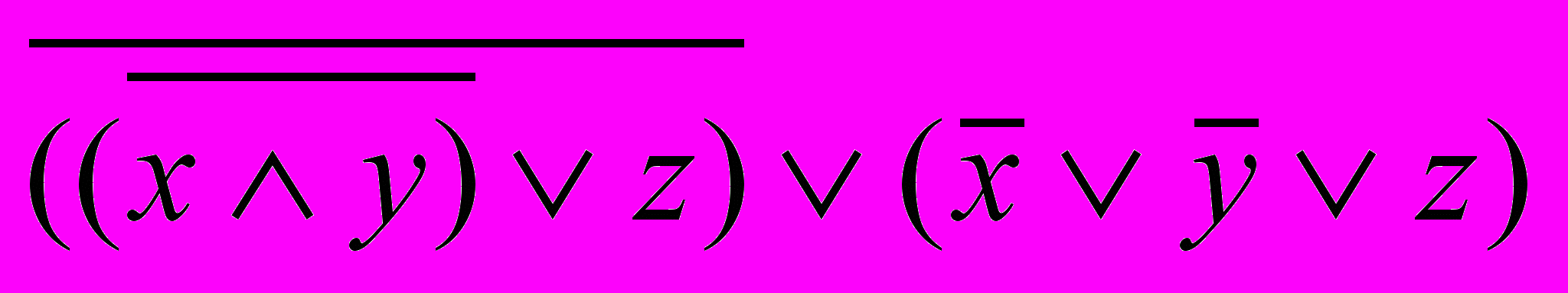 |
| 4 | Дано высказывание Q: ((A  B) B) C) C) A A (B (B C). C).Методом резолюции доказать, что Q├ C. |
| 5 | Если множество дизъюнктов S предложения унифицируемо, то найти НОУS ={{любит(w,(у))}, {любит(Джон, футбол)}}. |
| 6 | Определить минимальный путь из v1 в v7 в нагруженном орграфе D с числом дуг не более 5. С(D) = 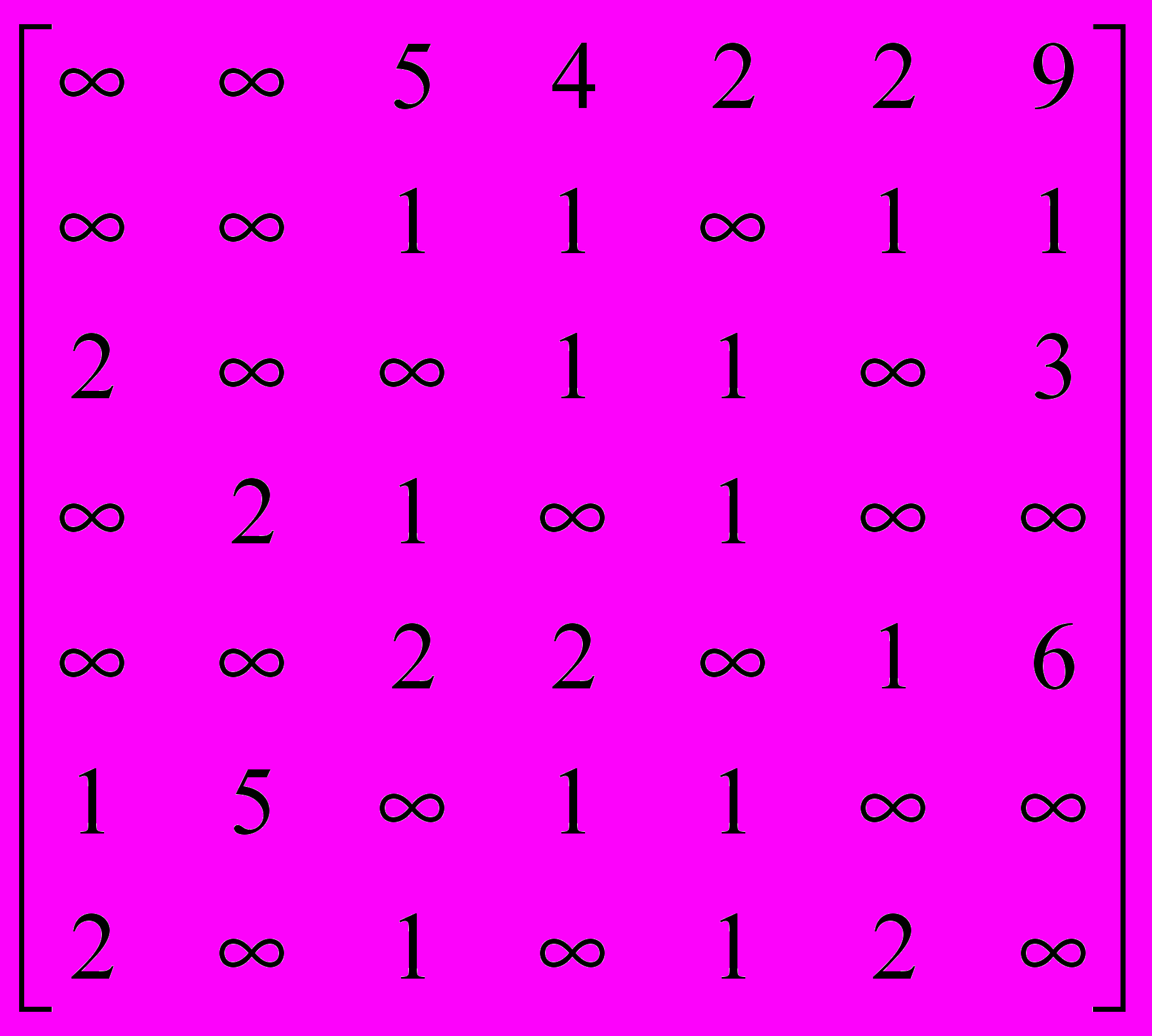 |
| 7 | Имеется машина Тьюринга с внешним алфавитом А={a,1}, множеством внутренних состояний Q={q0,q1) и системой команд q1aq01, q11q11П (q0 – заключительное состояние). Определите, в какое слово перерабатывает машина слово1а11аа11 (обозревается ячейка 4, считая слева), если она находится в начальном состоянии q1 и обозревает указанную ячейку: |
| 8 | Напишите программу для машины Тьюринга, которая бы к натуральному числу в десятичной системе счисления прибавляла единицу. |
| 9 | Докажите, что функция (x) = n примитивно рекурсивна, руководствуясь непосредственно определением примитивно рекурсивной функции. |
| 10 | Нормальный алгоритм в алфавите {a,b}задается схемой: aba, b., ab. Примените его к слову bbaab. |
| 1 | Найдите множество Х, удовлетворяющее следующим условиям A\X=A и AX=U |
| 2 | Сколько существует вариантов ответов на тест из 30 вопросов., если на каждый вопрос требуется ответ да или нет? |
| 3 | Записать в виде многочлена Жегалкина  |
| 4 | Записать предложение на языке логики предикатов . « Всякий человек имеет родителей». |
| 5 | Привести к ПНФ и далее записать предложение в СНФ (х)Р(х)(х)Q(х). |
| 6 | Проверить существуют ли в мультиграфе, заданном матрицей смежности, эйлеровы цепи и циклы, если да то найти их. A(G) = 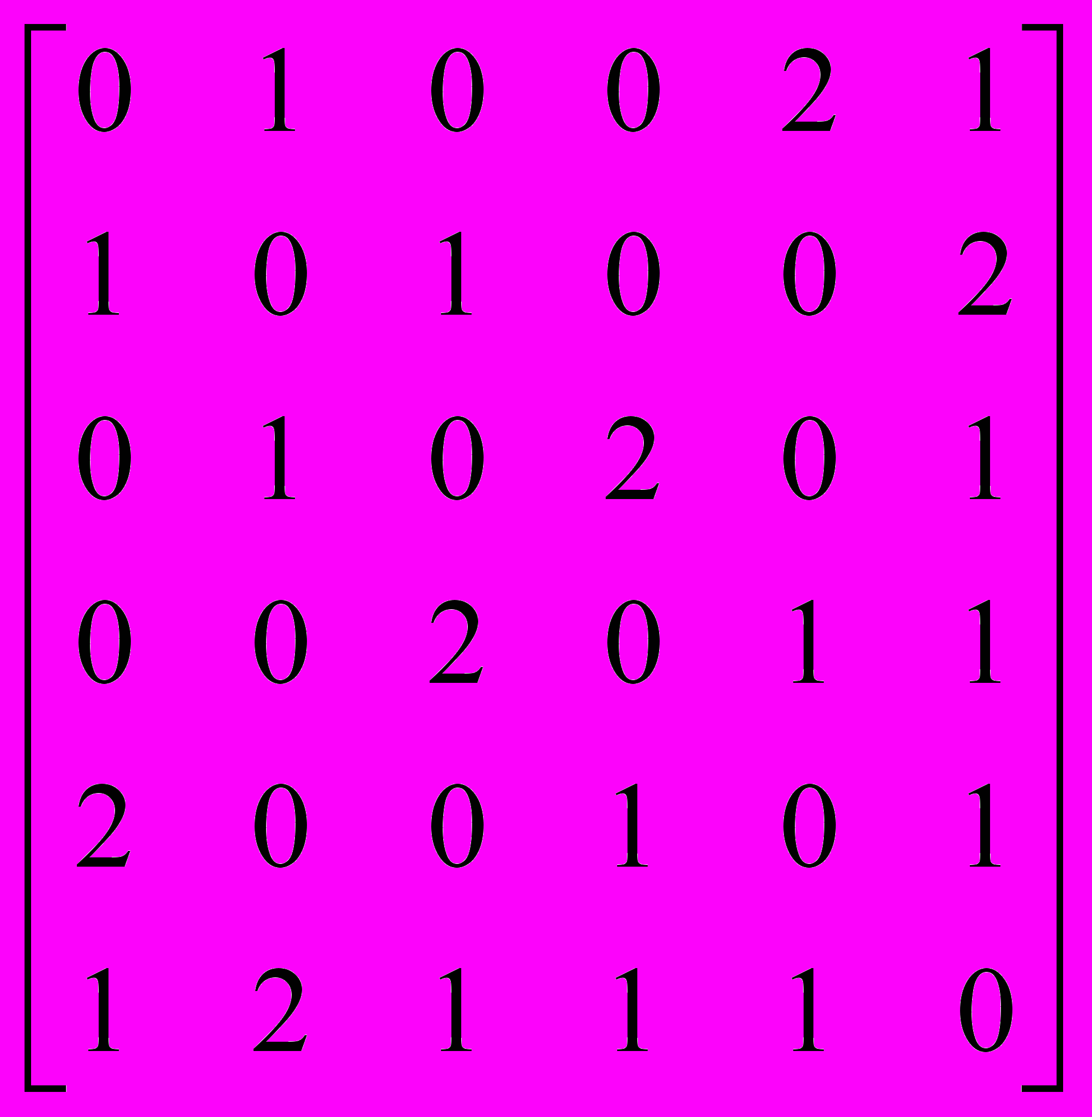 |
| 7 | Напишите программу для машины Тьюринга, которая бы от натурального числу в десятичной системе счисления отнимала единицу. |
| 8 | Докажите, что функция (x,y) = x+y примитивно рекурсивна, руководствуясь непосредственно определением примитивно рекурсивной функции. |
| 9 | Пусть для слова в алфавите А={a,b,c,d} задана марковская подстановка а. abdc. Примените её к слову abcddacba. |
| 10 | Для регулярной грамматики G построить конечный автомат М. G = ( N, T, P, S ), где N = { S, A, B }, Т = { a, b }, P = { S  aA, aA, S  bB, bB,S  a, a,A  aA, aA,A  aS, aS,A  bB, bB,B  bB bBB  b, b,B  a}. a}. |
ТИПОВОЙ БИЛЕТ 3
| 1 | . Существуют ли множества? A  B B , A , A C=, (A C=, (A B)\C= B)\C= |
| 2 | Если многоугольник имеет n сторон, то сколько у него диагоналей? |
| 3 | Известно, что х=1. Что можно сказать о значении: 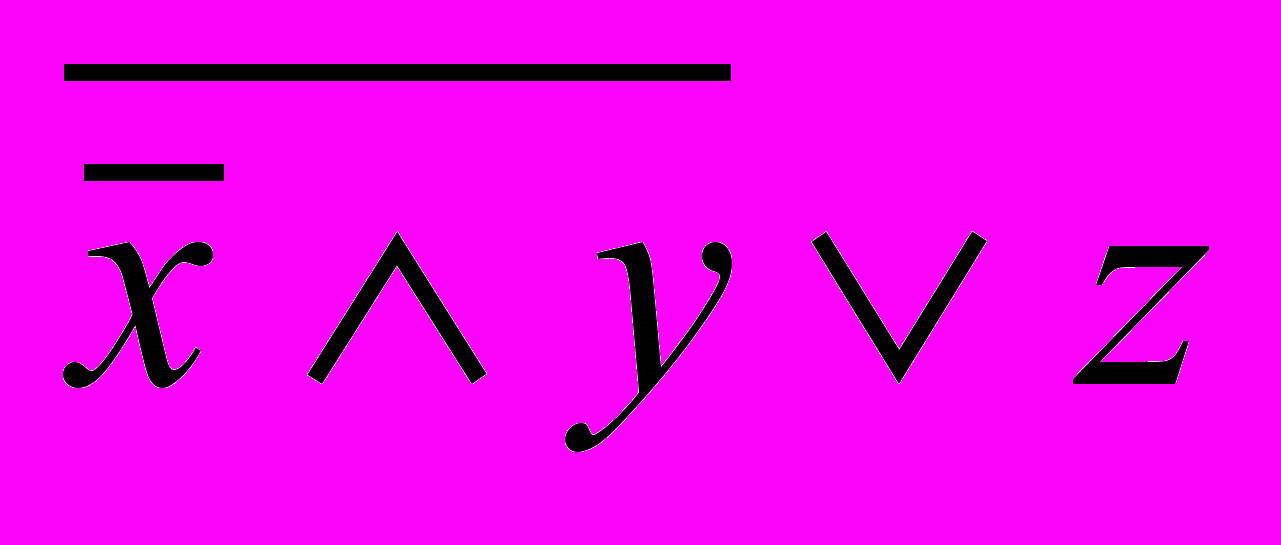 и и  . . |
| 4 | Доказать, что следующее высказывание является тавтологией (А→В)(АВ). |
| 5 | Записать на языке логики предикатов «Всякий ребенок имеет родителей» |
| 6 | 2. Найти минимальный путь из v1 в v6 методом «фронта волны».  |
| 7 | Докажите, что функция 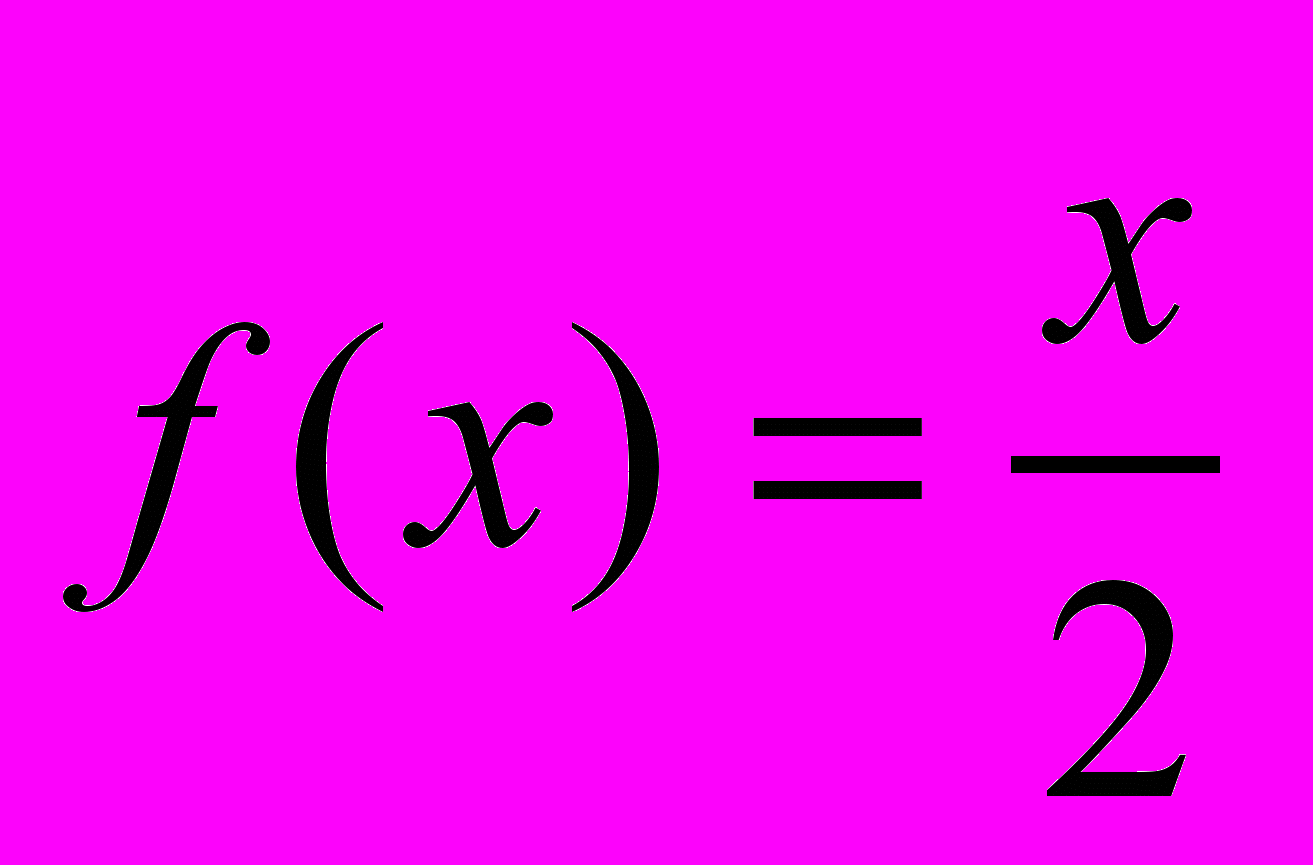 вычислима по Тьюрингу вычислима по Тьюрингу |
| 8 | Докажите, что функция (x) = n +х примитивно рекурсивна, руководствуясь непосредственно определением примитивно рекурсивной функции. |
| 9 | Пусть для слова в алфавите А={a,b,c,d} задана марковская подстановка da; . Примените её к слову abcddacba. |
| 10 | . Для конечного автомата М построить регулярную грамматику G. М = (Q, Σ, t, 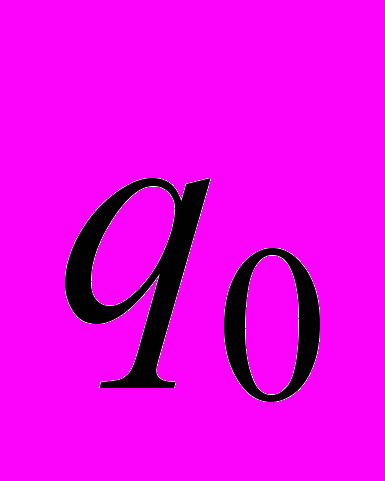 , F), где Q = { , F), где Q = {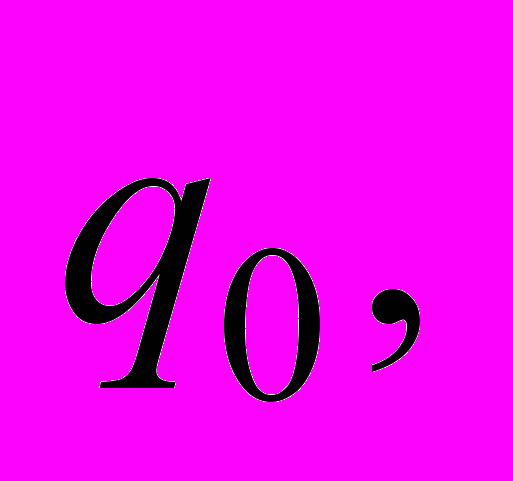 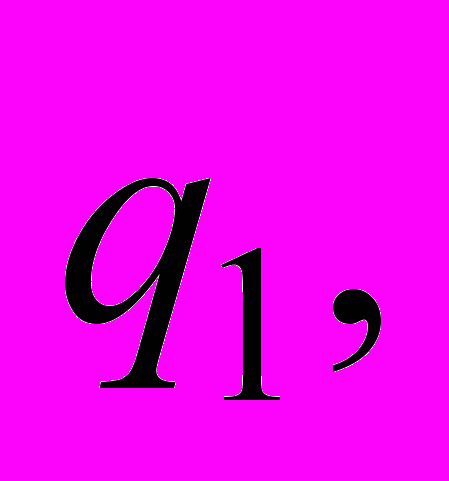 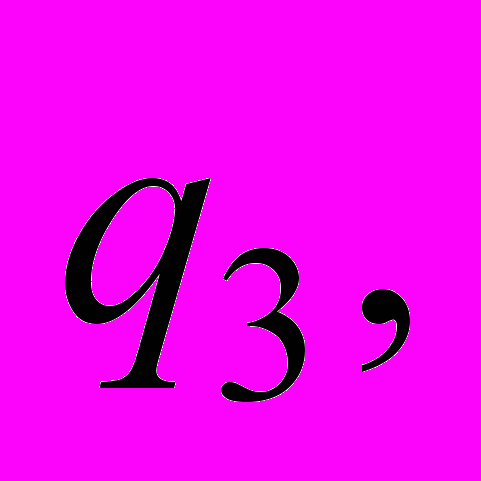 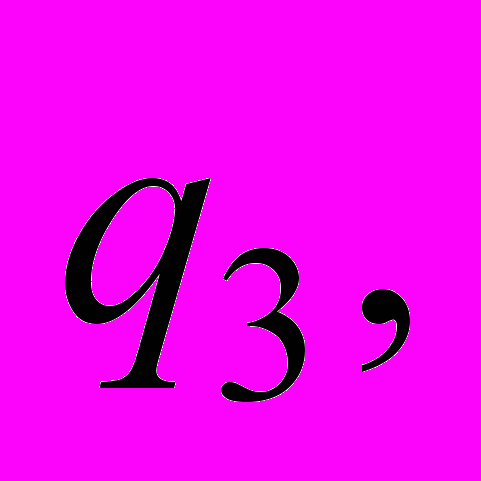 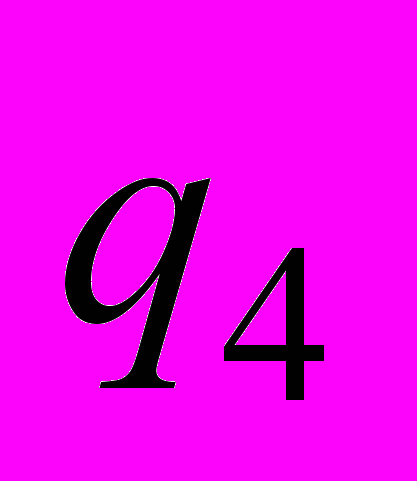 }, Σ = {0, 1), F = { }, Σ = {0, 1), F = {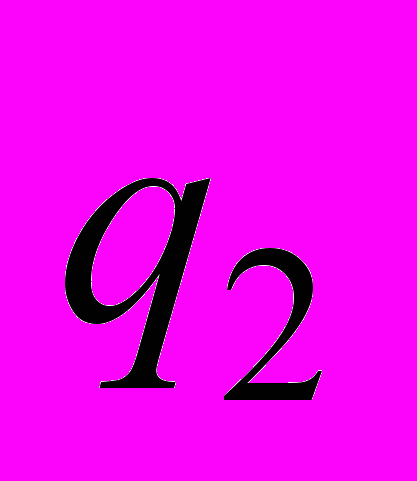 , , 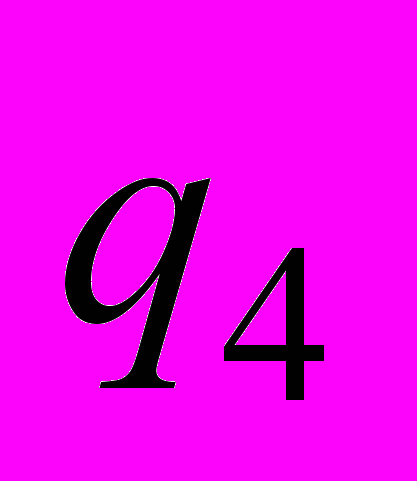 }, },t = { 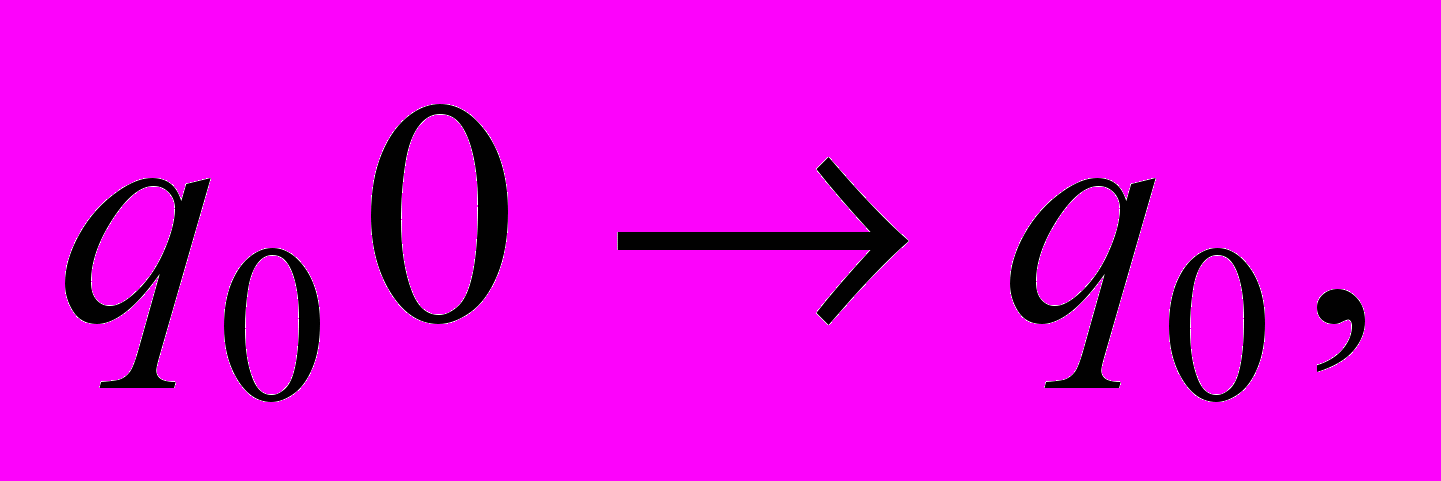 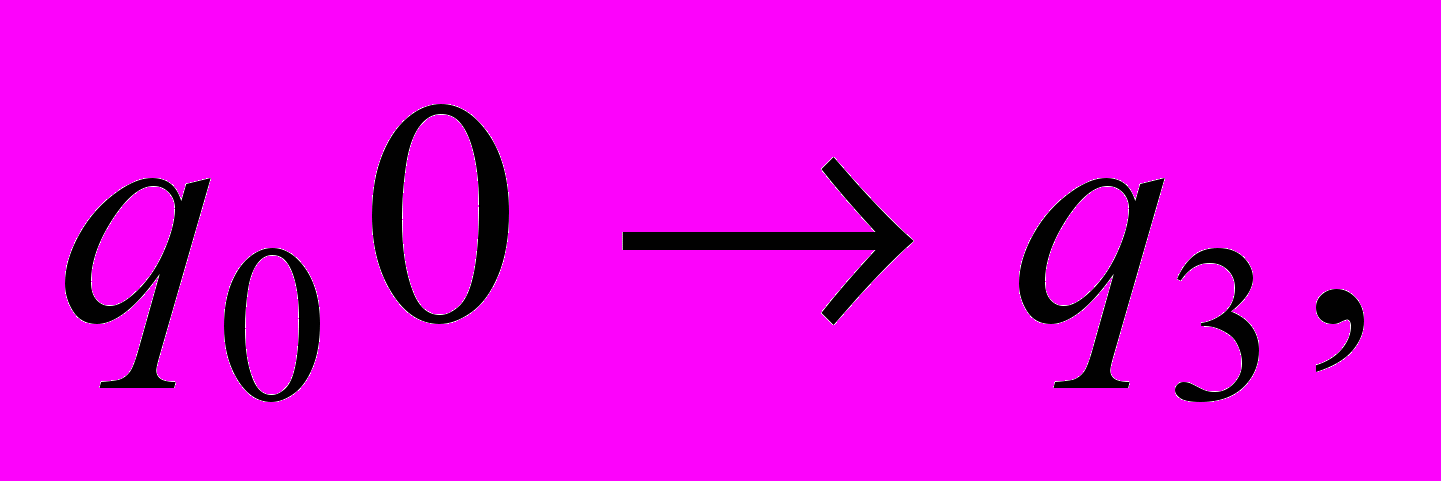 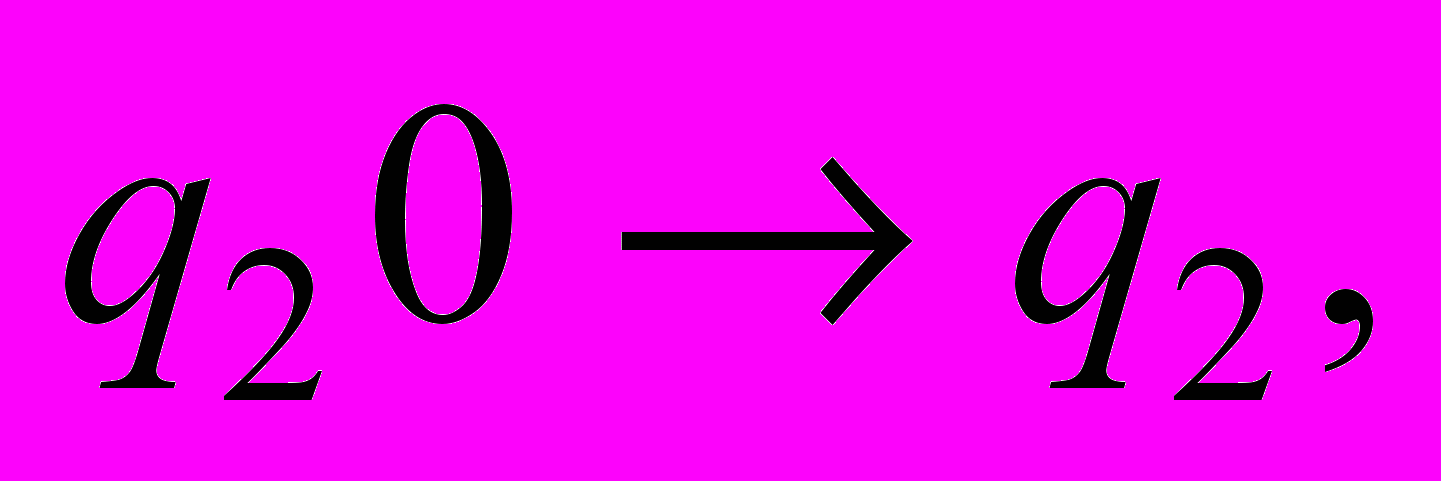 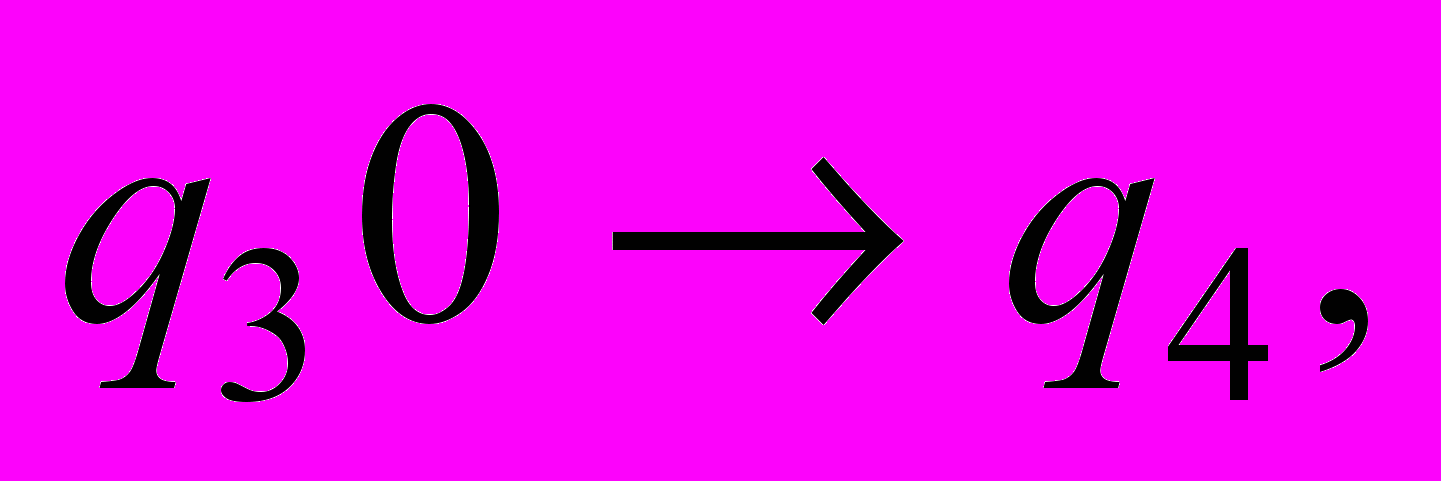 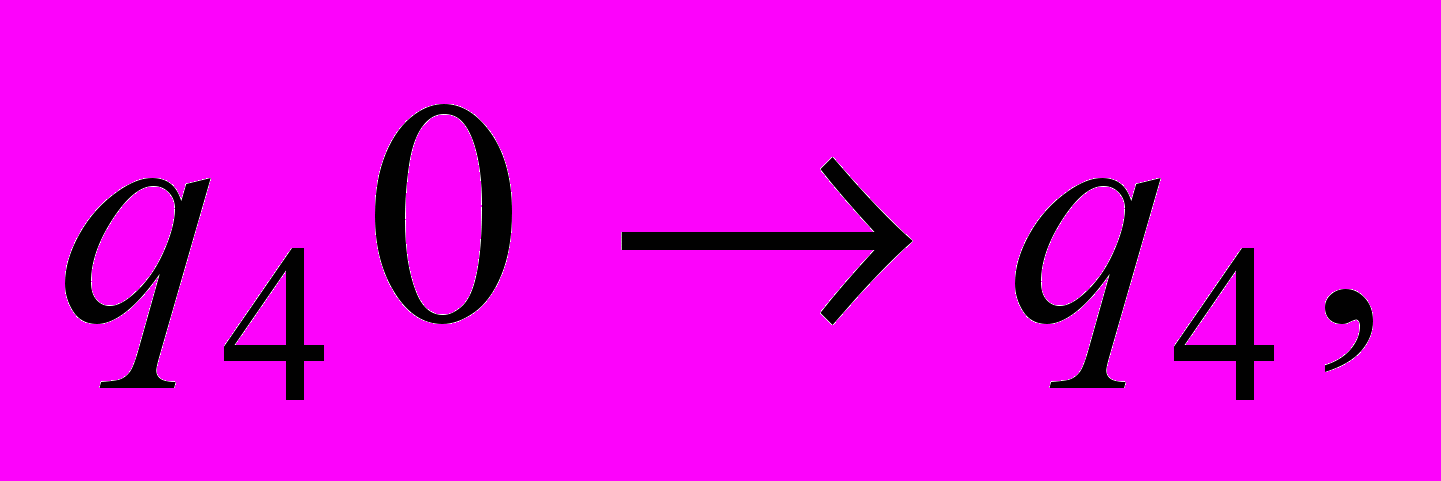  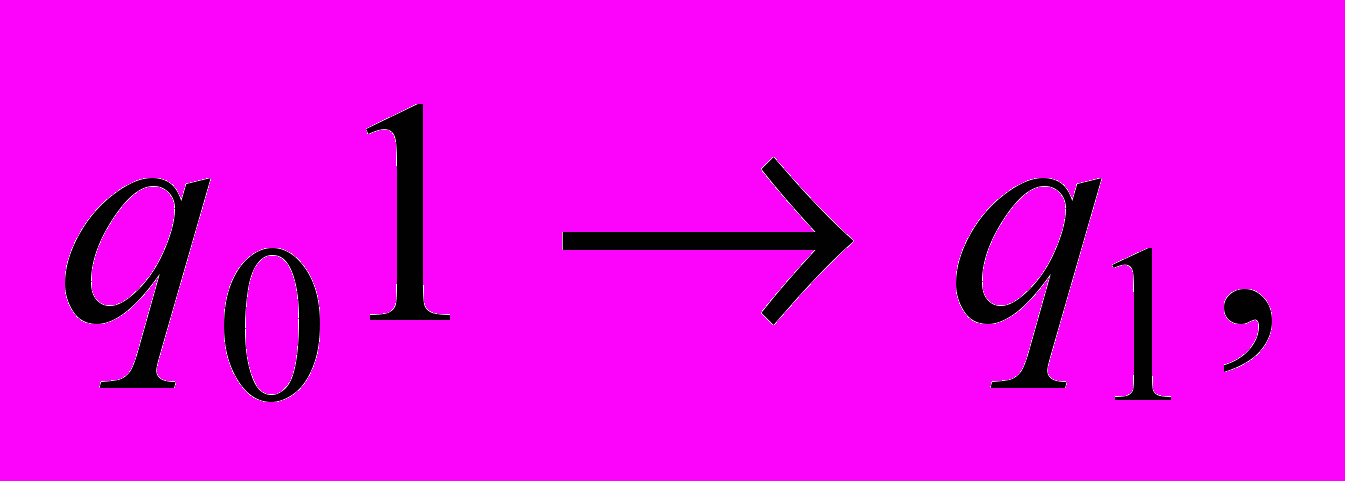  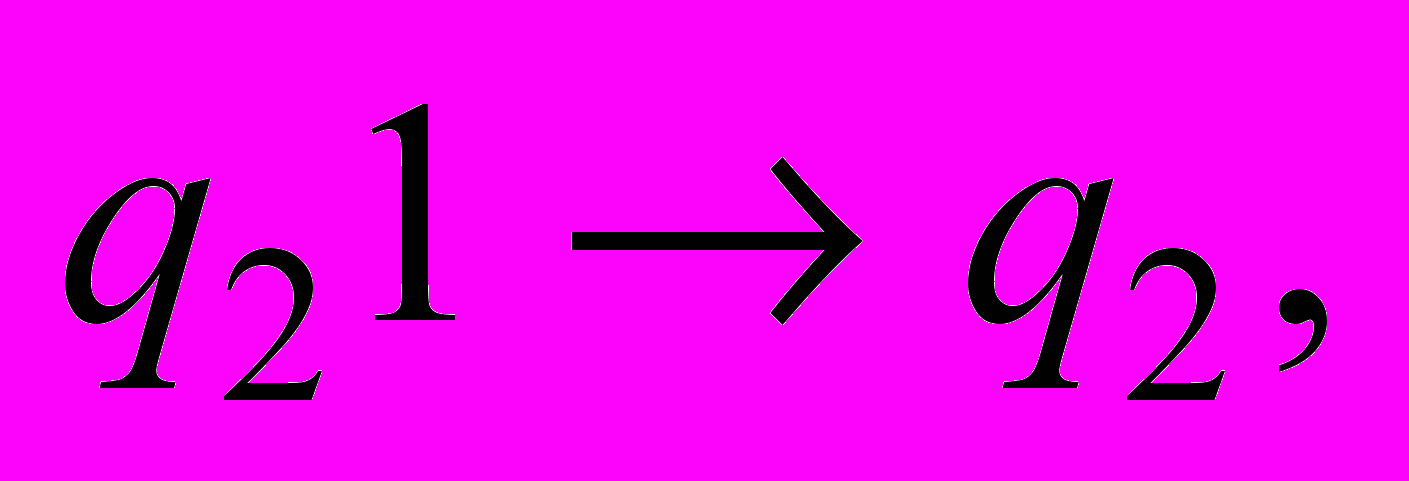 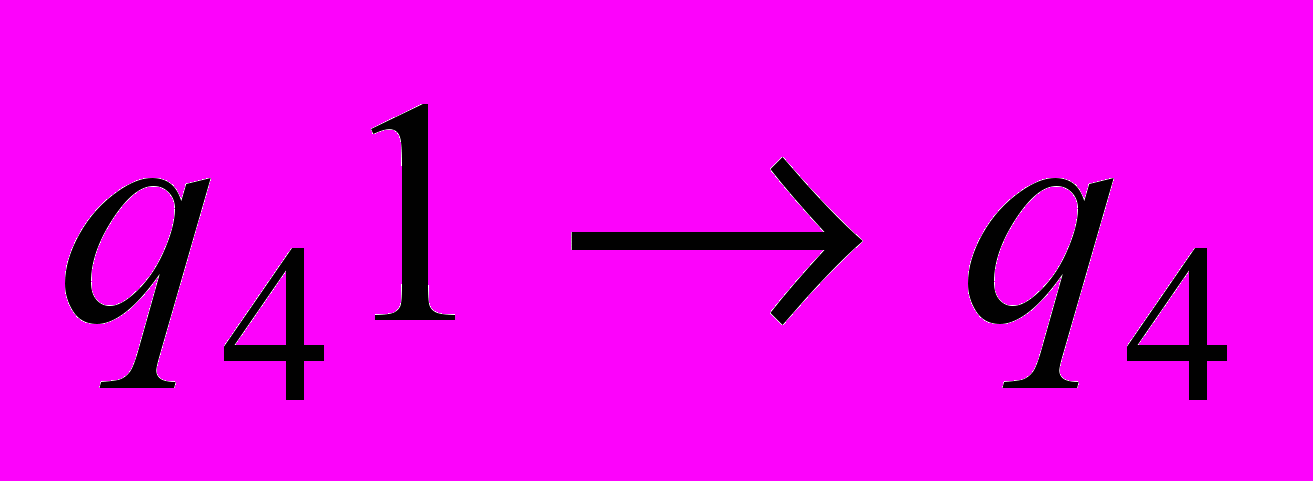 }. }. |
УЧЕБНО-МЕТОДИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ДИСЦИПЛИНЫ.
Базовые учебные пособия.
- 20. Нефедов В.Н., Осипова В. А. Курс дискретной математики. М.: Изд. МАИ. 1992. 264 с.
- С.В. Судоплатов, Е.В. Овчинникова Элементы дискретной математики. М.: ИНФРА-М, Новосибирск: Изд-во НГТУ 2002. 280 с.
- В.И. Игошин Математическая логика и теория алгоритмов. М: Издательский центр «Академия», 2004.- 448 с.
- С.Д. Шапорев Математическая логика. Курс лекций и практических занятий. СПб
БХВ-Петербург, 2005.-416 с.
- Куликов Л. Я., Москаленко А. И., Фомин А. А. Сборник задач по алгебре и теории чисел. М.: Просвещение. 1993. 288 с.
- Лавров И. А., Максимова Л. Л. Задачи по теории множеств, математической логике и теории алгоритмов. М.: ФИЗМАТЛИТ. 2001. 256 с.
- Игошин В.И. Задачи и упражнения по математической логике и теории алгоритмов. М. Академия. 2005.- 304 с.
