Методы и средства анализа безопасности программного обеспечения

Вид материала

Документы

Содержание 7.6.Метод расчета вероятности наличия РПС на этапе испытаний программного обеспечения вычислительных задач Дано: алгоритм А, подлежащий реализации программой П, и требуемая достоверность результатов тестирования Р Требуется определить. 7.6.2.Обоснование состава множестваинформативных характеристик 7.6.3.Алгоритмы приближенных вычислений вероятностныххарактеристик наличия в программах РПС Дано: совместная плотность распределения вероятностей w 7.6.4.Обоснование критериев принятия решенияо наличии в программе РПС Дано: Р=F Точность аналитического вычисления ВХ. Ограниченность числа испытаний (прогонов) программы. Закон распределения входных случайных величин

Подобный материал:

• Рабочая программа учебной дисциплины (модуля) case-средства проектирования программного, 143.56kb.
• Программа-минимум кандидатского экзамена по специальности 05. 13. 19 «Методы и системы, 67.78kb.
• Кафедра системного анализа, 34.57kb.
• Программа «Математические проблемы защиты информации», 132.24kb.
• Направление 090305 «Информационная безопасность автоматизированных систем» Информационная, 17.19kb.
• § Модели угроз безопасности программного обеспечения, 158.47kb.
• Ейрокомпьютерные системы, технология разработки программного обеспечения, сети ЭВМ, 24.18kb.
• Information technology. Security techniques. Evaluation criteria for it security Security, 4433.86kb.
• Вопрос №3 Принципы проектирования информационного обеспечения программного комплекса, 2541.91kb.
• Программа вступительного экзамена в аспирантуру по специальной дисциплине 05. 20., 94.72kb.

7.6.Метод расчета вероятности наличия РПС на этапе испытаний программного обеспечения вычислительных задач

7.6.1.Постановка задачи

С точки зрения технологической безопасности тестирование должно позволять не только декларировать факт отсутствия в проверенных частях программных комплексов РПС, но и получать количественные характеристики, чаще всего вероятностные, существования таких дефектов в непроверенных программных компонентах. Данное утверждение справедливо для больших комплексов программ, полностью проверить все логические ветки которых не представляется возможным. К таким программам, в частности, можно отнести комплексы управления сложным технологическим процессом.

При исследовании сложных комплексов программ возникают существенные трудности использования известных методов детерминированного тестирования, связанные с необходимостью генерации входных наборов данных и расчета эталонных выходных данных. Использование метода стохастического тестирования упрощает генерацию входных данных, однако необходимость расчета эталонов сохраняется. Существенным при этом является то, что принципиально невозможно создать единый алгоритм расчета эталонов для различных тестируемых программ, что особенно характерно для программ, реализующих вычислительные алгоритмы.

Сущность вероятностного тестирования заключается в следующем. Исследуемая программа реализуется на наборах входных данных, представляющих собой случайные величины, распределенные по некоторому закону F(x). Для некоторого множества контрольных точек определяются вероятностные характеристики (ВХ) случайных величин, являющихся для этих точек выходными данными. Полученные ВХ сравниваются с эталонными ВХ, рассчитанными для данного закона распределения входных величин по заданному в спецификациях программы алгоритму, который данная программа реализует. В зависимости от степени совпадения экспериментально определенных ВХ с эталонными делается вывод об отсутствии в программе дефектов, преднамеренно внесенных на этапе ее создания. Необходимо отметить, что данный метод позволяет выявлять любые дефекты программы, в том числе и случайные ошибки. Однако использование стохастического тестирования наиболее целесообразно для тех участков сложных программных комплексов, для которых детерминированные методы требуют существенных по объему затрат на подготовку тестовых наборов данных. В то же время применение на этапе отладки программ более простых методов позволяет практически ликвидировать вероятность проявления случайных ошибок после завершения отладки и представления программного обеспечения на испытания.

Область применения метода вероятностного тестирования программ определяется в основном границами применимости математического аппарата, используемого для расчета эталонных вероятностных характеристик. Для программ, реализующих вычислительные функции, задача расчета вероятности наличия в программе РПС формулируется следующим образом [ЕУ].

Дано: алгоритм А, подлежащий реализации программой П, и требуемая достоверность результатов тестирования Р₀ (вероятность наличия РПС в нетестируемых ветвях программы при заданном числе испытаний).


Требуется определить.

• последовательность законов распределения F₁(x),...,F_n(x), j=1,..., входных величин Х={x_j}, при которой с вероятностью Р_пр гарантируется отсутствие в тестируемой программе РПС; при этом с вероятностью Р₀ такие дефекты могут иметь место в нетестированных участках программы;
  
• множество контрольных точек (КТ_i), i=1,...,k, в которых определяется экспериментальное распределение выходных величин;
  
• множество G_i вероятностных характеристик, снимаемых с заданного множества КТ;
  
• множество величин L_i таких, что если существует i, что
  (G_iэкс-G_iэт>L_i), то программа содержит дефекты с вероятностью Р₀ или не содержит их с вероятностью Р_пр.
  

Для решения данной задачи необходимо использовать методику, основанную на модификации метода вероятностного тестирования и позволяющую последовательно решить следующие частные задачи: определить множество информативных характеристик G_i случайных величин, снимаемых с некоторого множества КТ_i исследуемой программы; определить критерии принятия решения о наличии дефектов в программе П, обеспечивающих заданную достоверность такого решения.

7.6.2.Обоснование состава множества
информативных характеристик

Выбор информативных ВХ случайных величин G_i должен производиться с учетом двух основных факторов:

• выбранные ВХ должны существенно изменять свои значения при наличии в программе РПС;
  
• ВХ должны относительно легко вычисляться при экспериментальных исследованиях программы.
  

Поскольку информативные характеристики должны реагировать на наличие в программе закладок, изменяющих основной алгоритм функционирования или инициирующих изменение исходных данных (промежуточных или конечных результатов), следовательно, необходимо определить класс функций, которые получаются из исходной под воздействием программной закладки. К сожалению, РПС сами нуждаются в дополнительном исследовании и классификации, могут искажать реализуемую функцию в таком широком диапазоне, что однозначно предсказать ее искаженный вид просто невозможно. Поэтому для количественной оценки информативности той или иной ВХ целесообразно хотя бы приблизительно определить ожидаемый вариант воздействия дефекта на исследуемую программу.

С точки зрения удобства экспериментального вычисления наиболее простой характеристикой является значение функции распределения в одной точке. Вычисление этой характеристики сводится к подсчету значений выходной величины, попавших в заданный интервал. Вычисление этой ВХ для тех контрольных точек программы, где критерием перехода на ту или иную ветвь является значение функции, сводится к подсчету числа прохождений по этим ветвям. Например, экспериментальные исследования программ, входящих в специальное ПО, реализующего комбинационные алгоритмы выбора предпочтений, показали, что для программ такого класса частота прохождения различных ветвей при заданном законе распределения входных данных является достаточно устойчивой информативной характеристикой. Если при этом еще фиксировать временные интервалы прохождения различных путей программы, которые могут существенно отличаться друг от друга, то время выполнения также может использоваться в качестве информативной характеристики.

ссылка скрыта BEST rus DOC FOR FULL SECURITY

Для вычислительных программ, обладающих достаточно простой ациклической структурой, но реализующих сложные вычислительные функции, например, вычисления полиномов различной степени в приближенных расчетах, в качестве вероятностных характеристик могут использоваться начальные моменты законов распределения входных данных



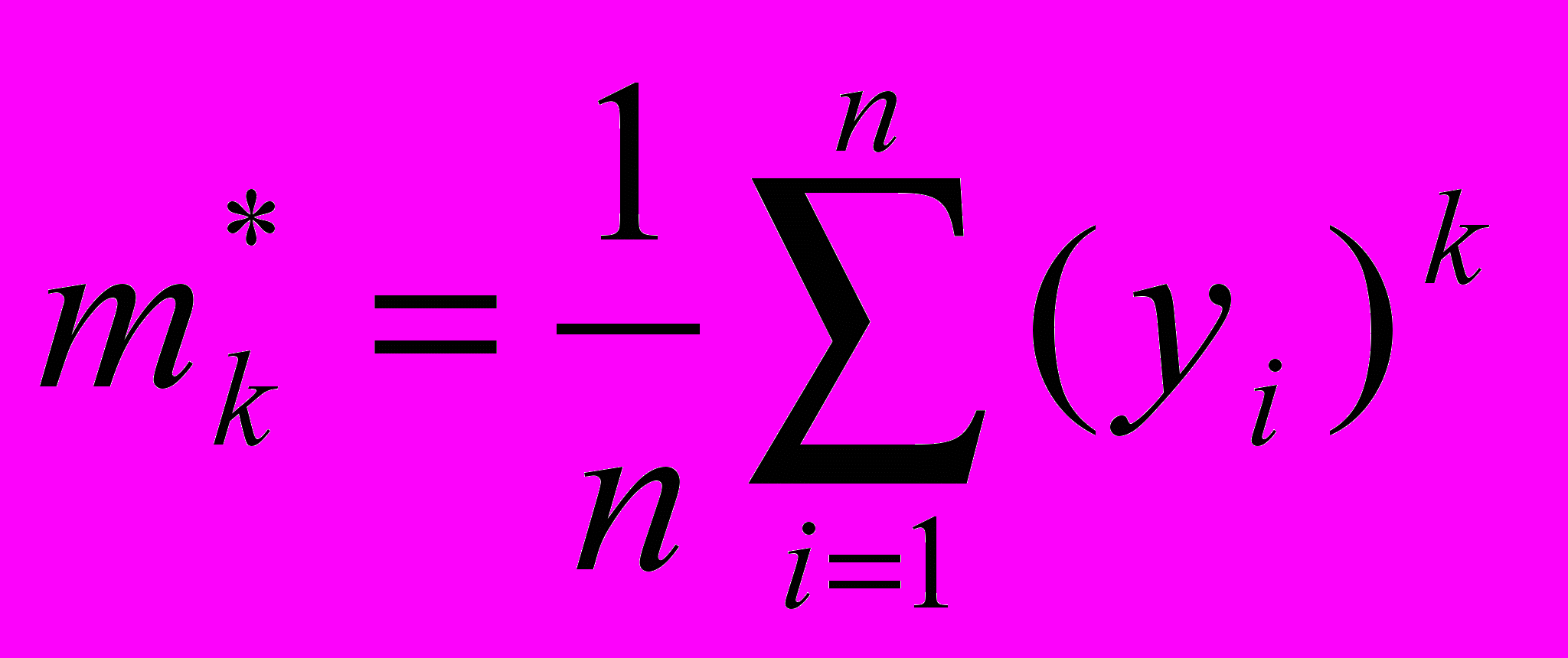
где y_i - значения входной величины при i-том испытании (прогоне программы);

m_k^* - начальный момент, полученный при проверке программы;

n - число прогонов программы.

7.6.3.Алгоритмы приближенных вычислений вероятностных
характеристик наличия в программах РПС

В основу алгоритмов приближенных вычислений ВХ положен принцип расчета ВХ по функциям распределения выходных и промежуточных величин. При этом законы их распределения вычисляются как распределения функции от случайных аргументов [ЕУ].

Задача функционального преобразования непрерывных случайных величин формируется следующим образом.

Дано: совместная плотность распределения вероятностей w_n(x₁,...,x_n) непрерывных случайных величин ₁,...,_n и совокупность функций f₁,...,f_m от n переменных. С помощью этих функций определены m случайных величин h₁=f₁(x₁,...,x_n),...,h_m=f_m(x₁,...,x_n), где x_i – значения случайных величин _i.

Необходимо: определить закон распределения каждой полученной случайной величины h_j и их совместную плотность W_m(y₁,...,y_m), где y_i - значения случайных величин h_j.

Решение этой задачи точными методами [КК] даже для одномерного случая возможно только при жестких ограничениях на вид функции и закон распределения аргумента. Например, применение метода обратной функции требует вычисления на каждом участке монотонности f(x) обратной функции и производной от обратной функции.

Вычисление W(y) методом характеристической функции [КК] ограничено таким набором w(x) и f(x), для которых можно вычислить характеристическую функцию в явном виде, а по характеристической функции вычислить W(y).

В связи с этим целесообразно воспользоваться приближенным методом, сущность которого заключается в вычислении некоторых характеристик закона распределения и по ним восстановлении всего закона распределения. В качестве таких характеристик можно взять начальные моменты закона распределения:


m_k(h)=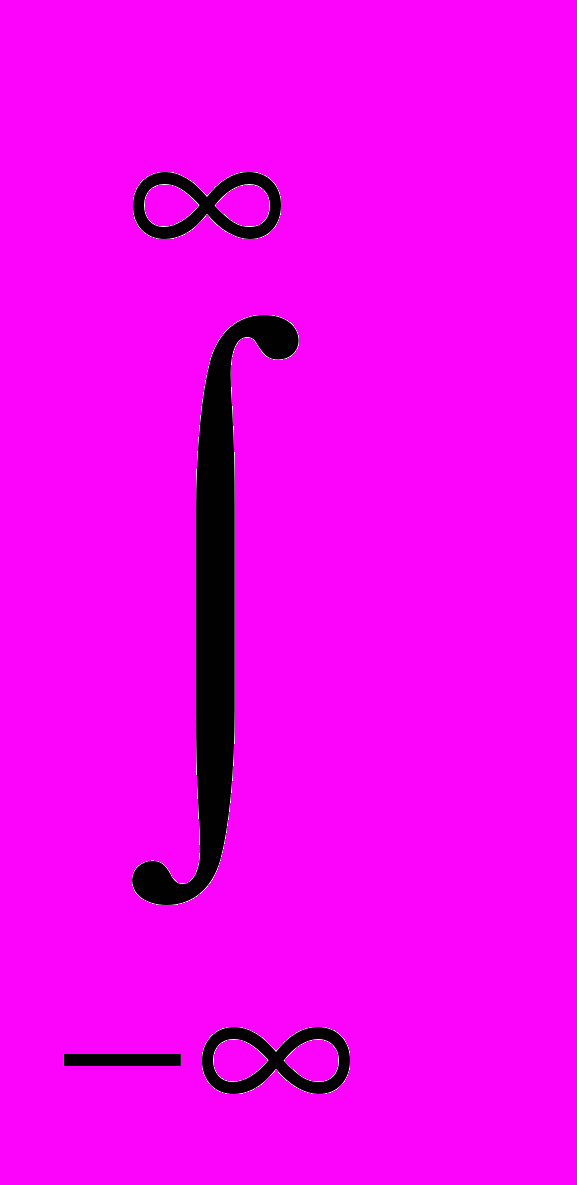...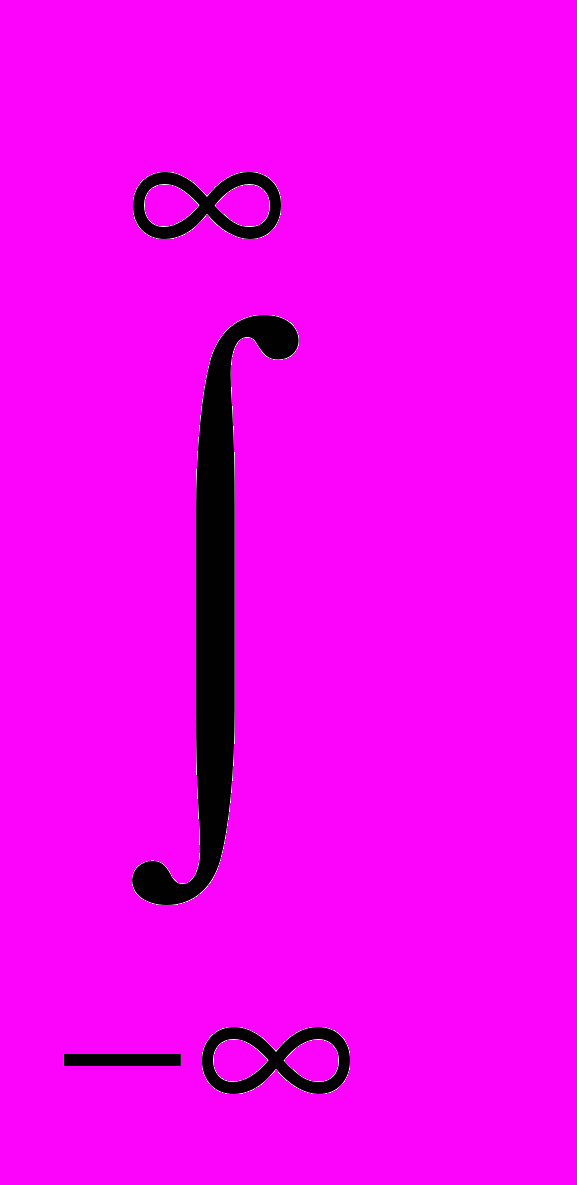f(x₁,...,x_n)^kw(x₁,...,x_n) dx₁...dx_n

или для одномерного случая h=f(x)

m_k(h)=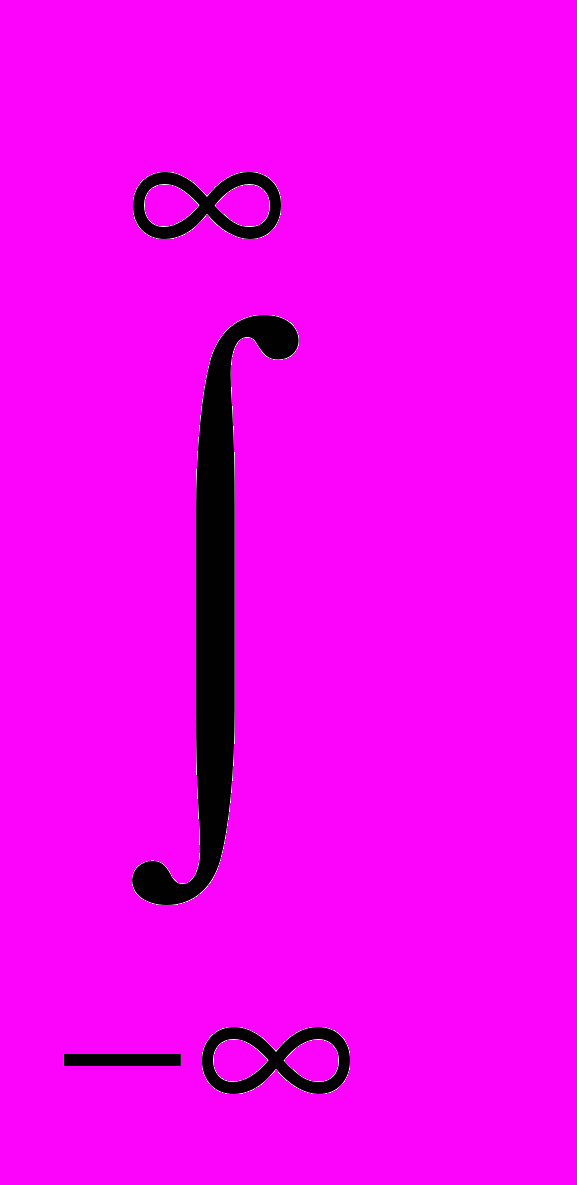f(x)^kw(x) dx

при условии, что этот интеграл сходится абсолютно [КК].

Поскольку данный методический подход возможен практически для любых вычислительных алгоритмов, то для иллюстрации его реализуемости можно ограничиться классом функций, представимых конечным степенным рядом. В этом случае если f(x)= 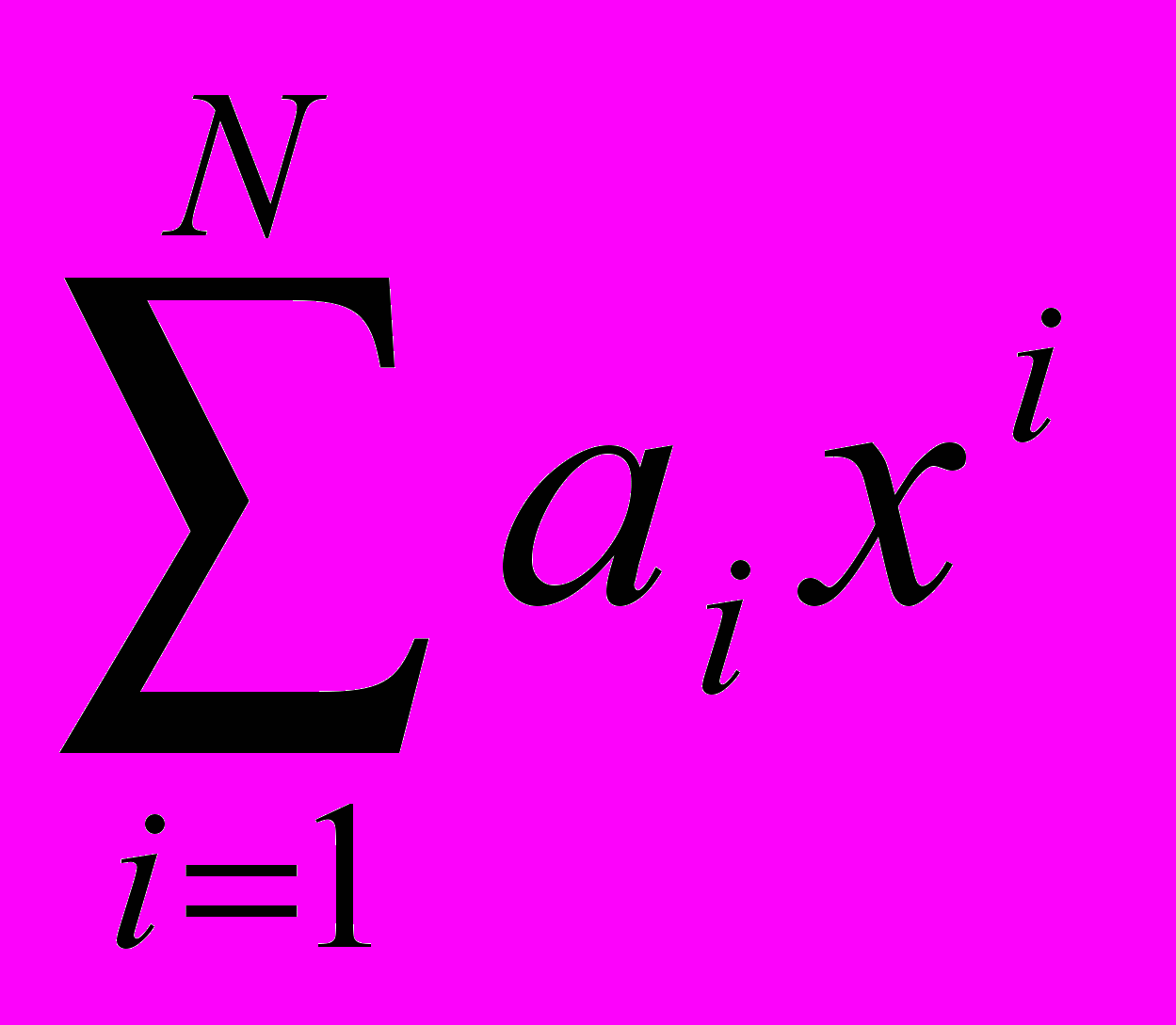(общий вид), то определение первых t=r/N моментов случайных величин h=f(k) выполняется по следующему алгоритму (r – число первых начальных моментов закона распределения w(x), принимающих значения m₁(),...,m_r()).


Алгоритм A

А₁. i:=1.

А₂. Вычислить значения b_j, j=1,...,N полинома f(x)ⁱ путем перемножения f(x)ⁱ и f(x)^i-1: если f(x)= 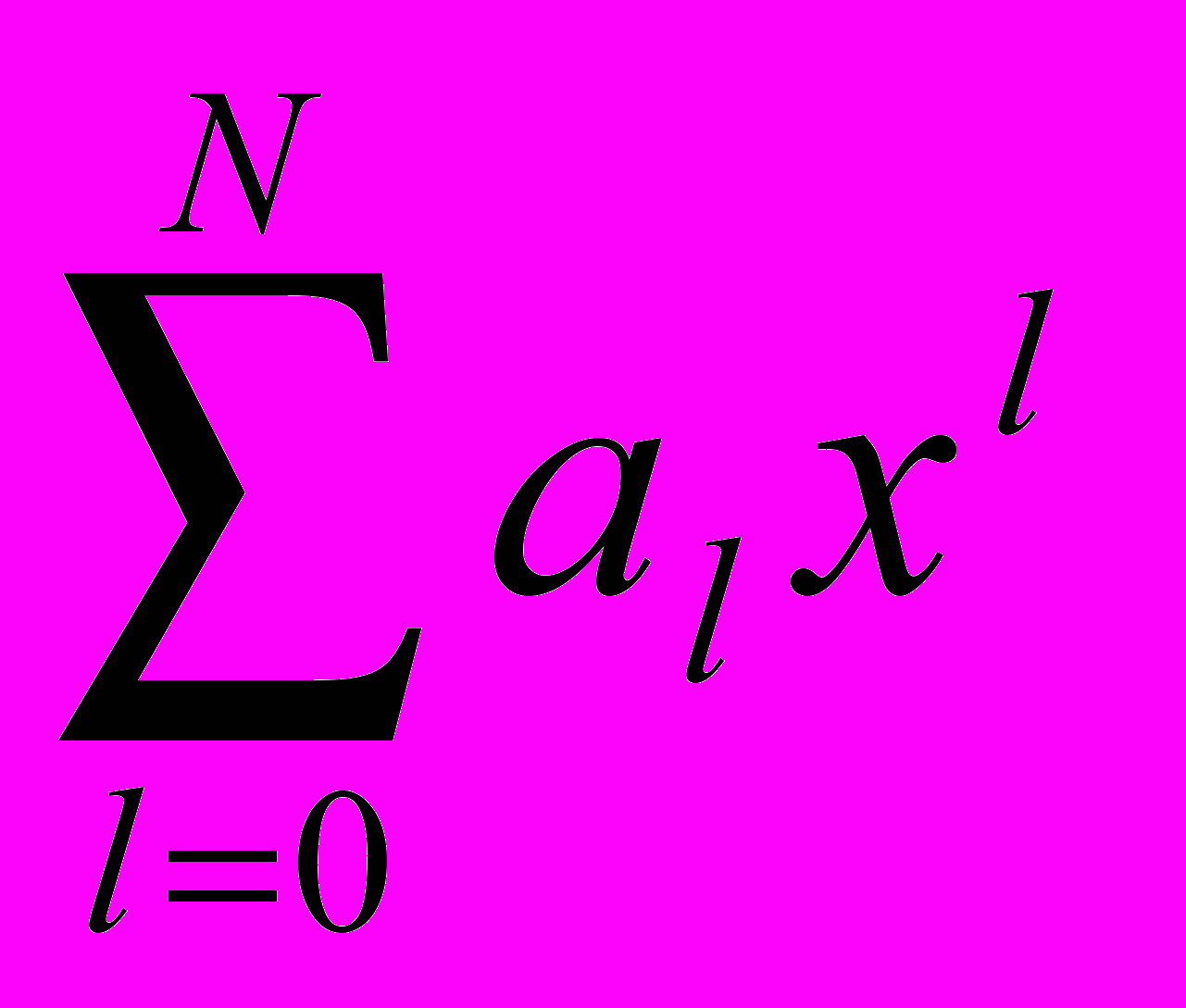и f(x)^i-1=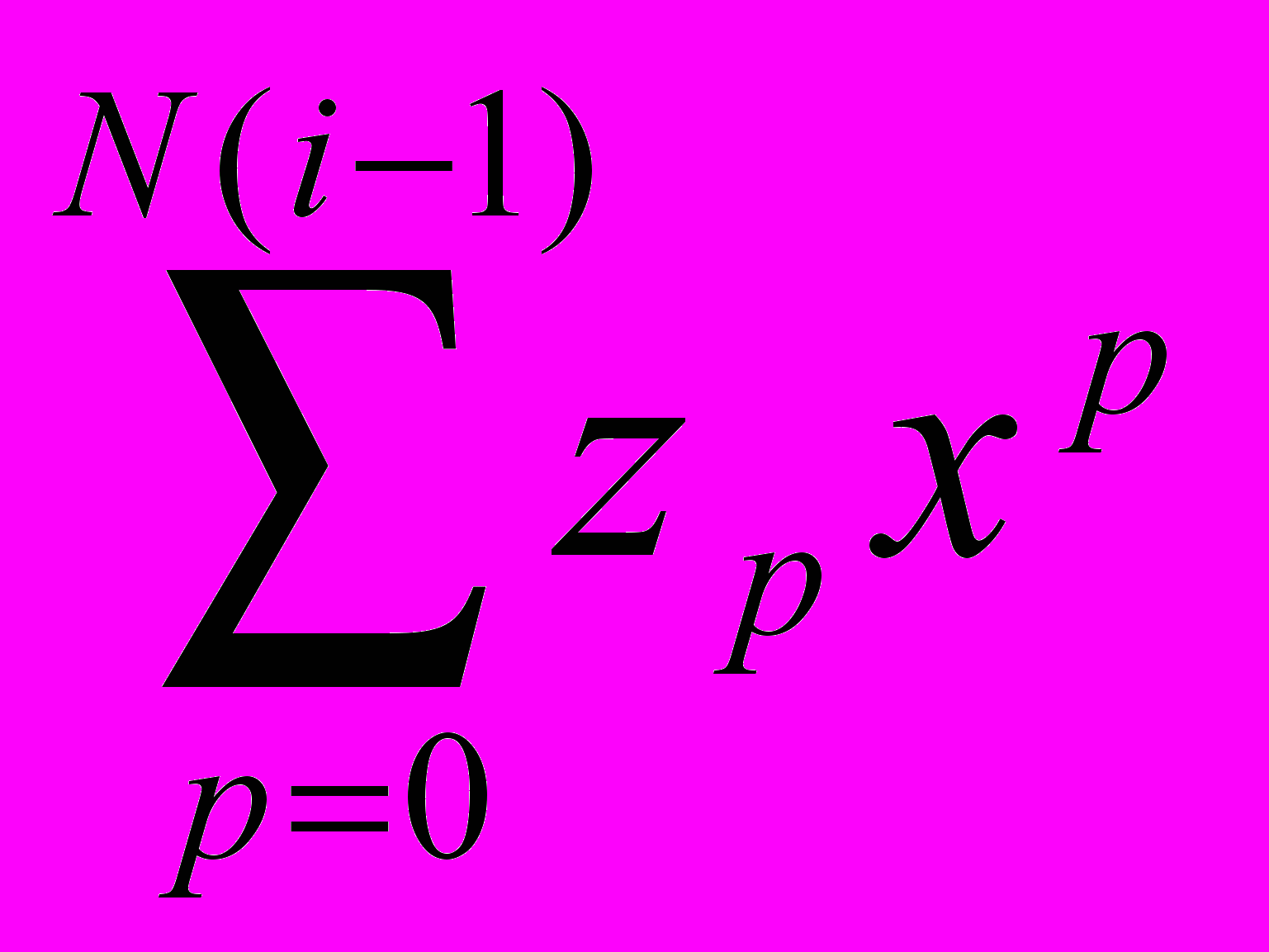, то b_j=.

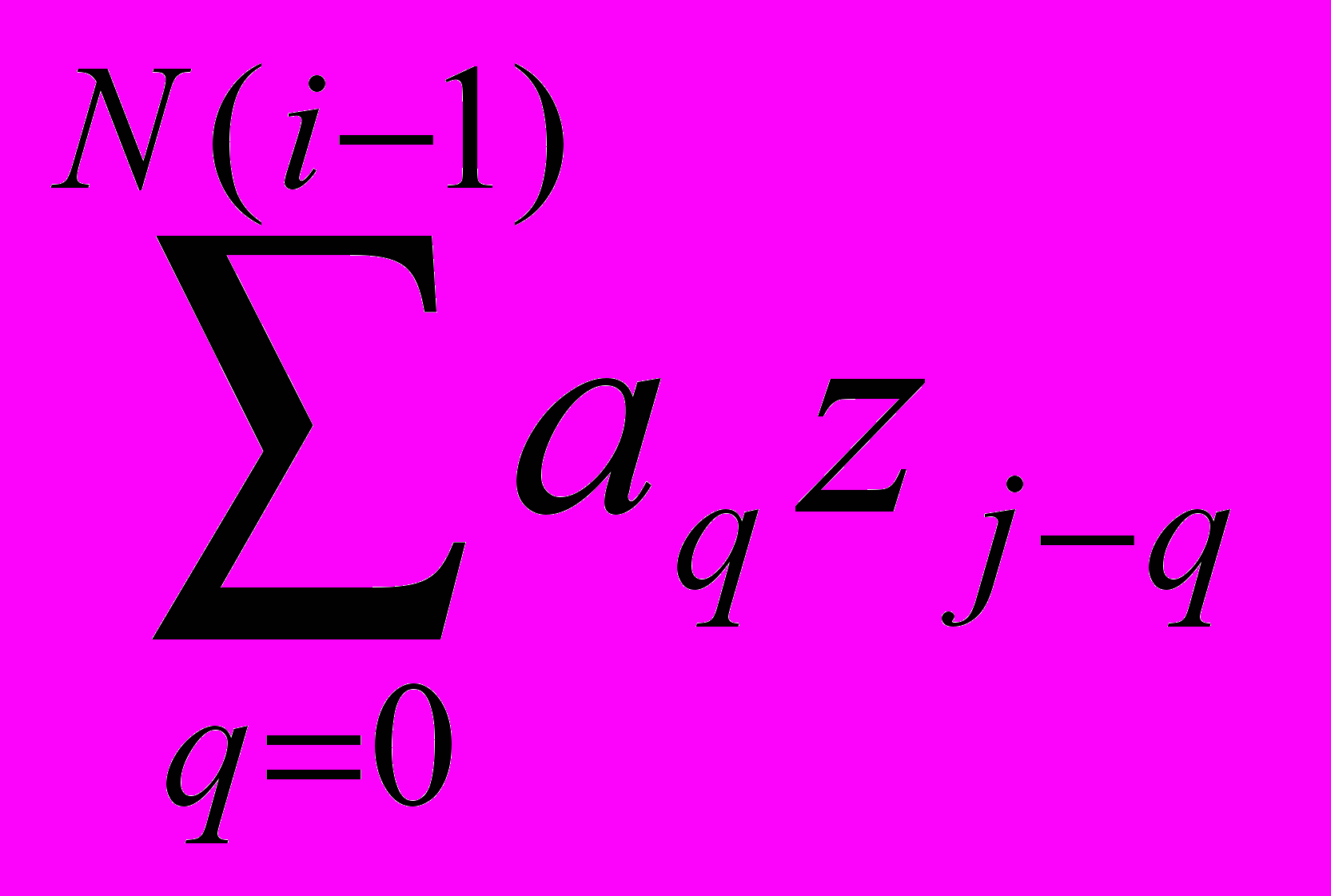А₃. Вычислить m_i(h)=.

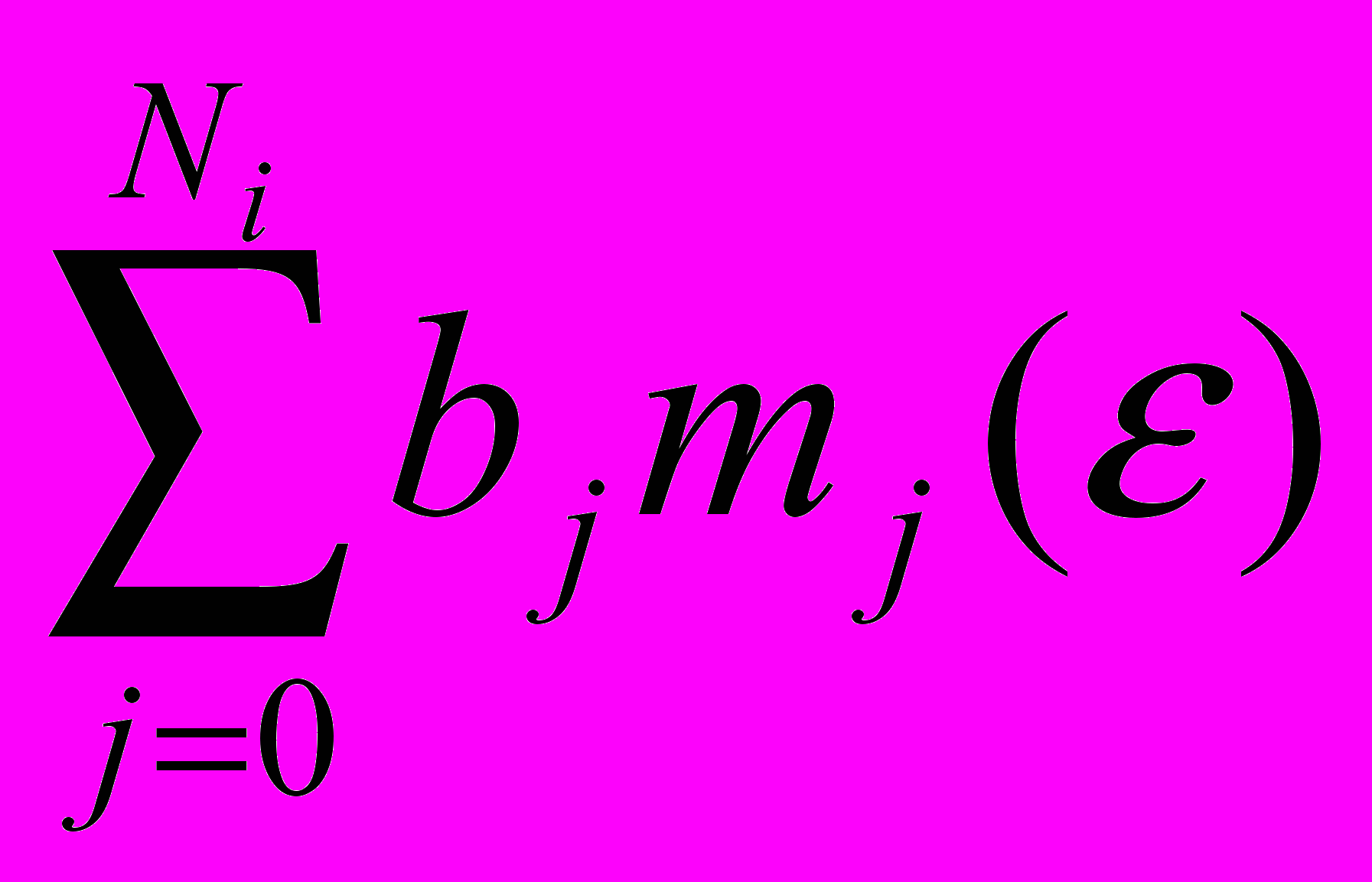А₄. i:=i+1.

А₅. Если ir/N, то переход на п.А₂. В противном случае алгоритм завершается.


Кроме рассмотренного, возможно применение алгоритмов реализующих методы вычисления моментов функции от случайных величин с использованием моментопроизводящих или кумулянтных функций [КК].

Задача вычисления закона распределения F(y) в заданной точке y₀ по L моментам формулируется следующим образом.

Дано: m_i, i=1,...,L - начальные моменты F(y).

Необходимо: определить значения sup F(y₀) и inf F(y₀).

Метод вычисления sup F(y₀) и inf F(y₀) по известным начальным моментам F(y) описан в [Че]. Алгоритм вычисления sup F(y₀) и inf F(y₀) для L=2k-1, k=1,2..., и известных а и b – конечных значений y, меньше и больше которых соответственно значения функции принимать не могут, реализуют данный метод с некоторыми модификациями.


Алгоритм Б

Б₁. Сформировать ряд «подходящих» дробей к интегралу

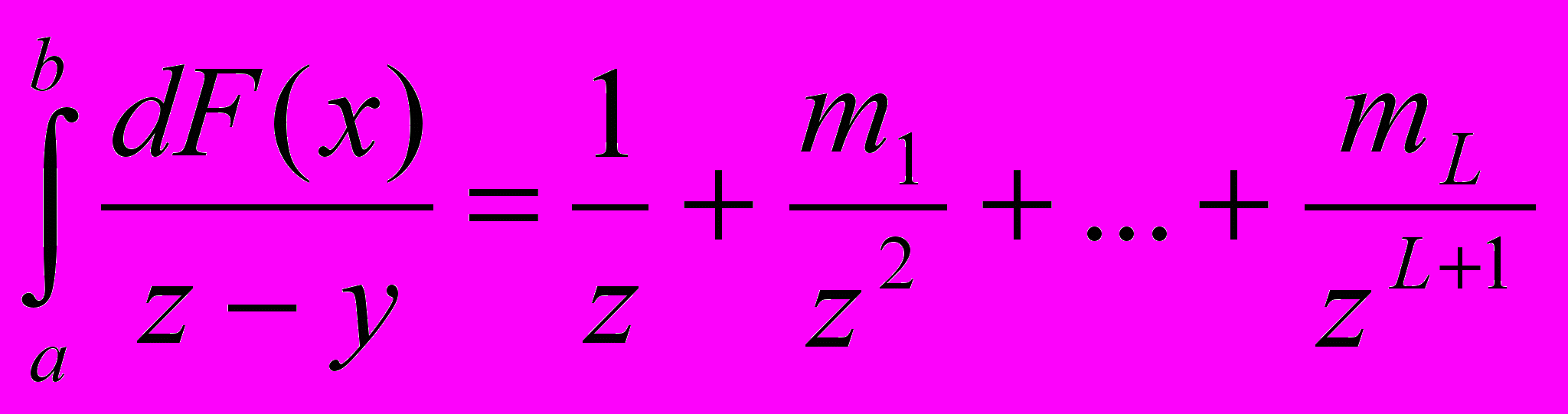
Б₂. Преобразовать «подходящую дробь» в непрерывную вида

.

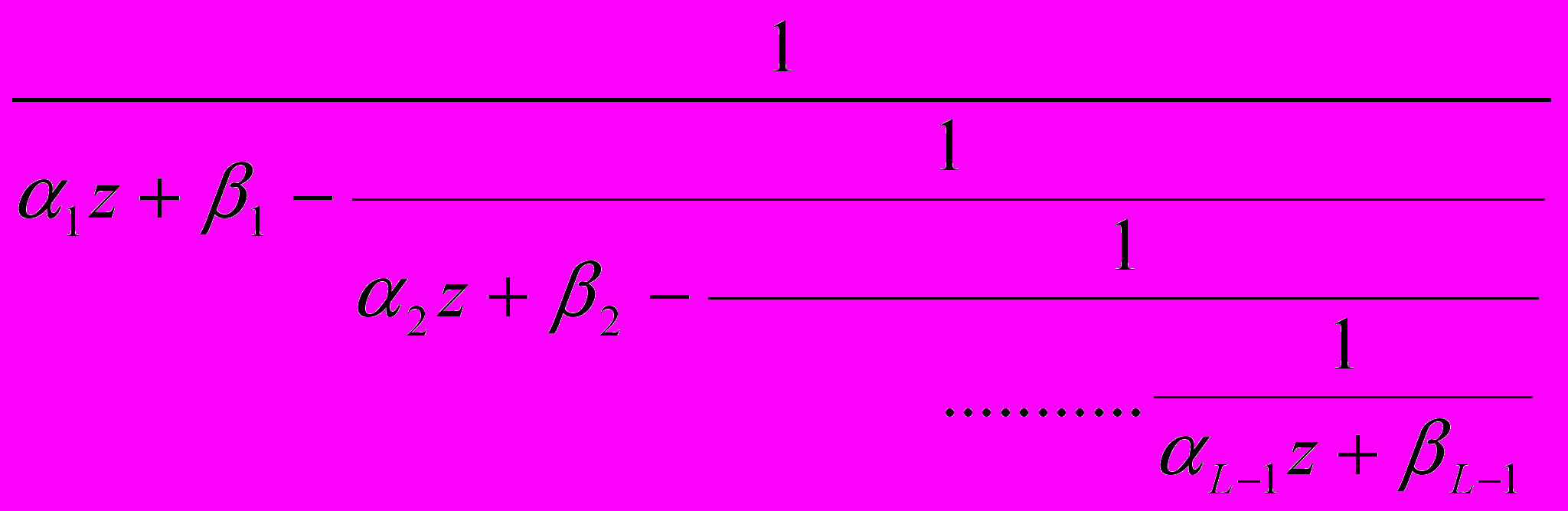Б₃. Привести непрерывную дробь к дробно рациональному виду _L(z)/_L(z).

Б₄. Выполнить пункты Б₂ и Б₃ для L=L-1 и вычислить
_L-1(z)/_L-1(z).

Б₅. Определить функцию .

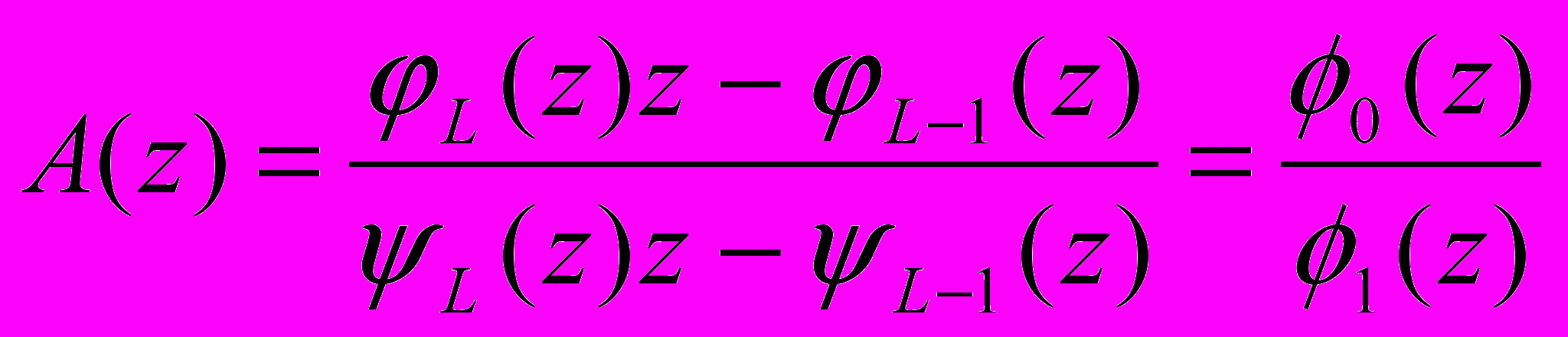Б₆.Определить вещественные корни полинома ₁(z).

Б₇. Вычисление интеграла 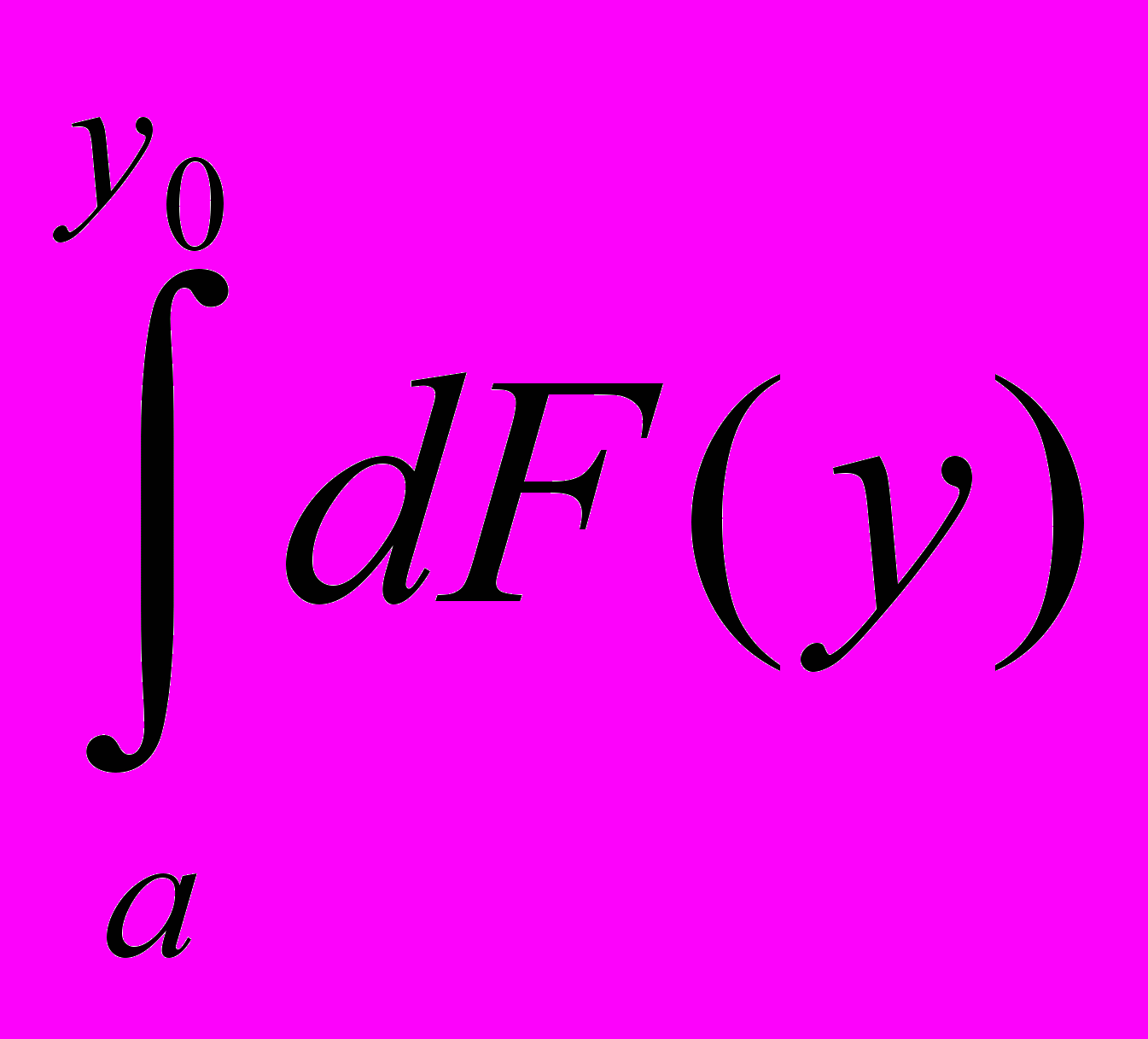с помощью вычетов. При этом inf F(y₀) будет равно сумме вычетов ₀(z)/₁(z) для всех y,y₀, а sup F(y₀), будет равно сумме inf F(y₀) и очередного вычета. Среднее значение F_ср(y₀)=(sup F(y₀)+inf F(y₀))/2 и значение =(sup F(y₀)+inf F(y₀))/2, определяющее точность восстановления функции распределения, зависят от m_i, i=1,...,L и y₀. Однако 1/L+1.


Таким образом, с помощью алгоритмов А и Б можно с заданной точностью рассчитать вероятностные характеристики исследуемой программы.

7.6.4.Обоснование критериев принятия решения
о наличии в программе РПС

Задача выбора критериев наличия в исследуемой программе РПС в общем виде, формулируется следующим образом.


Дано:

• множество G_i вероятностных характеристик случайных величин, снимаемых с заданного множества контрольных точек;
  
• эталонные значения этих ВХ G_i^* и их значения, полученные в результате n испытаний (прогонов) программы.
  

Необходимо: определить множество L_i таких, что если существует i(G_i-G_i^*>L_i), то делается вывод о наличии в исследуемой программе РПС с вероятностью Р₀.

Если в качестве информативной характеристики программы выбраны значения закона распределения выходной величины в точке y₀, то задача определения решающих правил о наличии программных закладок может быть уточнена и записана в следующем виде.

Дано: Р=F(y₀); q=1-P=P(y>y₀); задано число прогонов программы n и значения доверительной вероятности Р₀.

Необходимо: определить значение доверительного интервала L частоты появления события {A-y_j<y₀}, где y_j - j-е значение выходной величины.

Для независимых испытаний частота появления события А-y_i<y₀ является случайной величиной, распределенной по биномиальному закону с математическим ожиданием Р и дисперсией D=Pq/n. Вероятность появления k событий при n испытаниях в этом случае рассчитывается по формуле Pk=C_n^kP^kq^n-k.

В качестве доверительного интервала [P₁^*,Р₂^*] целесообразно выбирать наименьший интервал, вероятность попадания за границы которого больше (1-Р)/2. Границы доверительных интервалов для различных значений Р, Р₀ и n сведены в таблицы [Ве], что существенно облегчает задачу инженерного анализа результатов тестирования при контроле технологической безопасности программного обеспечения. С увеличением n биномиальное распределение будет стремиться к нормальному с теми же математическим ожиданием и дисперсией. При этом для вероятностного тестирования необходимо выбрать такие значения y₀, чтобы Р0,5, что позволяет заменять биномиальное распределение нормальным с максимальной точностью. Доверительный интервал в этом случае определяется по формулам P(P-P^*<L_экс)=P₀, L_экс=arg Z^*((1+P₀)/2), где arg Z^* - функция, обратная нормальной функции распределения Z^*, полученная по таблицам.

С учетом того, что значение F(y₀) вычисляется с точностью , доверительный интервал L=L_экс+, то есть если при проведении испытаний значений Р^* будет отличаться от аналогично рассчитанного на величину, большую, чем L_экс+, то принимается решение о наличии в исследуемой программе РПС с вероятностью Р₀.

Аналогичным образом доверительный интервал может быть определен и для случая, когда в качестве информативной характеристики программы используется математическое ожидание выходной случайной величины: .

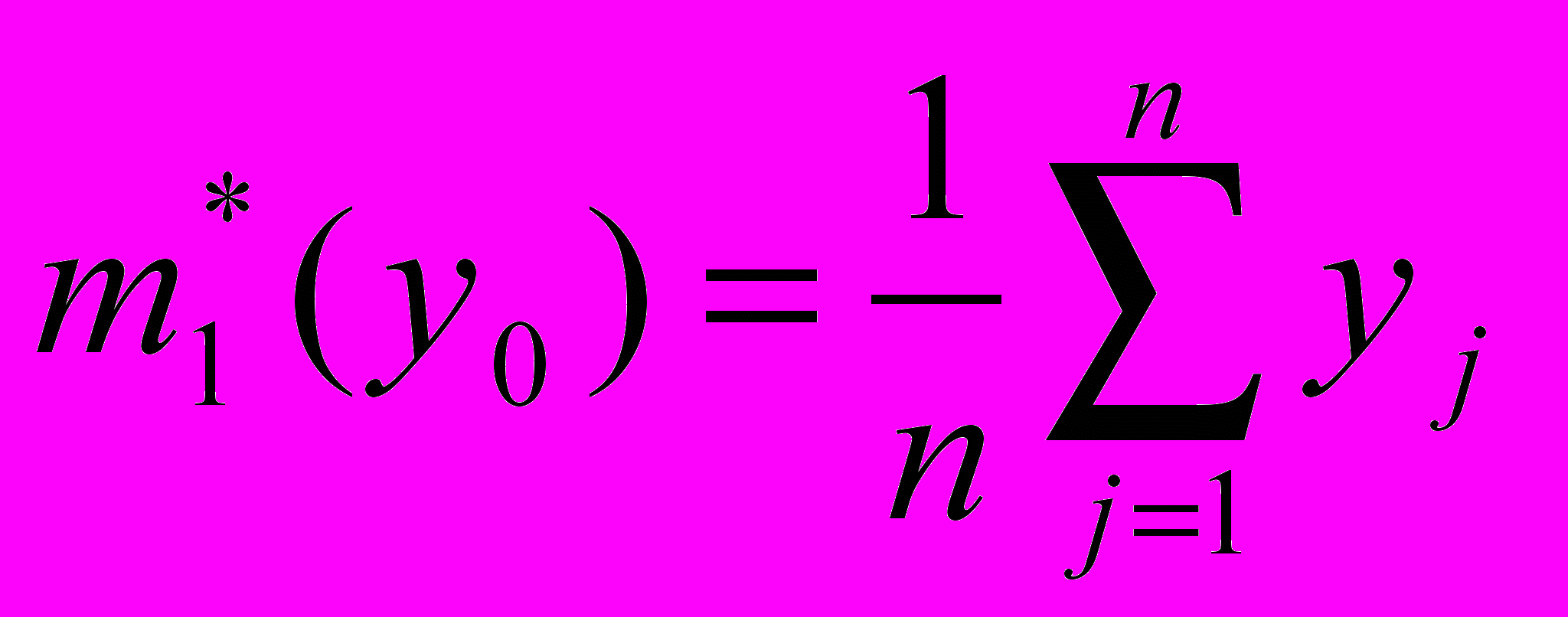Так как y_j представляет собой случайные величины с одинаковым законом распределения, то законы распределения и их суммы стремятся к нормальному с математическим ожиданием m₁(y) и дисперсией D(y)/n.

В этом случае доверительный интервал определяется по формуле L_экс=arg Z^*((1+P₀)/2), .

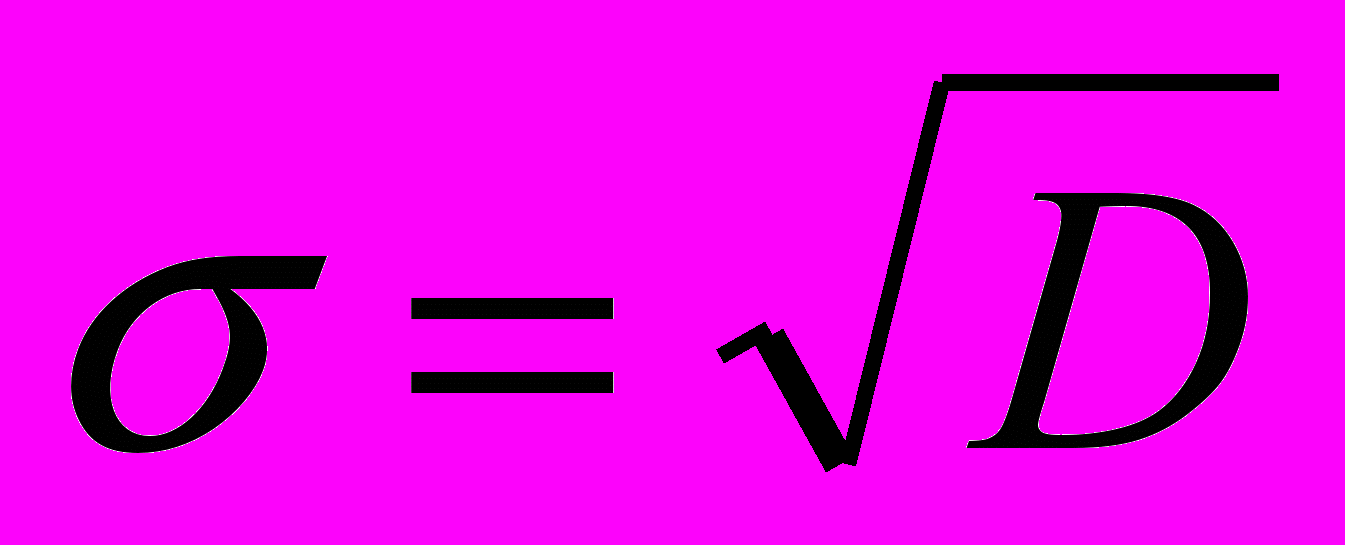Пользуясь методами математической статистики, можно аналогичным образом построить доверительные интервалы и для других ВХ. При этом факторы, влияющие на достоверность определения вероятности наличия в программном обеспечении РПС, можно разбить на три основные группы.

1.  Точность аналитического вычисления ВХ. Если в качестве метода вычислений использовать метод моментов, то ошибки будут вызваны точностью представления реализуемой функции степенным рядом и ограниченным числом начальных моментов. Если функция представляется конечным степенным рядом или ошибка разложения в ряд достаточно мала, то можно считать, что точность вычисления ВХ будет зависеть от качества моментов. При заданной допустимой ошибке  вычисления закона распределения требуемое число моментов может быть достаточно просто рассчитано.

2.  Ограниченность числа испытаний (прогонов) программы. При известных значениях доверительного интервала с помощью методов статистики можно определить необходимое число испытаний, обеспечивающее достоверность результата не меньше Р₀.

3.  Закон распределения входных случайных величин. Для заданного закона распределения аргумента w(x) функции f₁(x) и f₂(x) будут неразличимы, если для каждой точки y

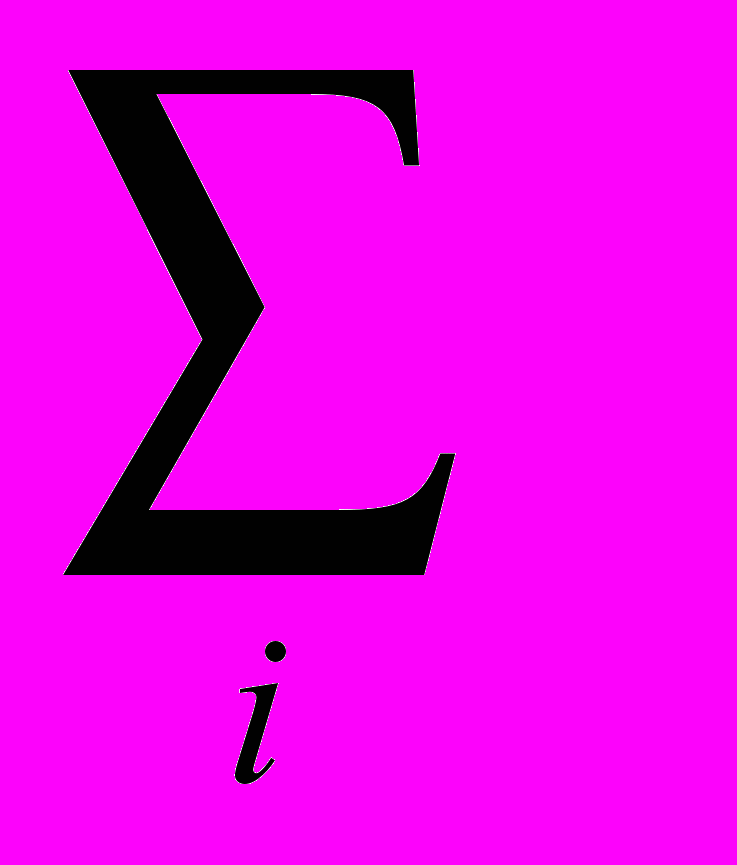
F(y)=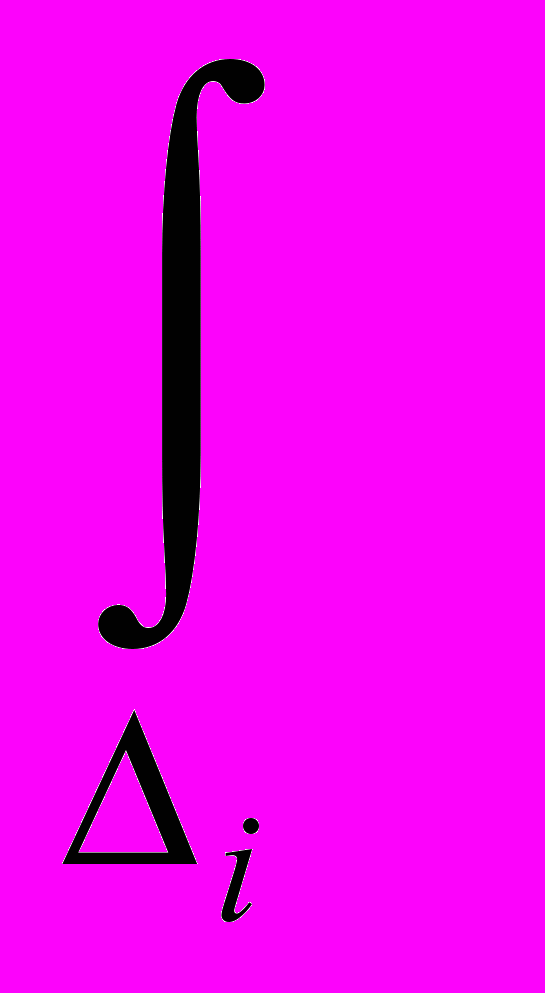w(x) dx=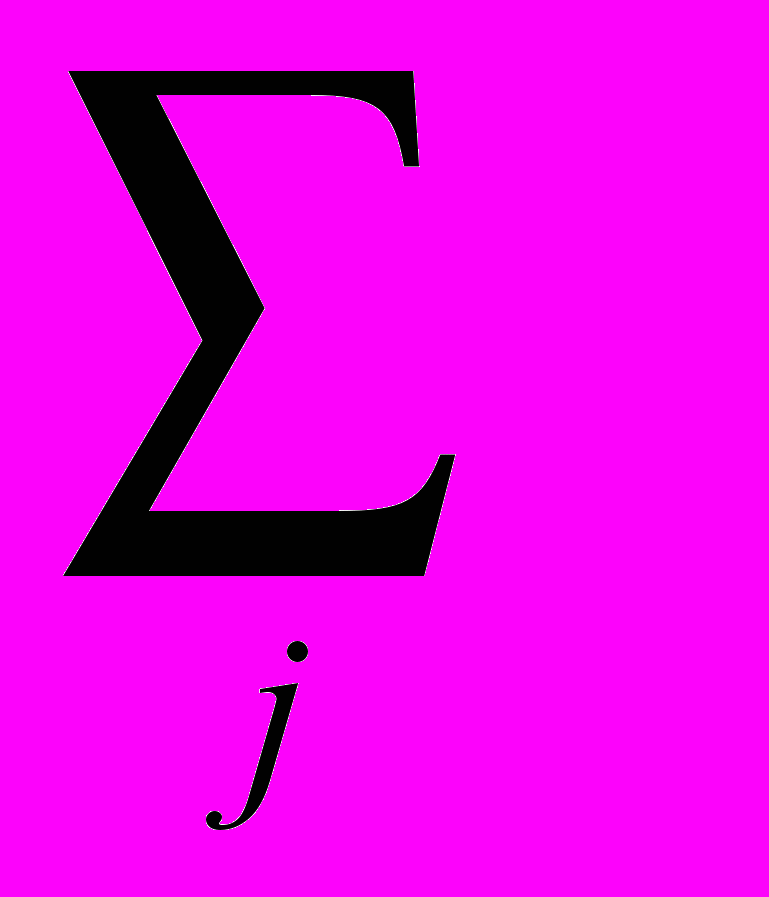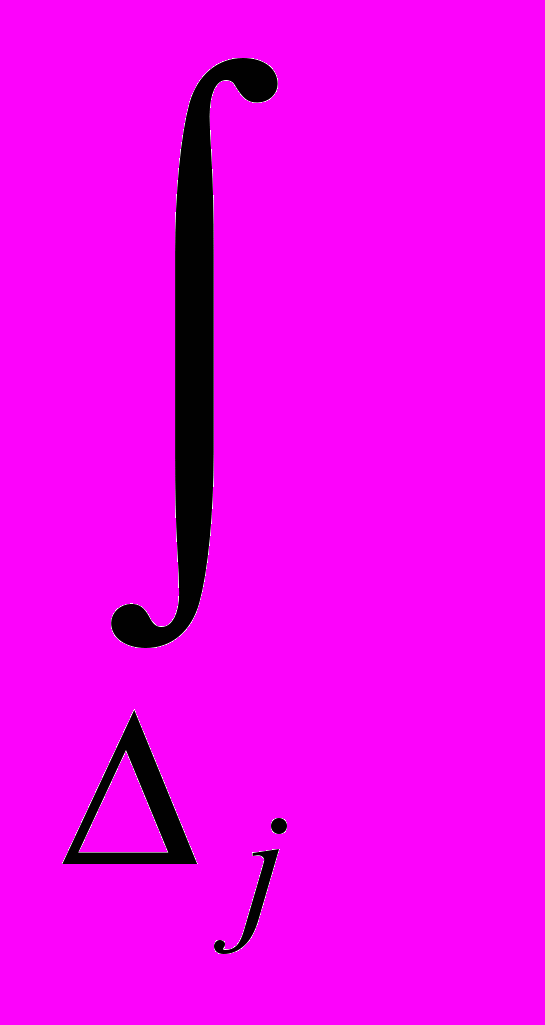w(x) dx

или если задаться допустимой точностью вычисления  функции распределения:

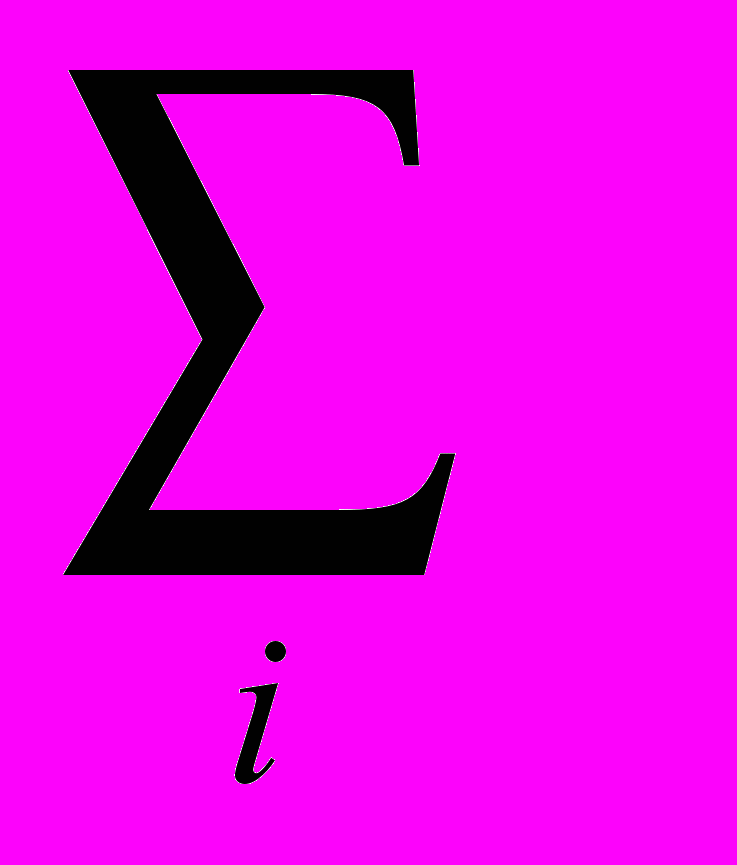
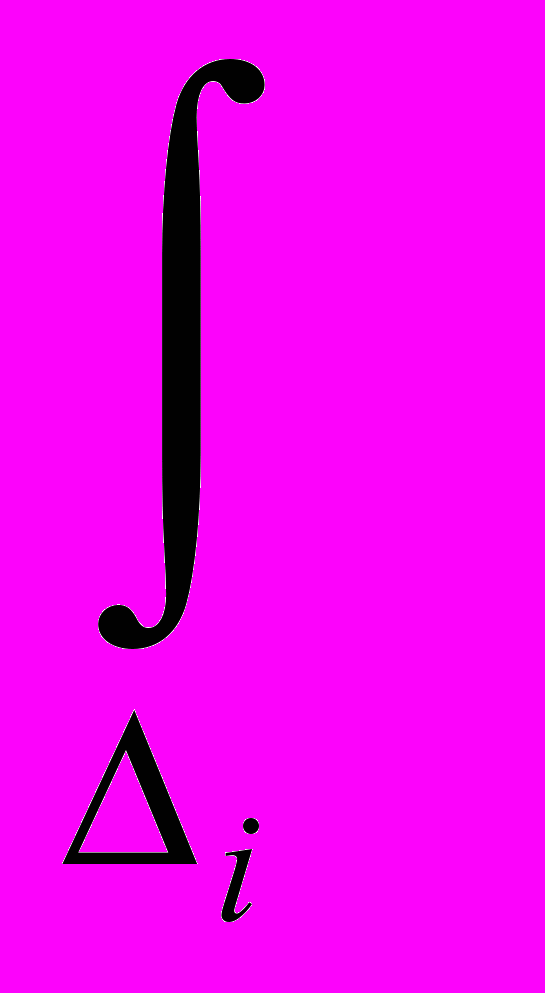w(x) dx-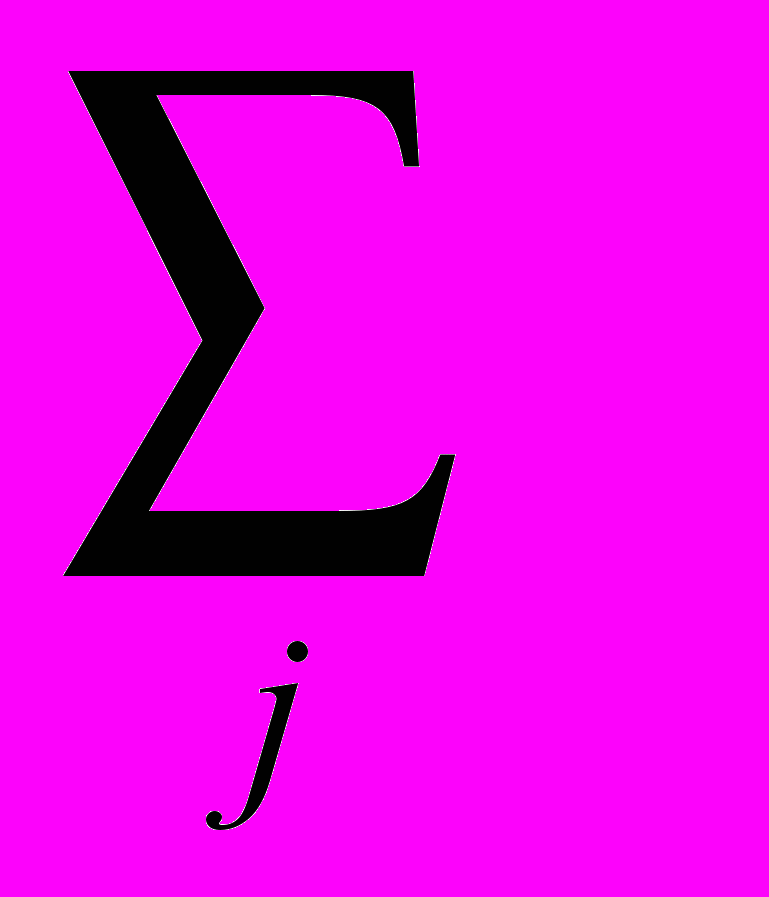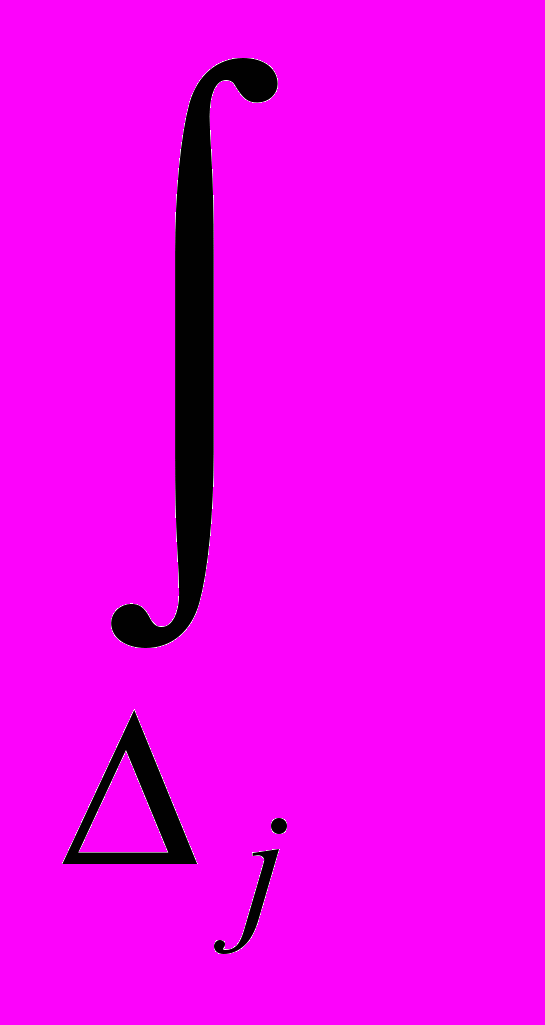w(x) dx,

где _i - интервалы аргумента, где f₁(x)<y;

_j - интервалы аргумента, где f₂(x)<y.

Проверяя функции при различных законах распределения аргумента, можно сократить множество неразличимых функций. Для каждого класса допустимых функций можно найти такой набор законов распределения аргументов, который обеспечивает минимизацию области неразличимых функций.