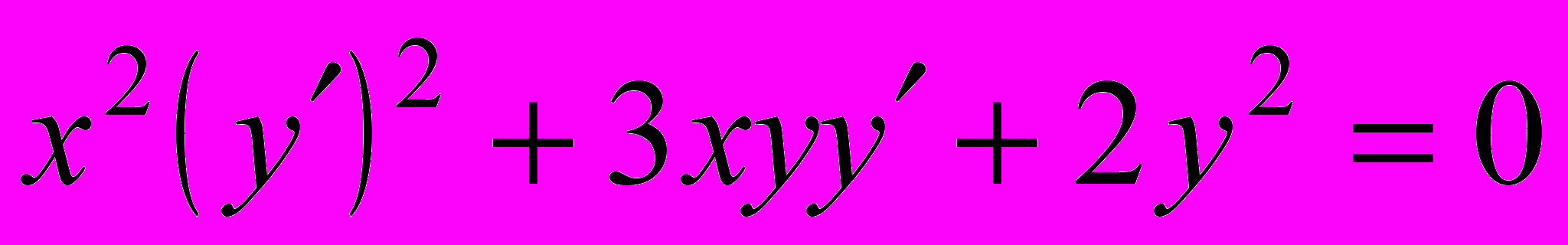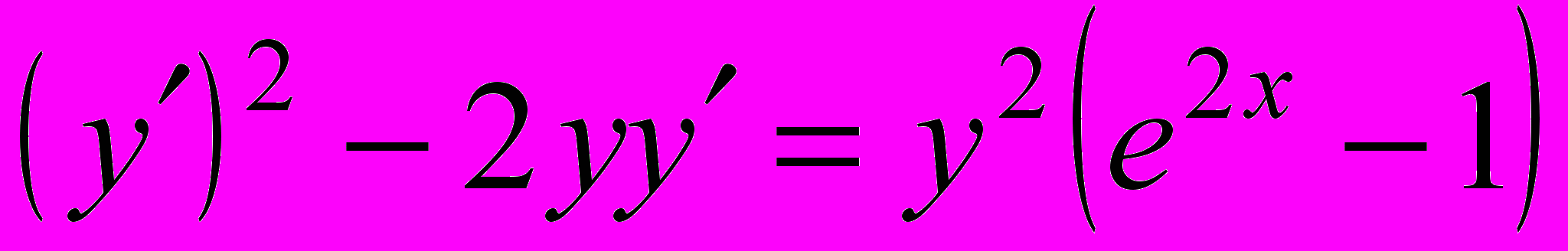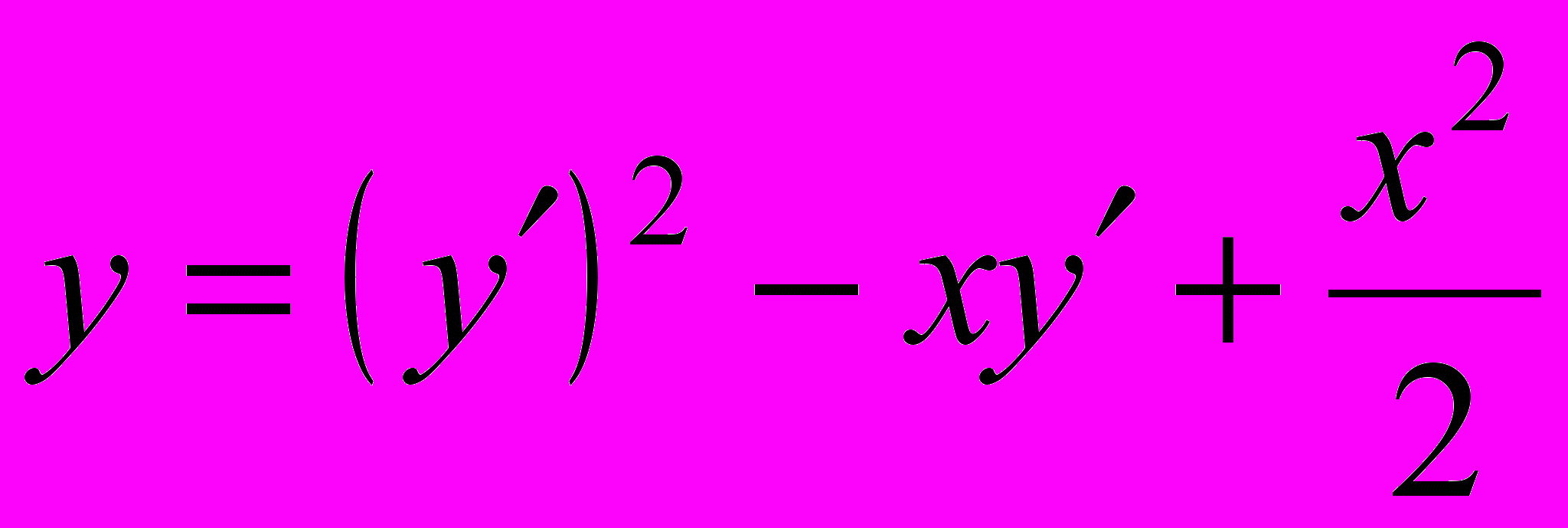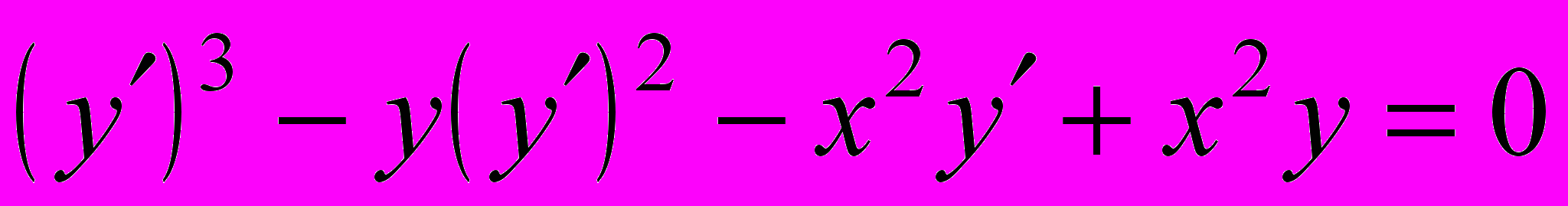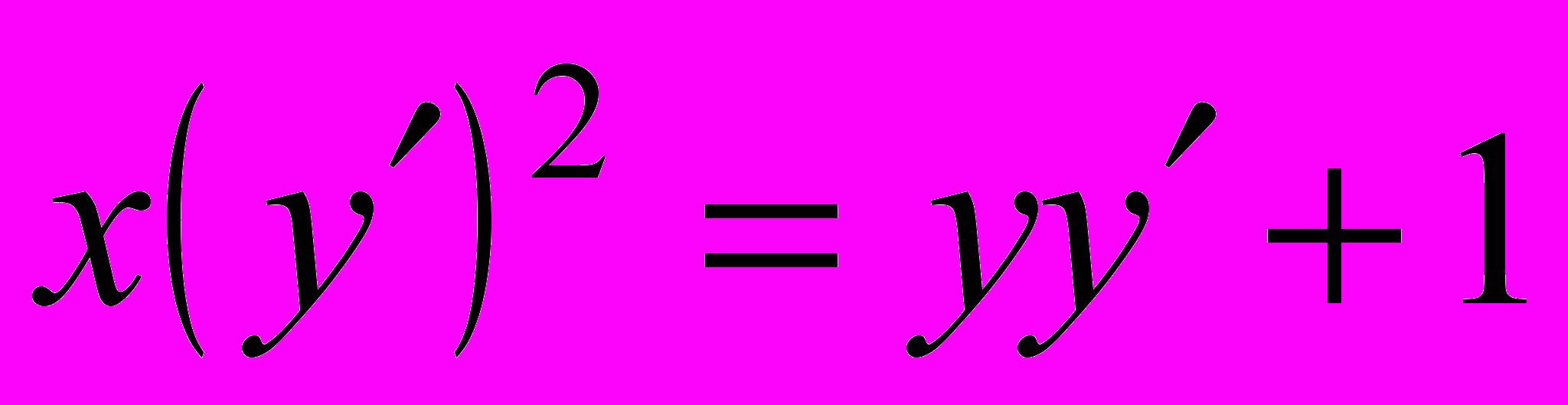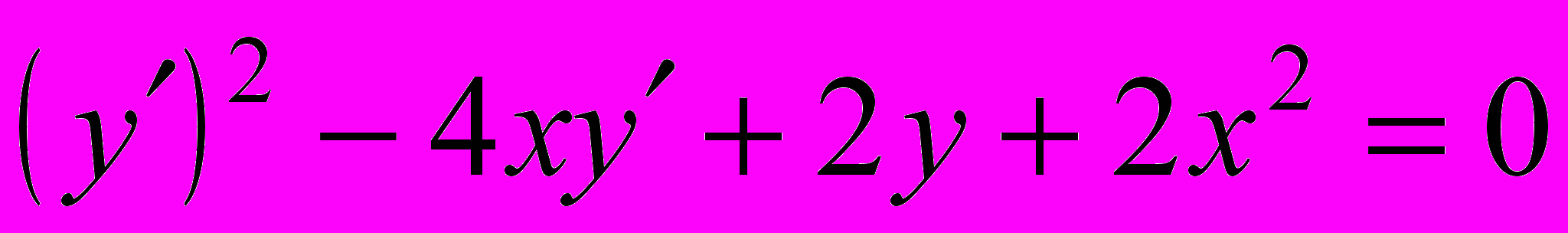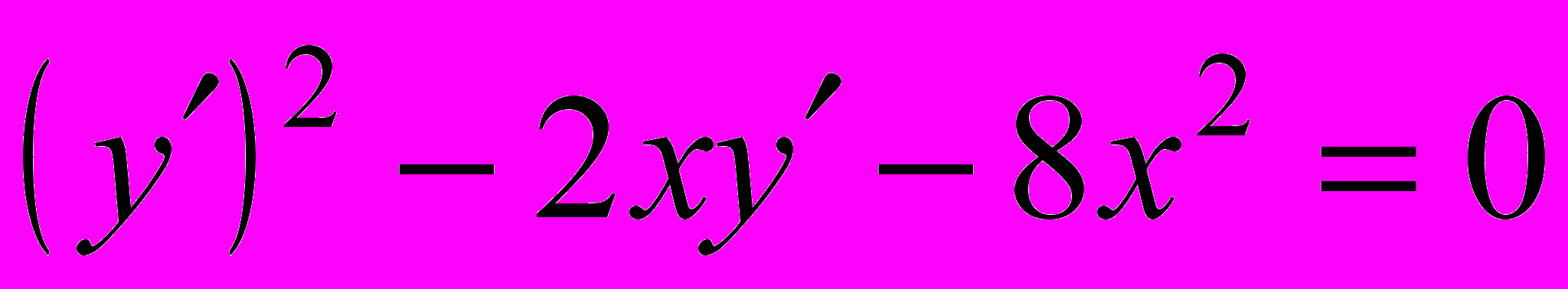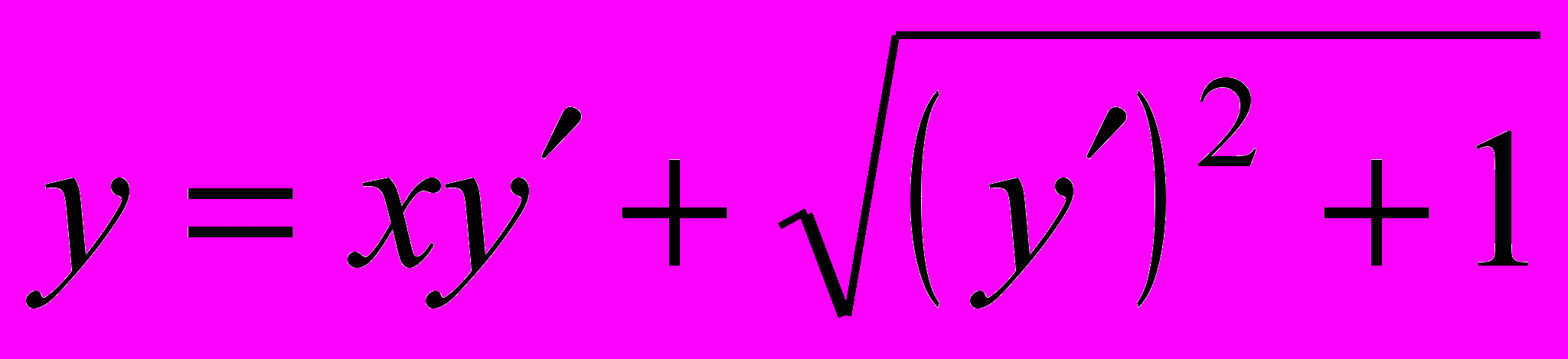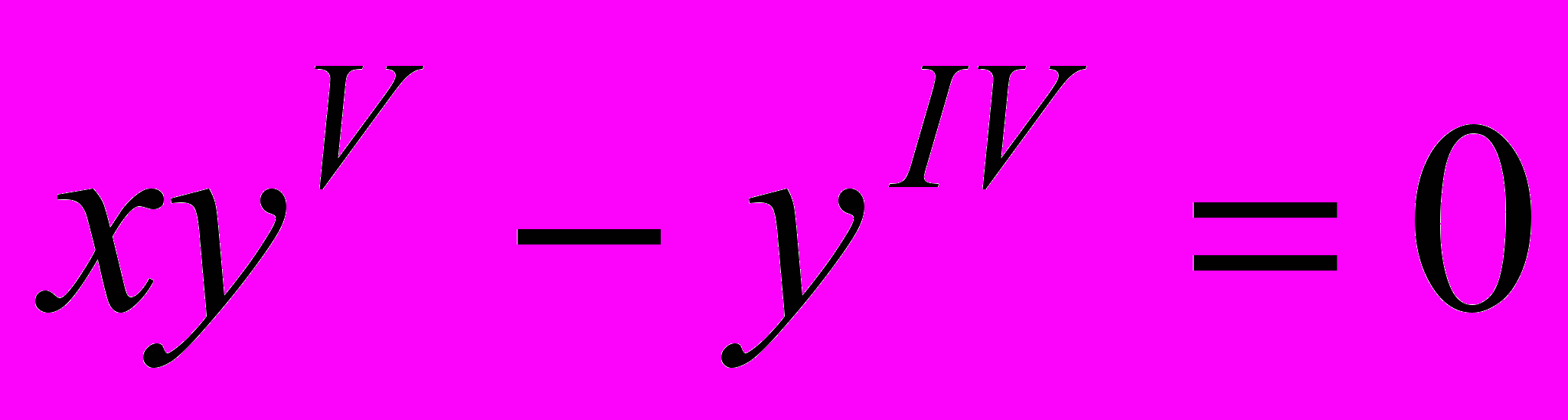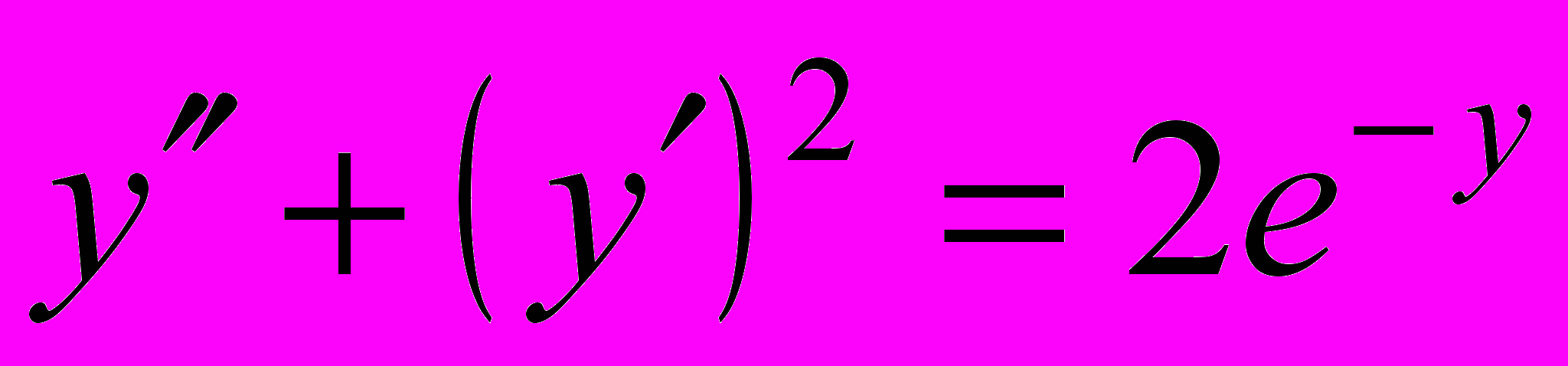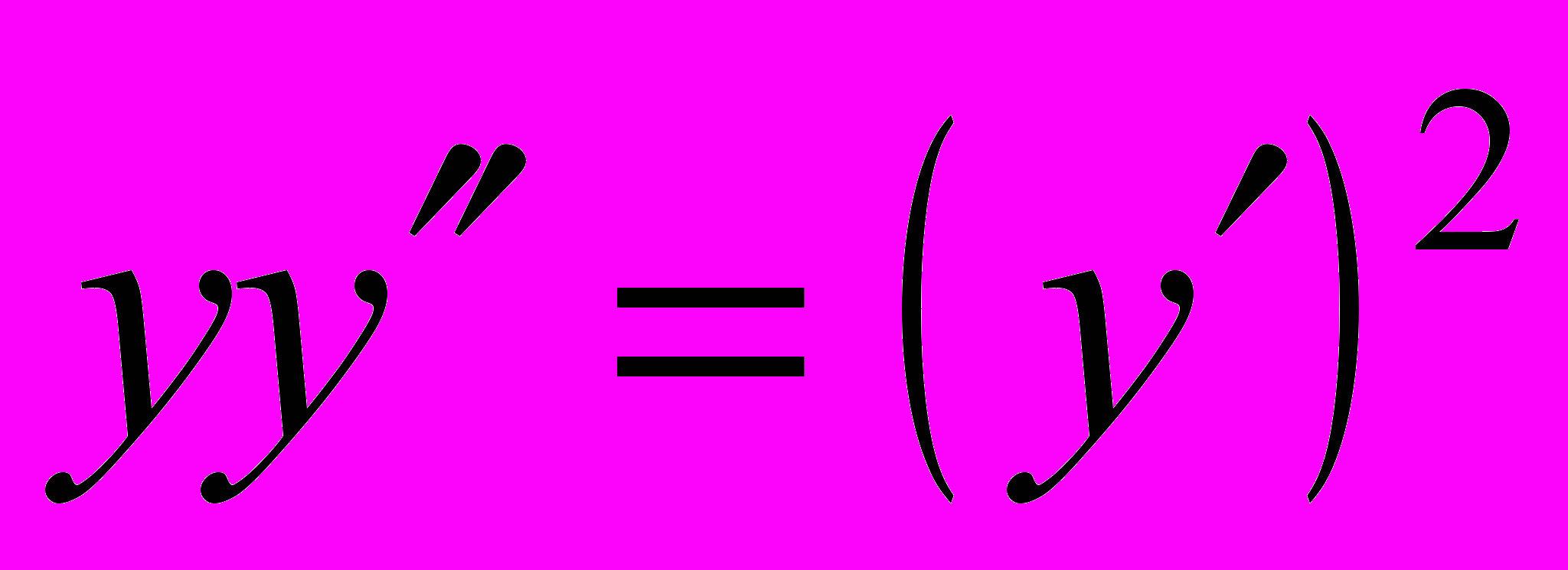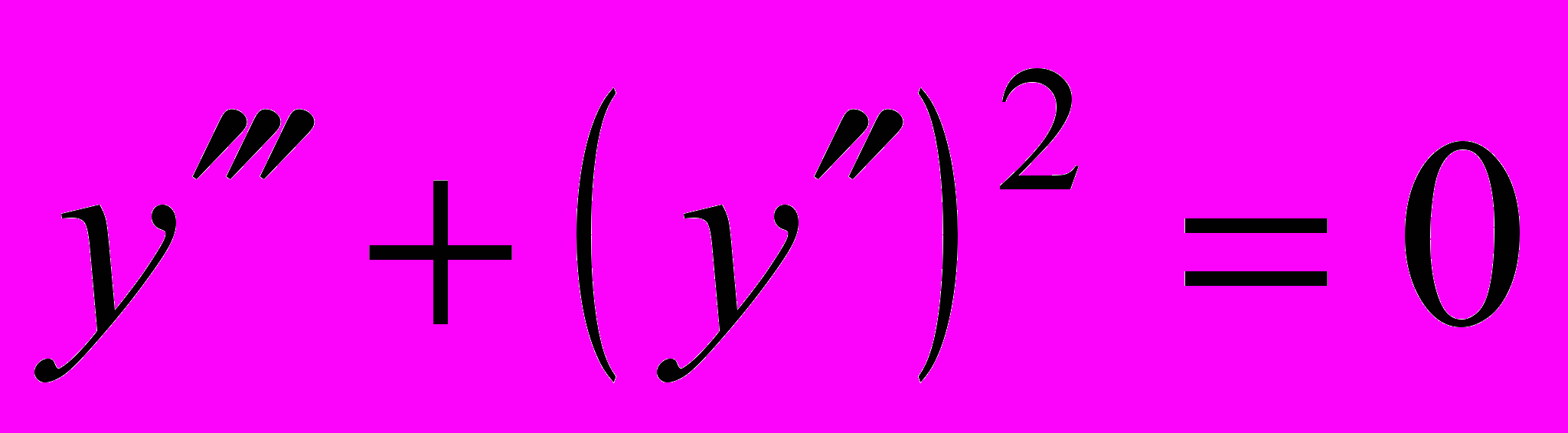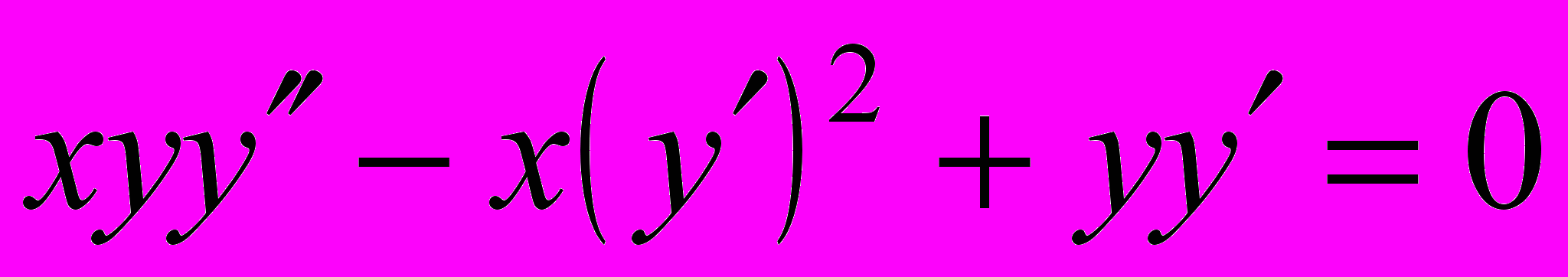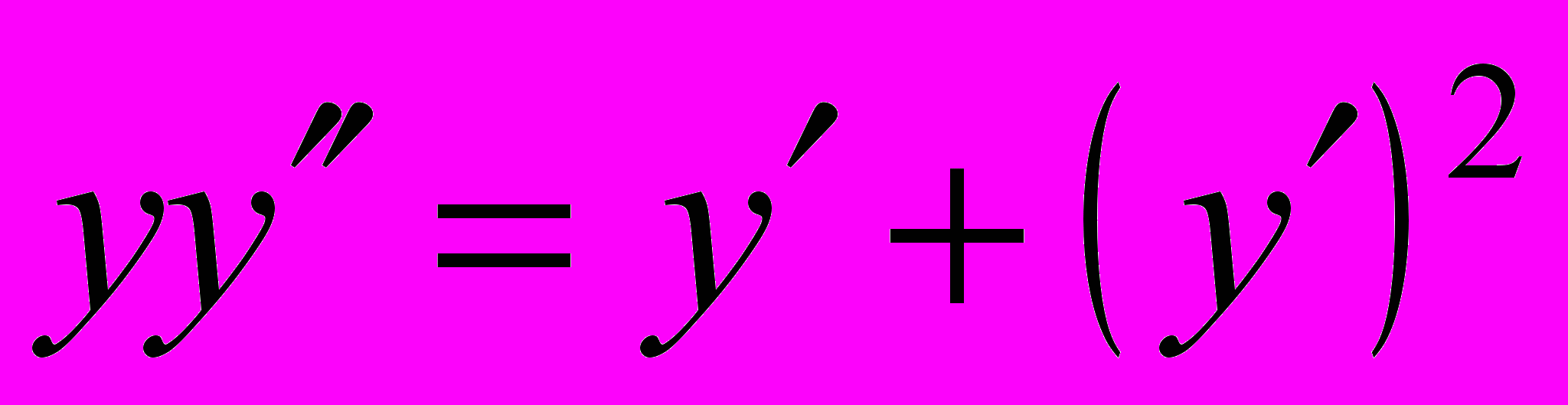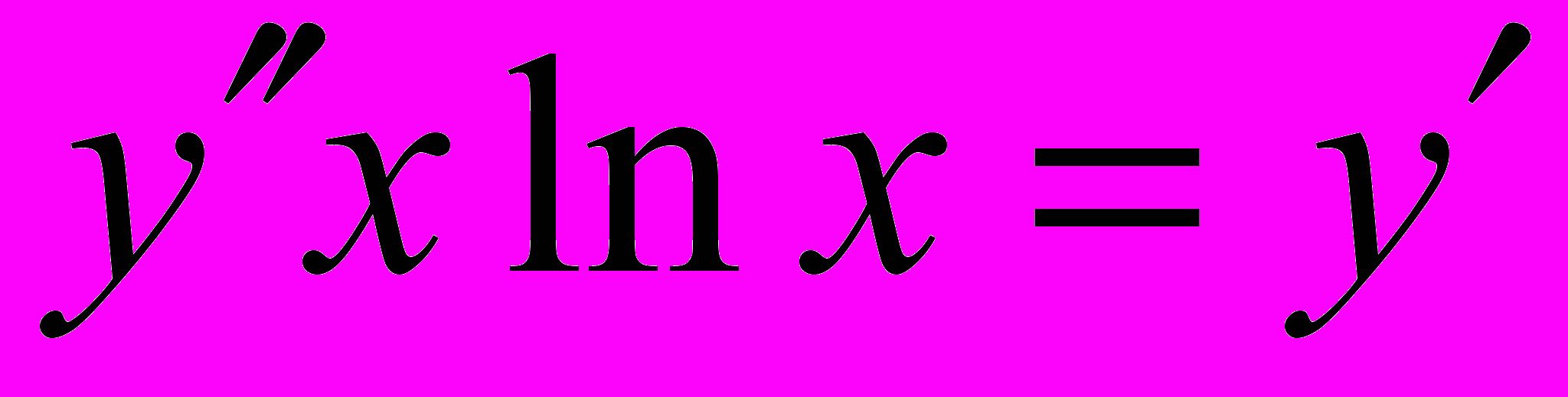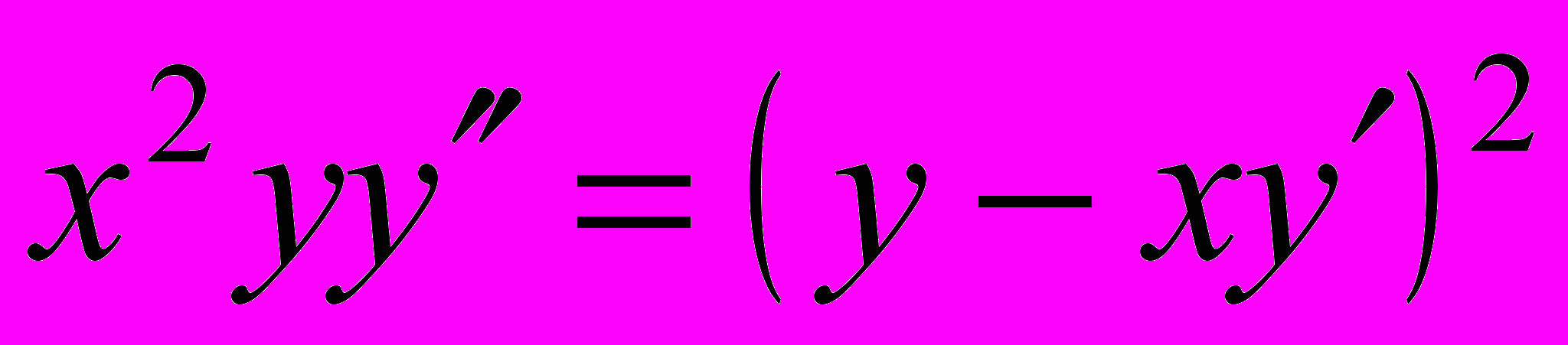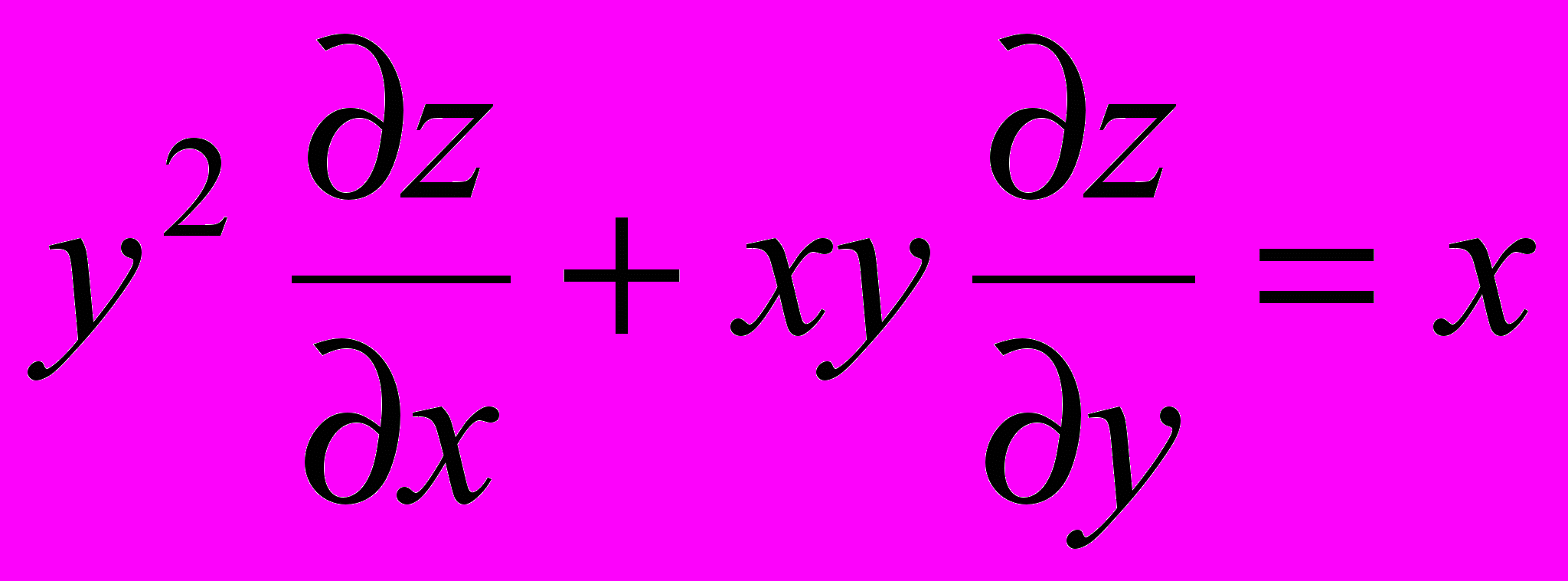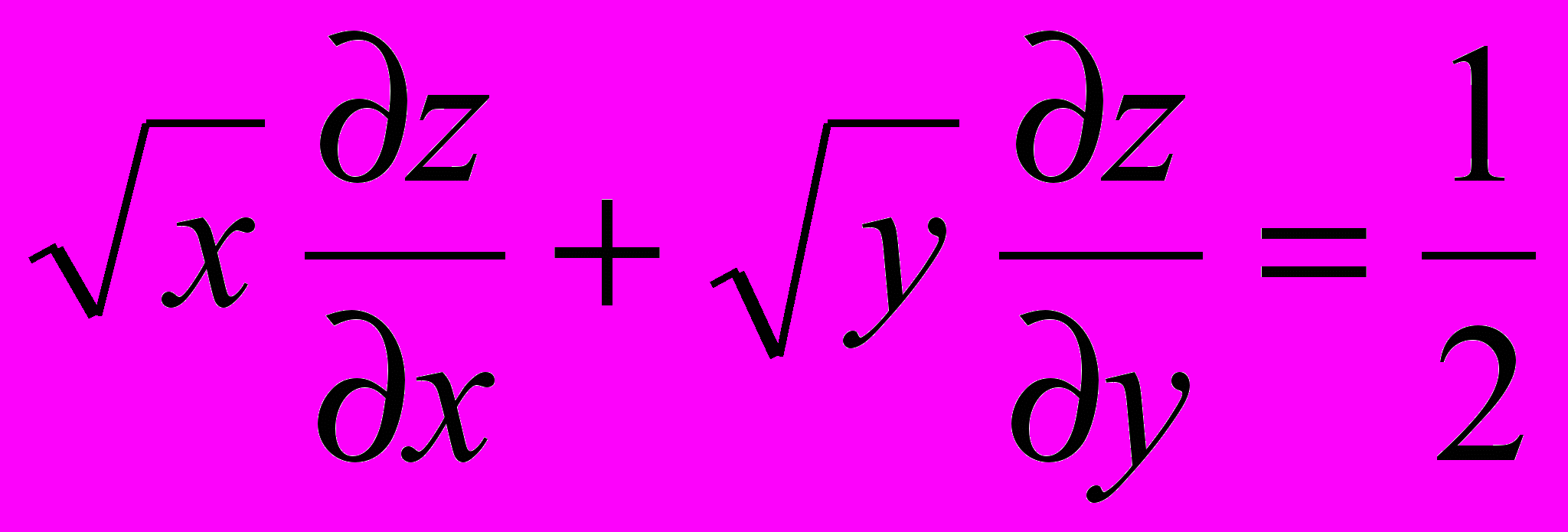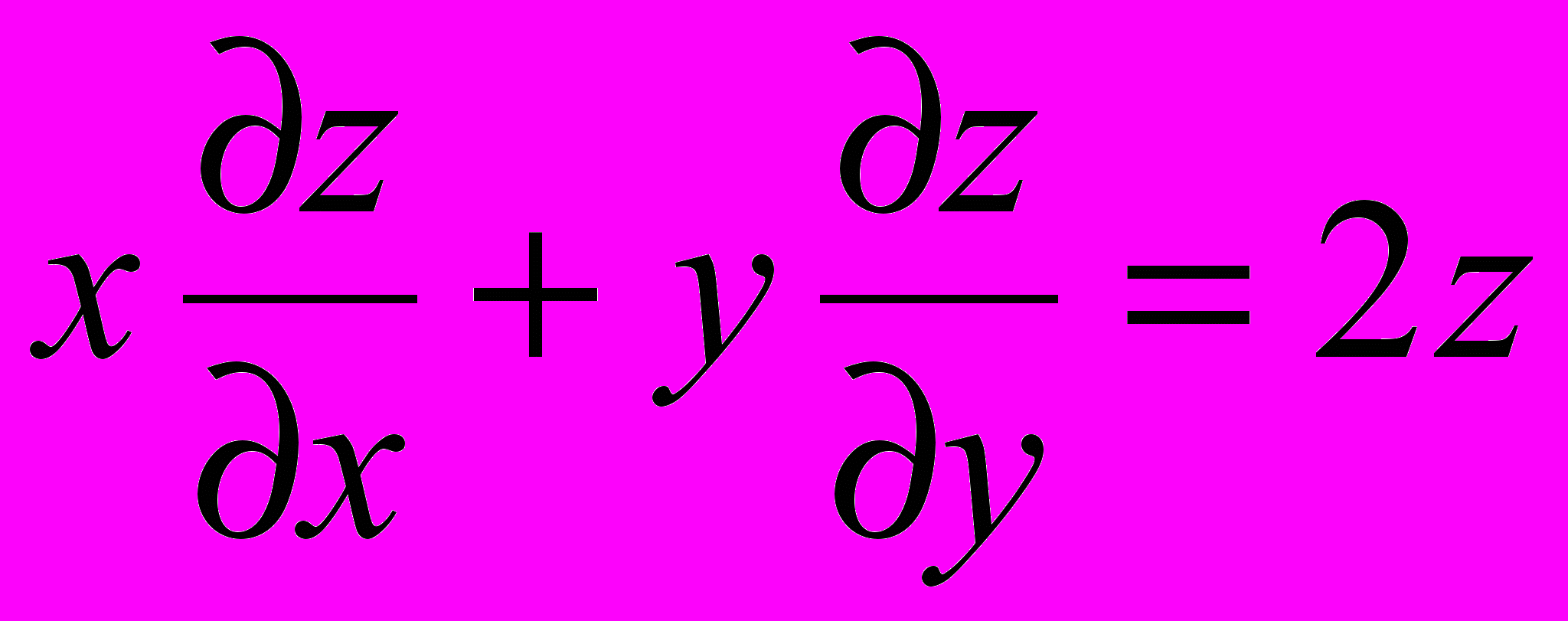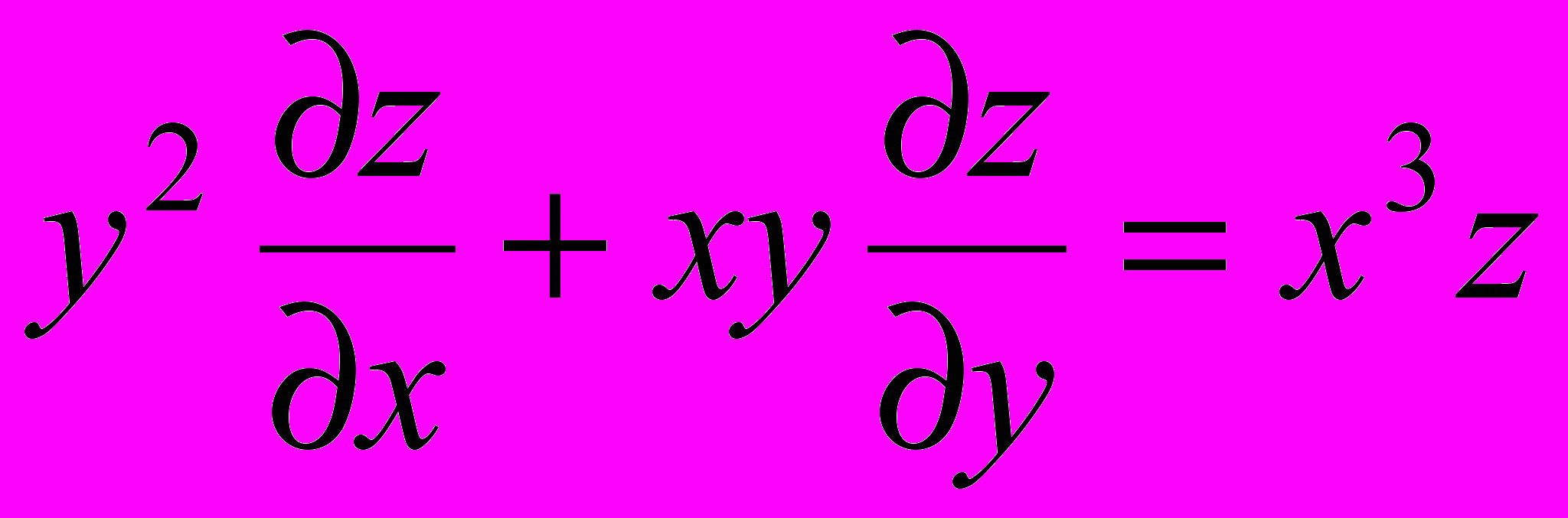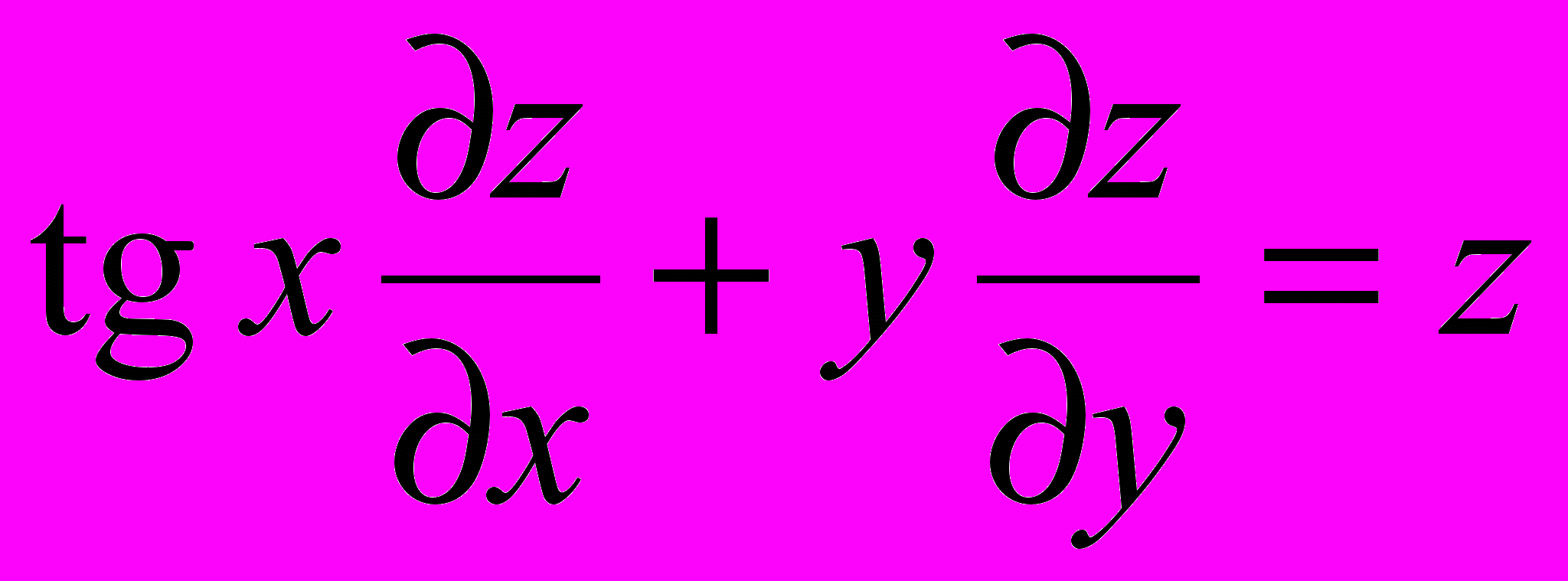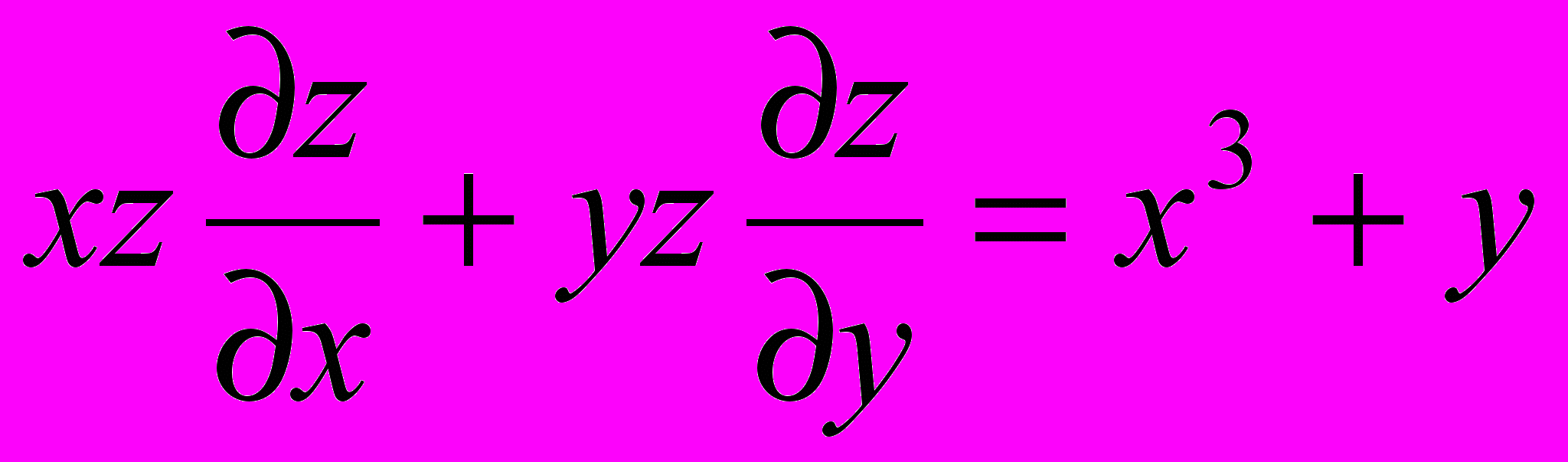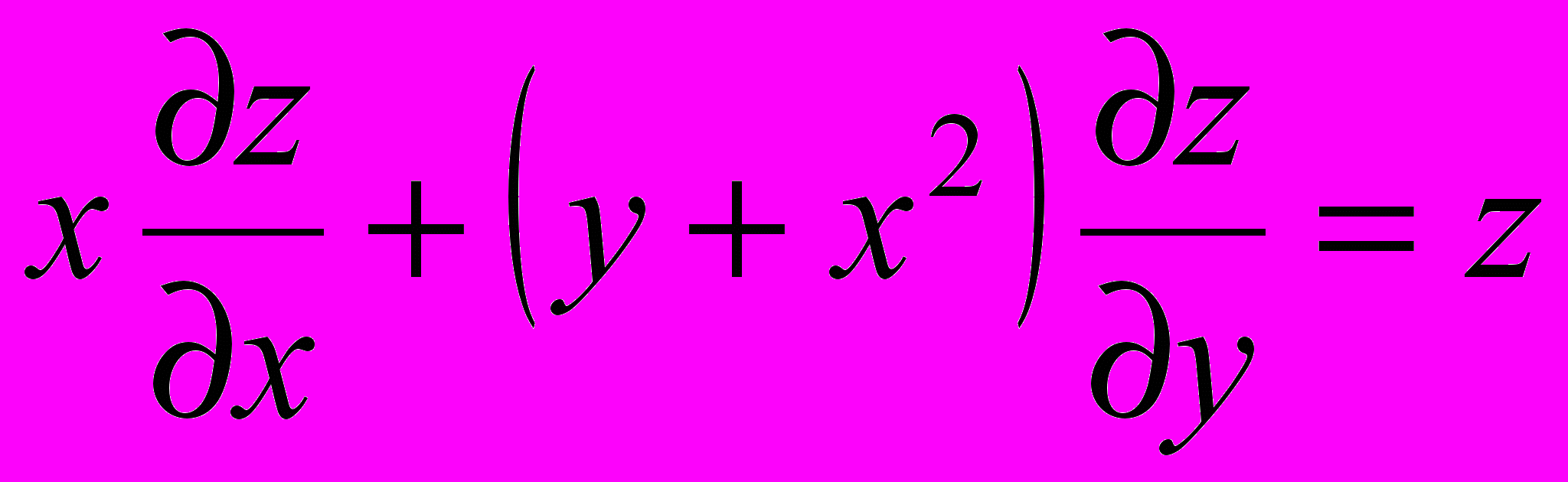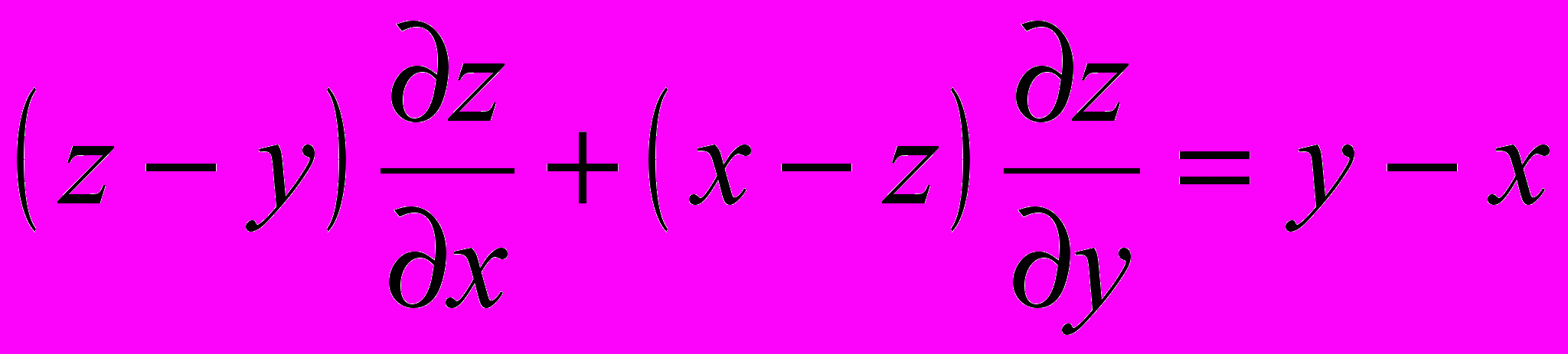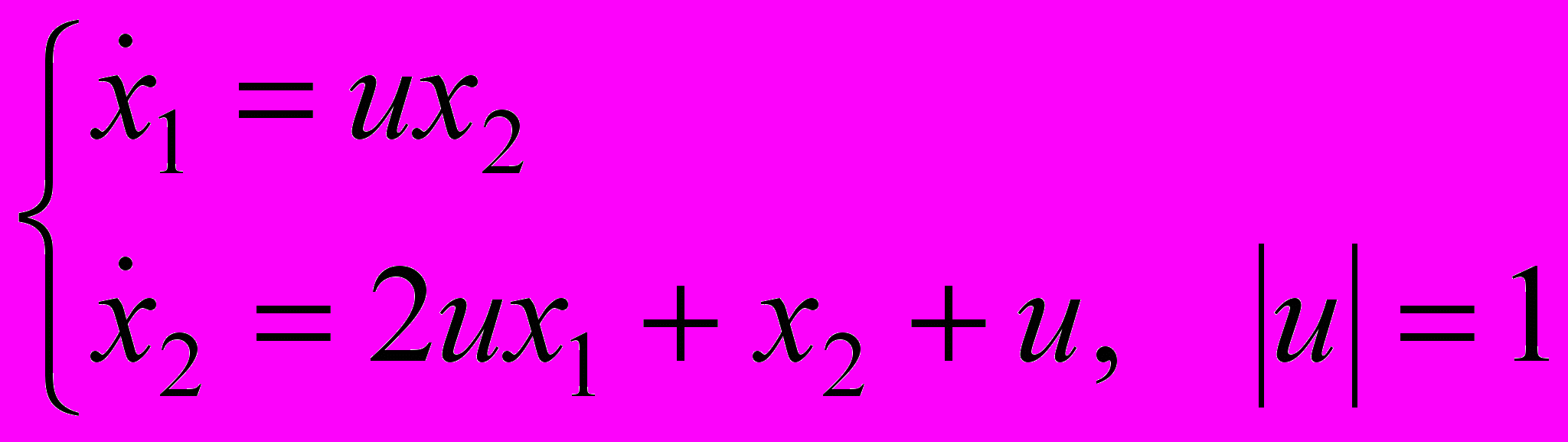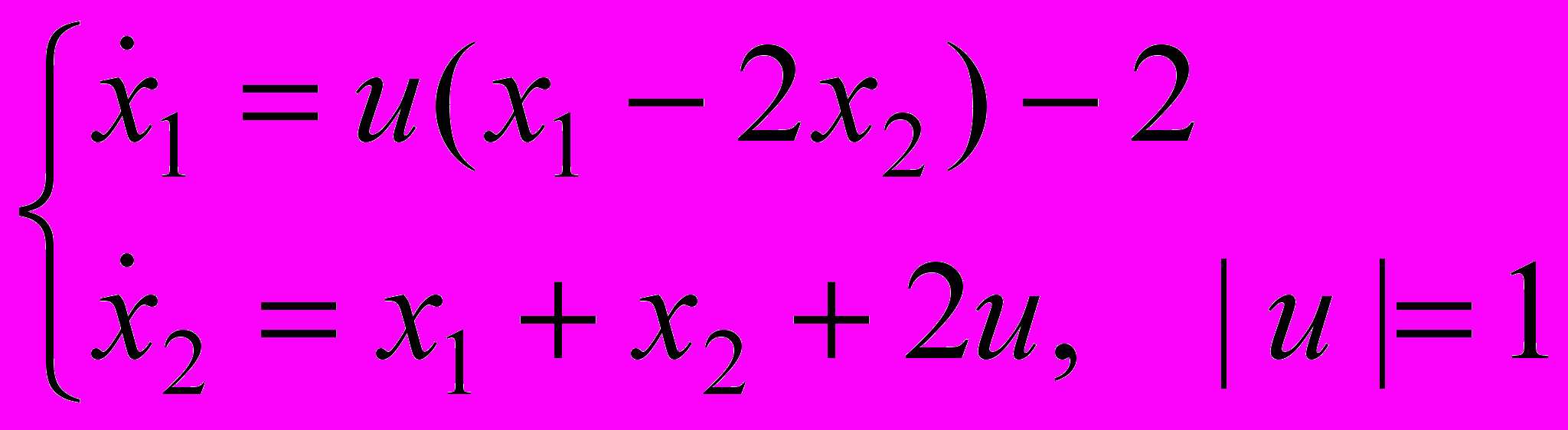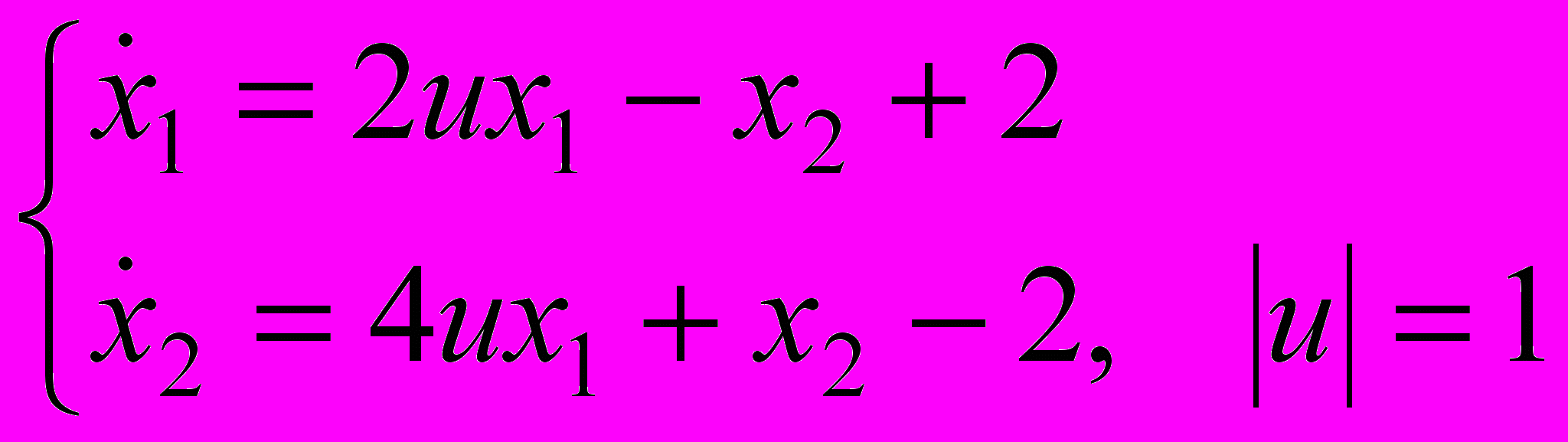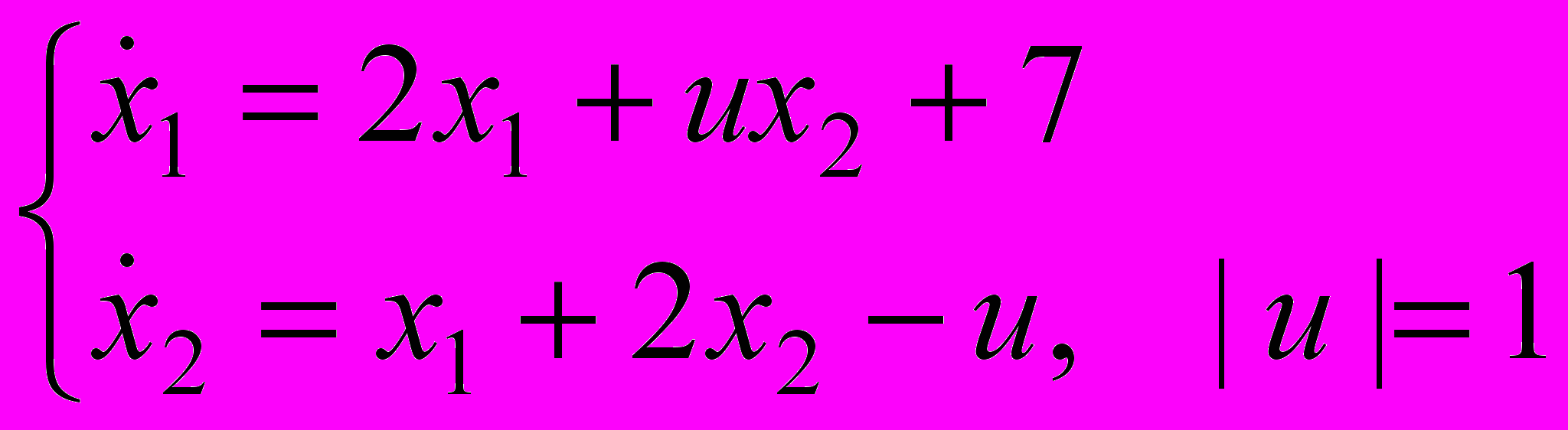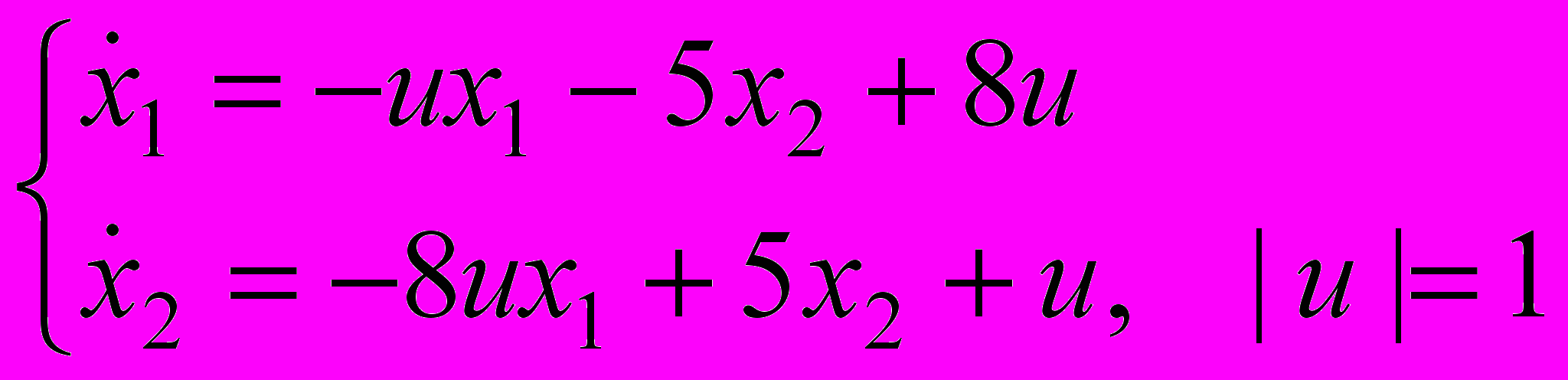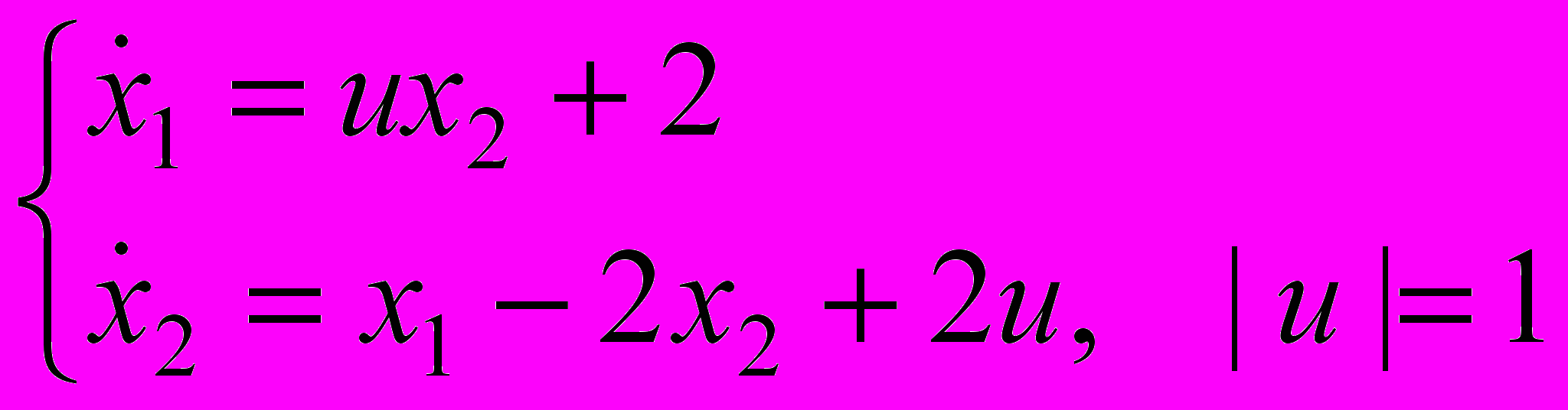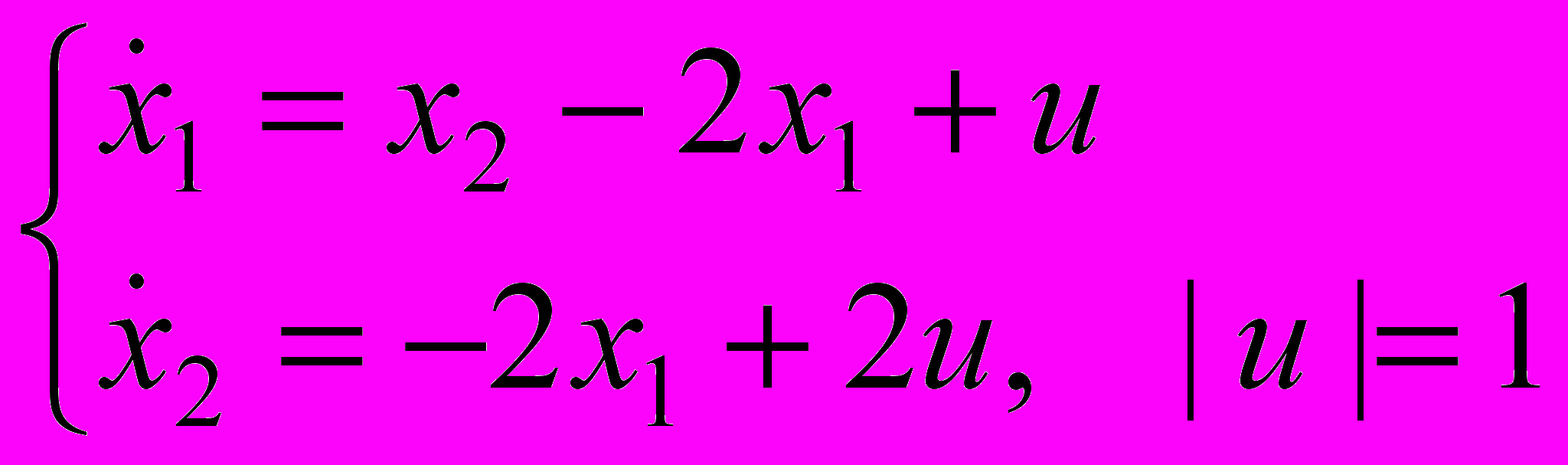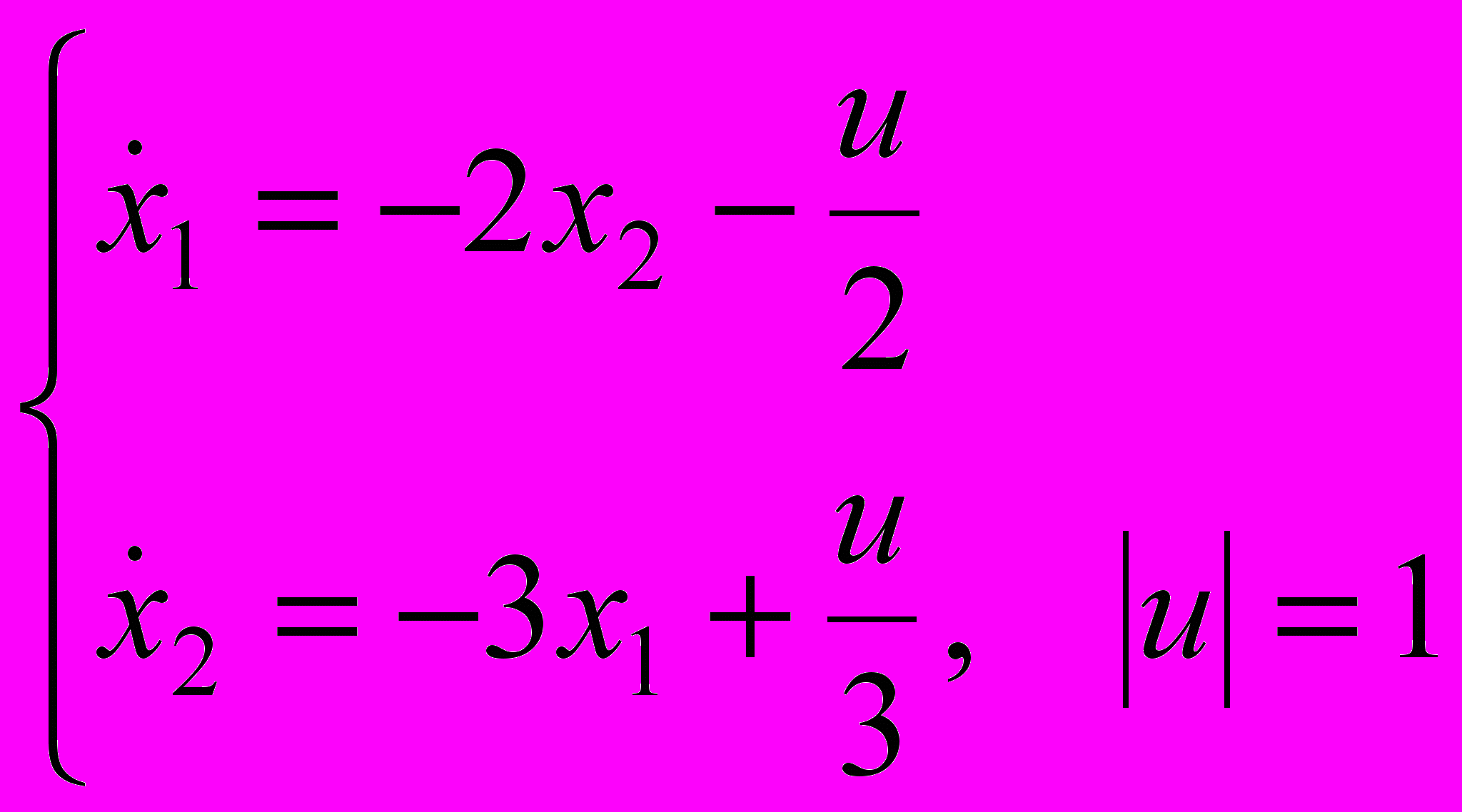Geum.ru

Содержание программы

Вид материалаРешение

Содержание


Непродолжаемые решения
Непрерывная зависимость решения от начальных условий
Дифференцируемость решения по параметру
Автономные системы дифференциальных уравнений и их фазовые пространства.
Первые интегралы
Теория устойчивости
Уравнения в частных производных первого порядка
Список дополнительной литературы
Рабочая программа
Кол-во часов
Вопросы к экзамену по учебной дисциплине
Государственное образовательное учреждение высшего
Синтез управления с не более, чем с одним переключением в управляемой системе второго порядка.
Подобный материал:

Содержание программы

3 семестр

Уравнения, неразрешенные относительно производной. Теорема существования и единственности решения, следствие. Дискриминантная кривая, особое решение дифференциального уравнения, неразрешенного относительно производной. Методы решения уравнений, неразрешенных относительно производной: разрешение относительно производной, метод введения параметра. Уравнения Лагранжа и Клеро.

Уравнения, допускающие понижение порядка. Промежуточные интегралы. Уравнения, не содержащие явно искомую функцию или независимое переменное. Понижение порядка в однородных уравнениях. Приведение к полной производной.

Непродолжаемые решения. Предложение о существовании непродолжаемого решения. Предложение о выходе непродолжаемого решения за границу ограниченного замкнутого множества, следствие для автономной системы. Пример.

Непрерывная зависимость решения от начальных условий и правой части уравнения. Теорема о непрерывной зависимости решения от правой части уравнения. Следствие о непрерывной зависимости решений от начальных условий. Теорема о непрерывной зависимости решения от параметра.

Дифференцируемость решения по параметру. Теорема о дифференцируемости решения по параметру, система уравнений в вариациях. Следствие о дифференцируемости решения по начальным значениям, система уравнений в вариациях. Теорема о дифференцируемости по параметру высоких порядков, следствие о разложении решения по степеням малого параметра.

Автономные системы дифференциальных уравнений и их фазовые пространства. Понятие автономной системы и нормальной автономной системы. Кинематическая интерпретация решения автономной системы. Совпадение двух траекторий. Положения равновесия и замкнутые кривые.

Фазовые пространства. Фазовые траектории. Критерий положения равновесия. Связь геометрической и кинематической интерпретаций решений нормальной системы.

Фазовая плоскость линейной однородной системы второго порядка с постоянными коэффициентами. Невырожденный случай. Вырожденный случай. Нулевые собственные значения. Система уравнений «Хищник-жертва».

Первые интегралы. Критерий первого интеграла. Функциональная независимость первых интегралов в области, ее связь с линейной независимостью. Теорема о существовании n независимых первых интегралов. Теорема о получении решения с помощью первых интегралов. Теорема о выражении любого первого интеграла через систему n независимых первых интегралов. Первые интегралы автономных систем, теорема о существовании n-1 независимого первого интеграла, не содержащего t.

Теория устойчивости: Устойчивость решения по Ляпунову, асимптотическая устойчивость по Ляпунову, связь этих понятий. Переход от исследования устойчивости произвольного решения к исследованию устойчивости нулевого решения. Достаточное условие устойчивости для линейной однородной системы с постоянными коэффициентами. Исследование устойчивости с помощью функций Ляпунова. Производная функции в силу системы уравнений. Теорема Ляпунова об устойчивости. Теорема Ляпунова об асимптотической устойчивости. Примеры. Теорема Четаева о неустойчивости. Пример. Теорема об устойчивости по первому приближению. Пример.

Уравнения в частных производных первого порядка: Линейные однородные уравнения первого порядка. Выражение решения через первые интегралы. Квазилинейные уравнения, характеристики. Задача Коши для квазилинейного уравнения. Теорема существования и единственности решения задачи Коши для квазилинейного уравнения в случае двух независимых переменных. Геометрический смысл условия существования и единственности.

Список рекомендуемой литературы
  1. Бибиков Ю.Н., Курс обыкновенных дифференциальных уравнений. М.: Высшая школа, 1991. 303с. (в наличии в библиотеке ЧелГУ)
  2. Краснов М.Л., Киселев Л.И., Макаренко Г.И., Обыкновенные дифференциальные уравнения: Задачи и примеры. М.: КомКнига, 2005. 256с.
  3. Петровский И.Г., Лекции по теории обыкновенных дифференциальных уравнений. М.: УРСС, 2003. 272с.
  4. Понтрягин Л.С., Обыкновенные дифференциальные уравнения. РХД, Москва, Ижевск, 2001. 400с. (в наличии в библиотеке ЧелГУ)
  5. Степанов В.В., Курс дифференциальных уравнений. М.: КомКнига/URSS, 2006. 472с. (в наличии в библиотеке ЧелГУ)
  6. Тихонов А.Н., Васильева А.Б., Свешников А.Г., Дифференциальные уравнения. М.: Наука, 1985. 231с. (в наличии в библиотеке ЧелГУ)
  7. Филиппов А.Ф.. Введение в теорию дифференциальных уравнений. М.: КомКнига, 2007. 240с.
  8. Филиппов А.Ф., Сборник задач по дифференциальным уравнениям. РХД, Москва, Ижевск, 2000. 175с. (в наличии в библиотеке ЧелГУ)
  9. Эльсгольц Л.Э. Дифференциальные уравнения. М.: КомКнига, 2006. 312с. (в наличии в библиотеке ЧелГУ)

Список дополнительной литературы

  1. Алеева С.Р., Белов Е.Г., Рольщиков В.Е., Ухоботов В.И., Методические указания к выполнению курсовых работ по дифференциальным уравнениям 2004. (электронный вариант на сайте кафедры).
  2. Арнольд В.И., Обыкновенные дифференциальные уравнения. М.: Наука, 1984. 240с. (в наличии в библиотеке ЧелГУ)
  3. Дмитриев В.И., Лекции по обыкновенным дифференциальным уравнениям. М.: КДУ, 2007. 220с.
  4. Зайцев В.Ф., Полянин А.Д., Справочник по обыкновенным дифференциальным уравнениям. М.: ФИЗМАТЛИТ, 2001. 576с.
  5. Камке Э., Справочник по обыкновенным дифференциальным уравнениям. М.: Наука, 1971. 576с.
  6. Матвеев Н.М., Методы интегрирования обыкновенных дифференциальных уравнений. Мн.: Высшая школа, 1974. 656с. (в наличии в библиотеке ЧелГУ)



Рабочая программа


№

Темы лекционных занятий (3 семестр)
Кол-во часов

1
Уравнения, неразрешенные относительно производной
1

2
Уравнения, допускающие понижение порядка.
1

3
Фазовая плоскость линейной однородной системы второго порядка с постоянными коэффициентами и консервативной системы.
2

4
Первые интегралы, уравнения с частными производными первого порядка.
3

5
Устойчивость. Теоремы Ляпунова и Четаева. Устойчивость по первому приближению.
4




Итого за семестр:
12




Всего:
24

Темы программы, вынесенные на самостоятельное изучение
3 семестр



1
Уравнения, неразрешенные относительно производной. Особые решения. Уравнения Лагранжа и Клеро.
4

2
Уравнения, допускающие понижение порядка.
2

3
Непродолжаемые решения.
10

4
Непрерывная зависимость решения от правой части уравнения, начальных значений и параметров.
10

5
Дифференцируемость решения по параметрам и начальным значениям. Уравнения в вариациях.
10

6
Устойчивость по Ляпунову. Теоремы Ляпунова и Четаева. Устойчивость по первому приближению.
8

7
Выполнение контрольной работы №2
16




Итого за семестр:
60




4 семестр



1
Автономные системы дифференциальных уравнений и их фазовые пространства. Кинематическая интерпретация решения автономной системы.
2

2
Фазовые траектории. Критерий положения равновесия.
2

3
Фазовая плоскость линейной однородной системы второго порядка с постоянными коэффициентами.
6

4
Фазовая плоскость консервативной системы с одной степенью свободы.
8

5
Система уравнений «Хищник-жертва».
4

6
Уравнения с частными производными первого порядка. Квазилинейные уравнения, характеристики. Задача Коши для квазилинейного уравнения.
8

7
Курсовая работа по дифференциальным уравнениям
30




Итого за семестр:
60

Методические указания студентам

Изучение каждой темы следует начинать с проработки соответствующего теоретического материала в учебниках [1], [4], [5], [7], [9] или использовать собственный конспект лекций данной дисциплины. Для усвоения теоретического материала также нужно разобрать предлагаемые в лекционном курсе примеры. Только затем следует закрепить разобранный материал изучаемой темы самостоятельным решением задач из [8].

Успешное написание контрольных работ возможно только при внимательном, всестороннем и качественном изучении соответствующих лекционных конспектов и текстов учебников. Решение задач контрольные работы оформляется в отдельной тетради с указанием фамилии студента, варианта задания, текста задач и полным, подробным решением.

Для успешного написания курсовой работы по дифференциальным уравнениям необходимо внимательно прочитать «Методические указания к выполнению курсовых работ по дифференциальным уравнениям»[1д] и изучить в необходимом объеме рекомендуемую литературу, при оформлении текста работы нужно придерживаться рекомендаций по каждой задаче курсовой работы, данных в методических указаниях. Оформление текста должно быть аккуратным, подробным, включать необходимые ссылки на использованную литературу.

Вопросы к экзамену по учебной дисциплине

«Дифференциальные уравнения», 4 семестр
  1. Уравнения, неразрешенные относительно производной. Теорема существования и единственности. Способы решения
  2. Уравнения, допускающие понижение порядка: уравнения, не содержащие явно искомой функции или независимого переменного, однородные уравнения, приведение к полной производной.
  3. Фазовая плоскость линейной однородной системы с постоянными коэффициентами.
  4. Первые интегралы. Критерий первого интеграла. Существование n независимых первых интегралов. Получение решения с использование первых интегралов.
  5. Выражение решения линейного и квазилинейного уравнения в частных производных через первые интегралы.
  6. Устойчивость решения, асимптотическая устойчивость.
  7. Достаточное условие устойчивости положения равновесия для линейной однородной системы с постоянными коэффициентами.
  8. Функция Ляпунова. Дифференцирование в силу системы уравнений.
  9. Теоремы Ляпунова об устойчивости и об асимптотической устойчивости.
  10. Теорема Четаева неустойчивости.
  11. Формулировка теорема Ляпунова об устойчивости по первому приближению.

Контрольная работа №2 по учебной дисциплине

«Дифференциальные уравнения» (сдается в 4 семестре)

  1. Решить уравнение, не разрешенное относительно производной:
  1. Понизить порядок уравнения и решить его:
  1. Найти общее решение уравнения в частных производных первого порядка:
  1. Определить характер положения равновесия (0,0), нарисовать фазовый портрет и исследовать на устойчивость:







    8. .

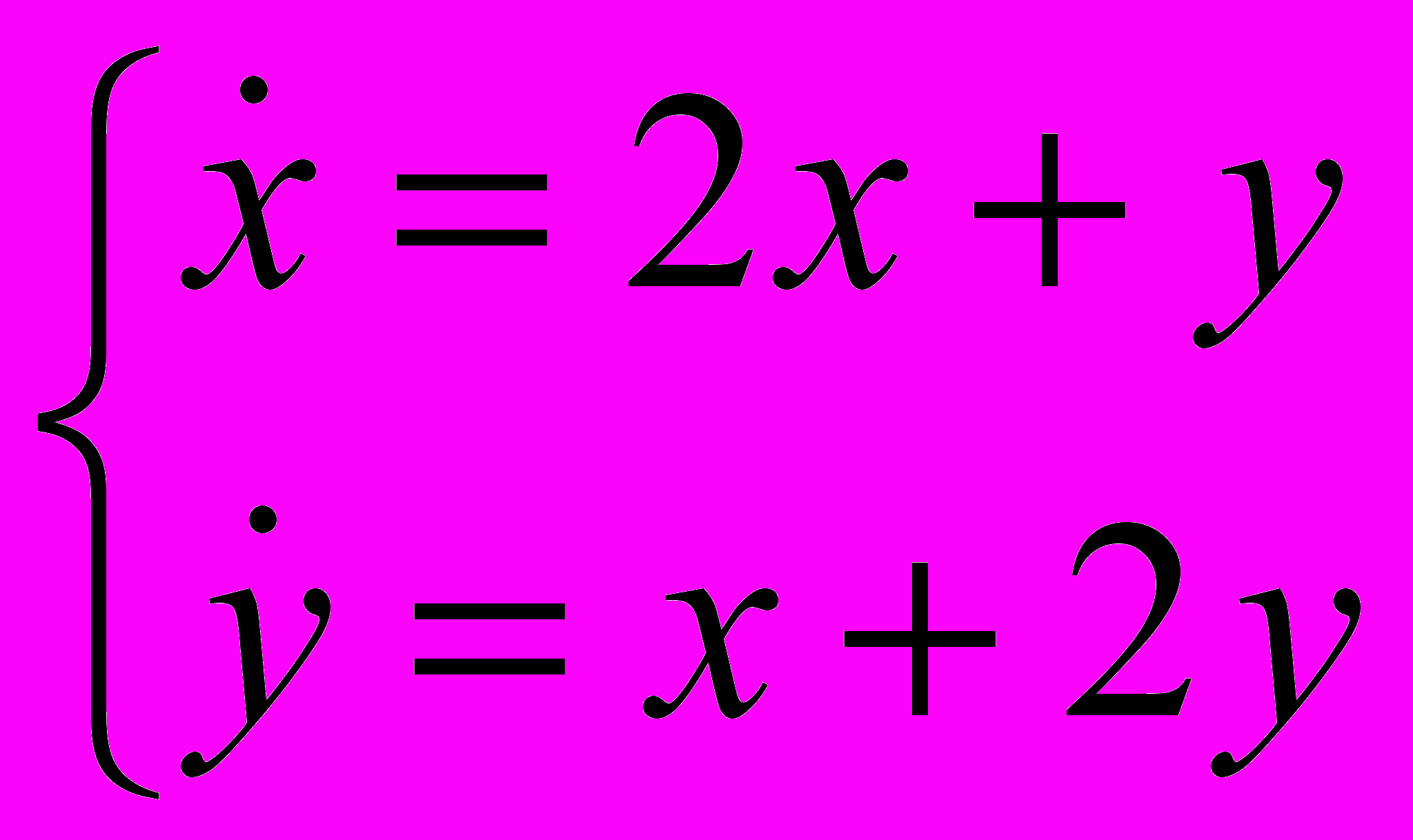
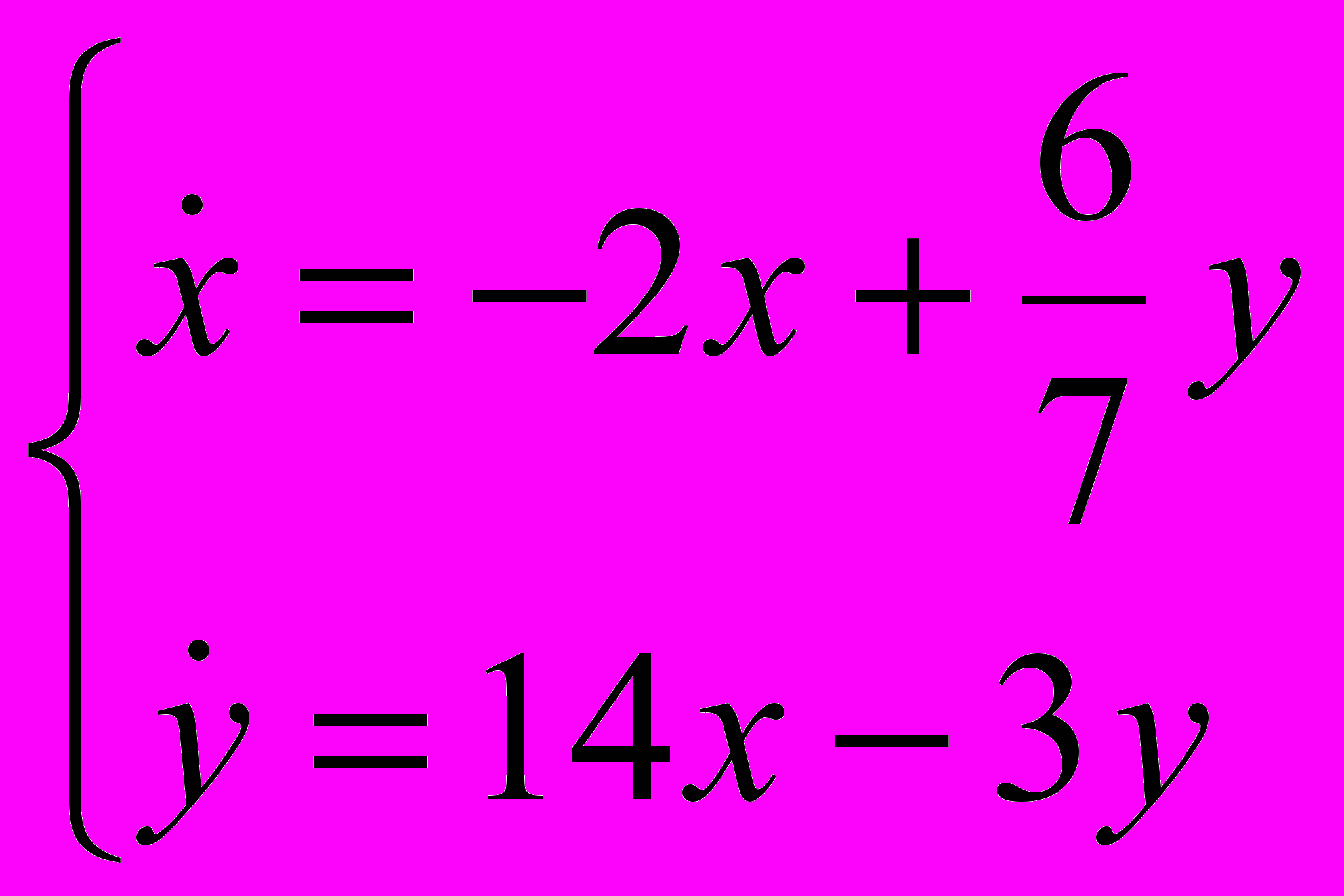
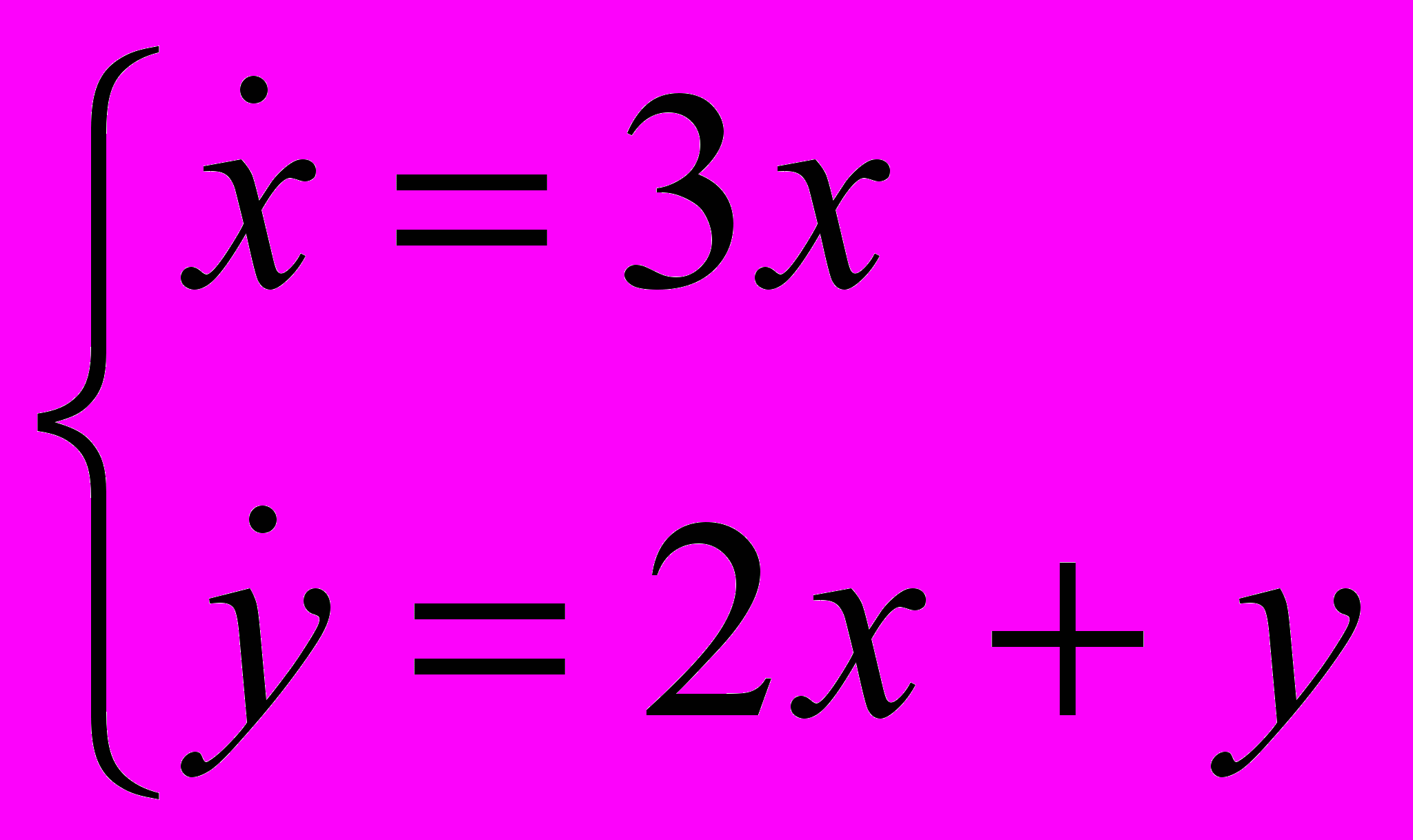
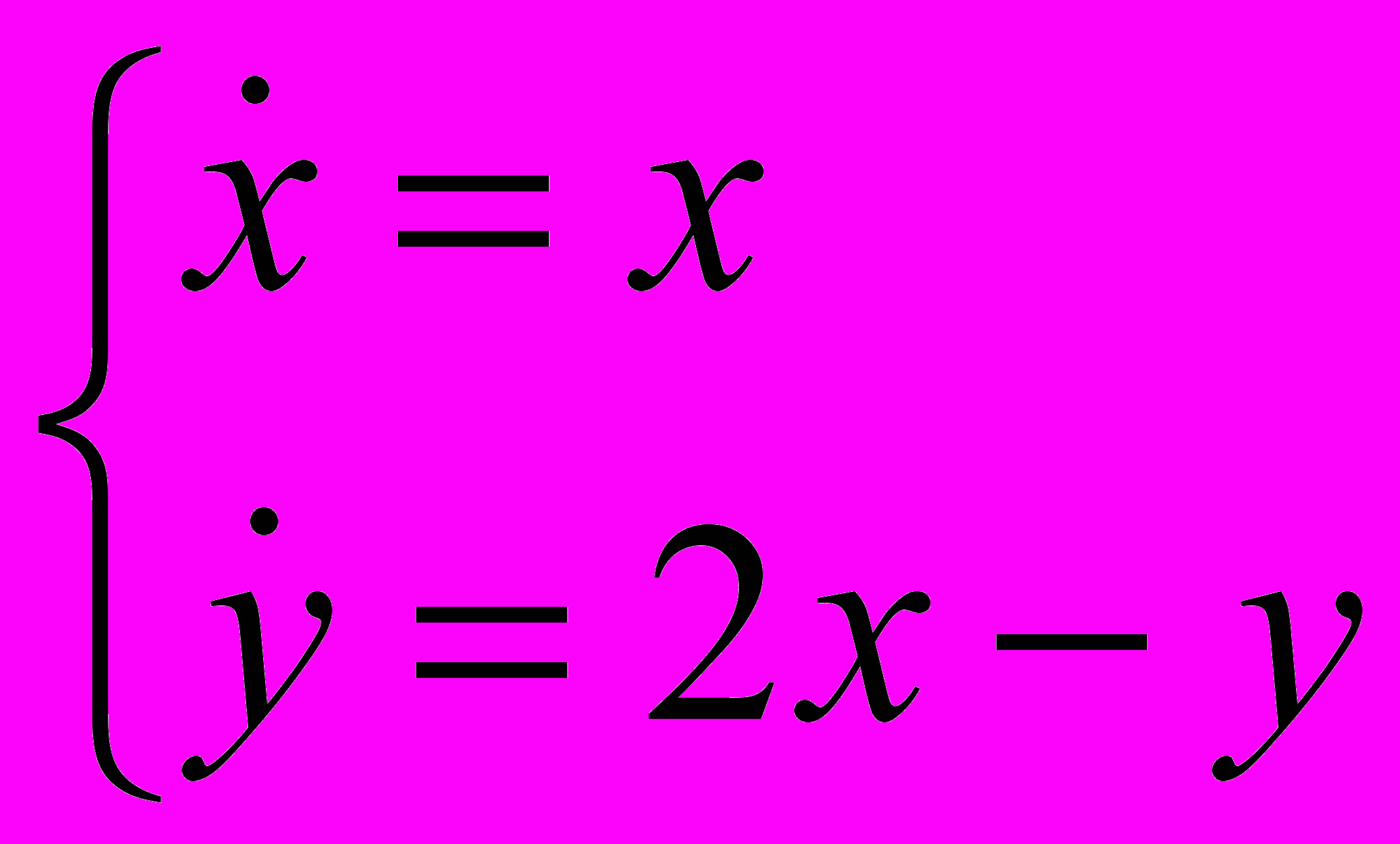
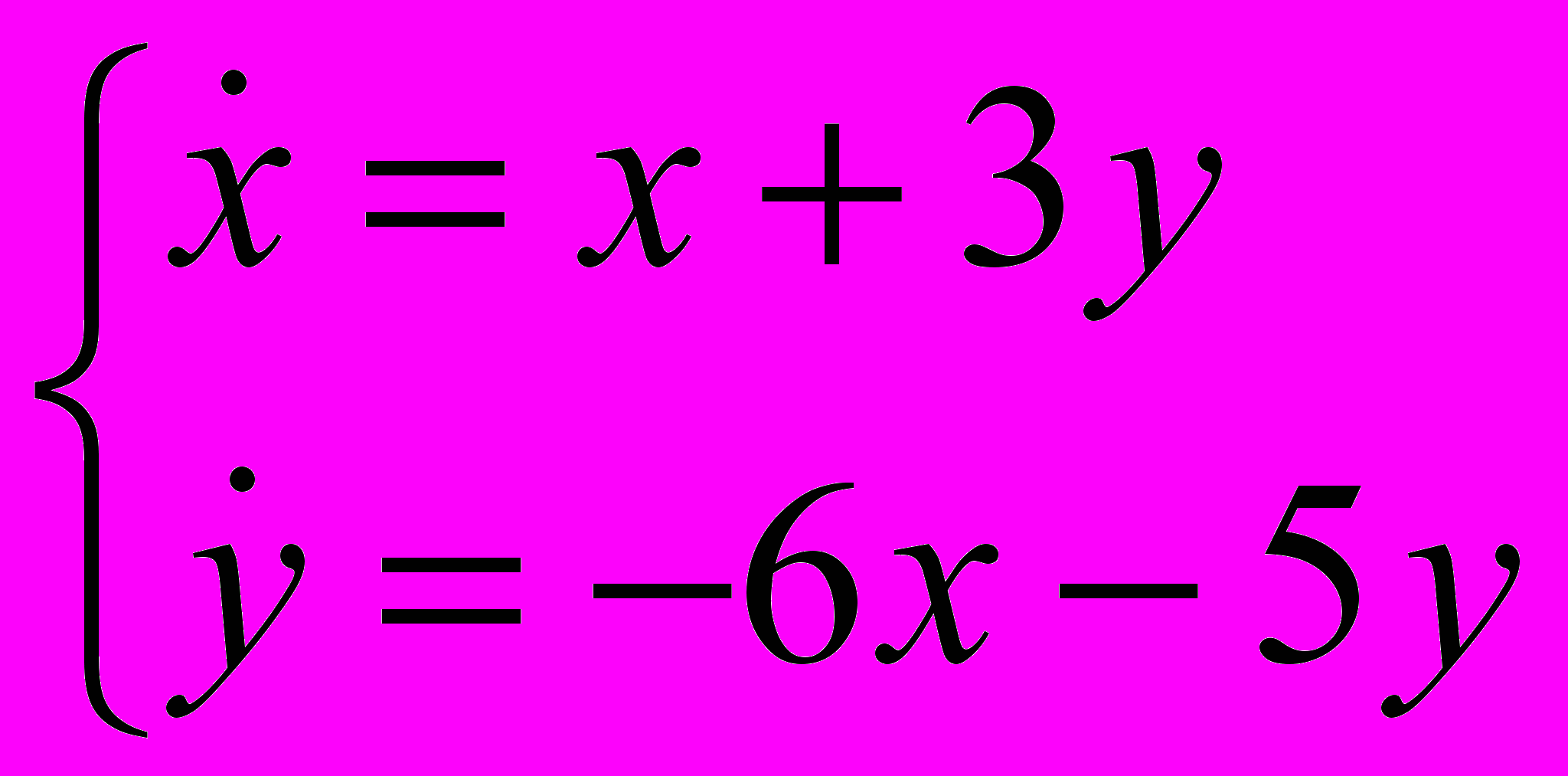
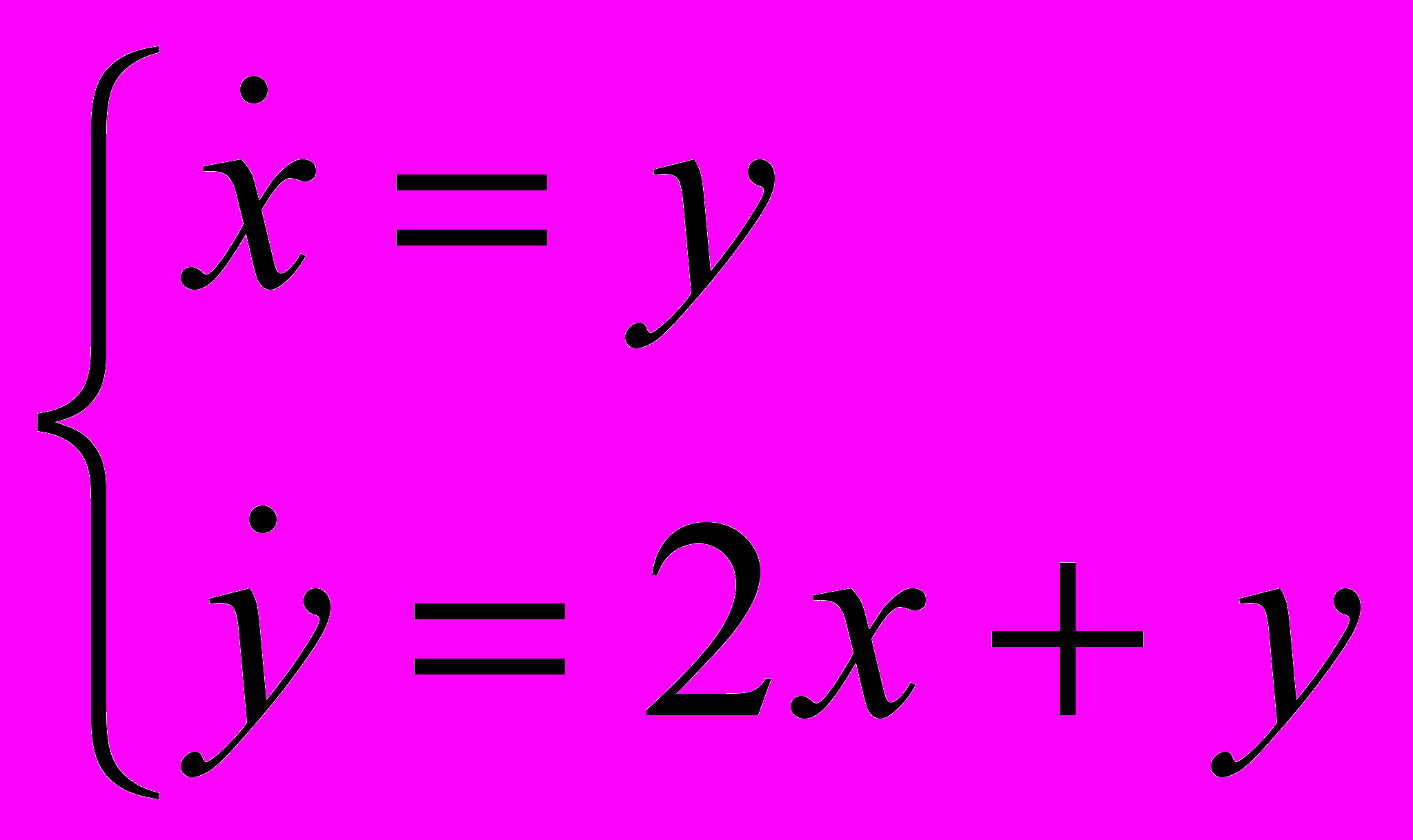
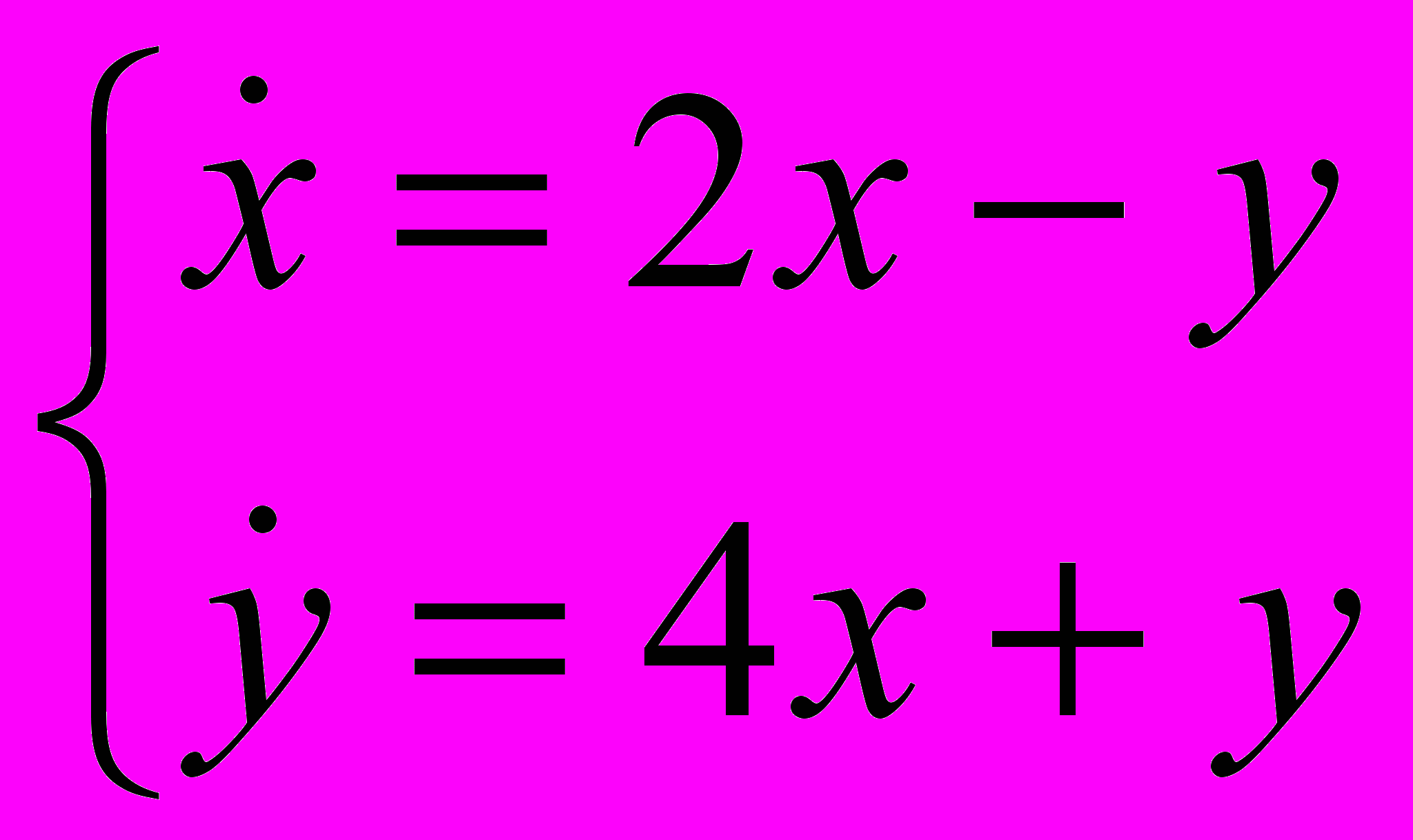
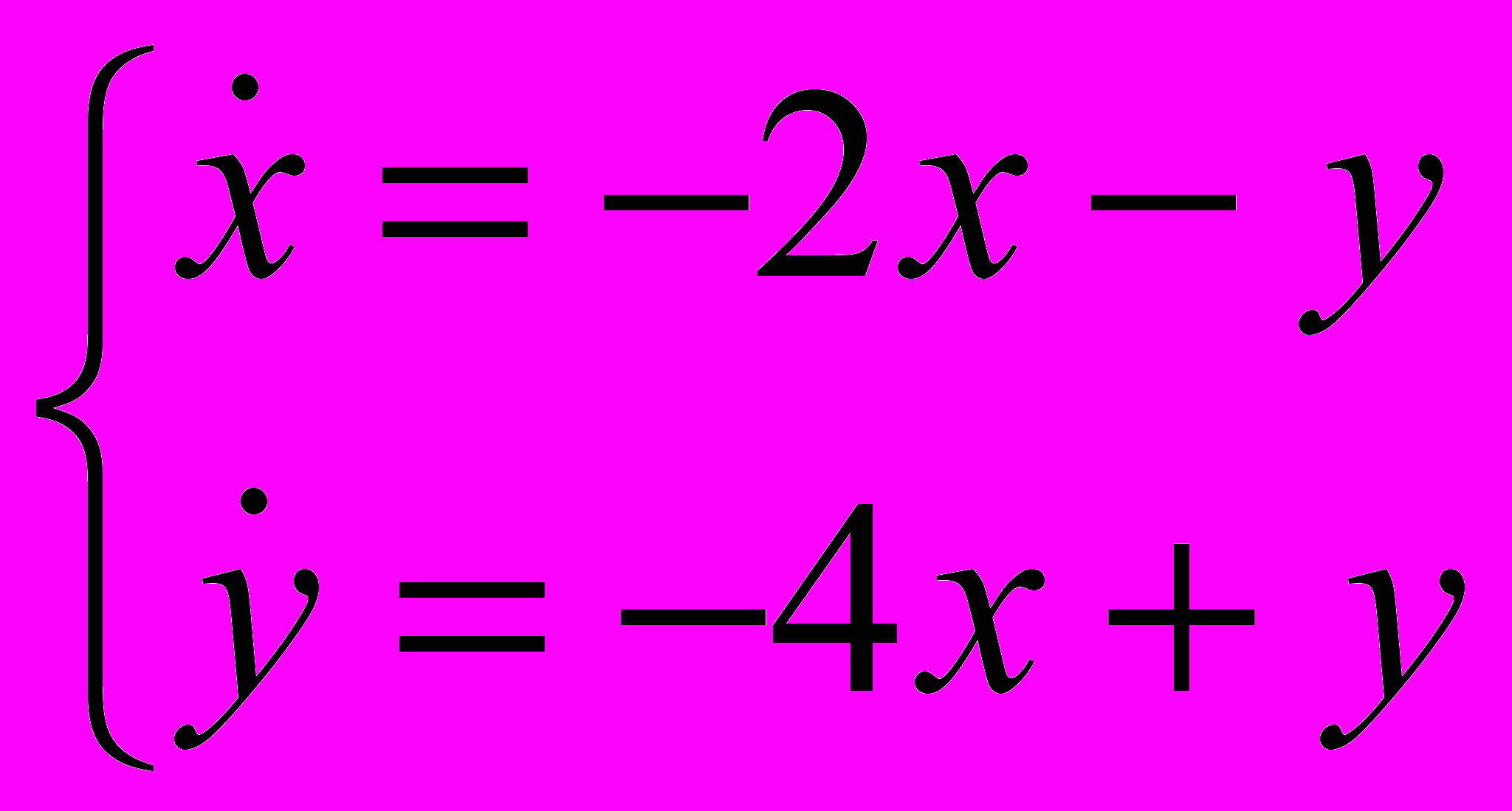Лектор__________________ доцент кафедры ТУиО, к. ф.-м. н. Алеева С.Р.

Федеральное агентство по образованию


Государственное образовательное учреждение высшего

профессионального образования


"Челябинский государственный университет"


Математический факультет

Кафедра теории управления и оптимизации


Методические указания к выполнению курсовых работ по

дифференциальным уравнениям


Составители: Алеева С. Р.

Белов Е. Г.

Рольщиков В. Е.

Ухоботов В. И.





Челябинск 2010



Синтез управления с не более, чем с одним переключением в управляемой системе второго порядка.

В курсовой работе рассматривается линейная управляемая система:

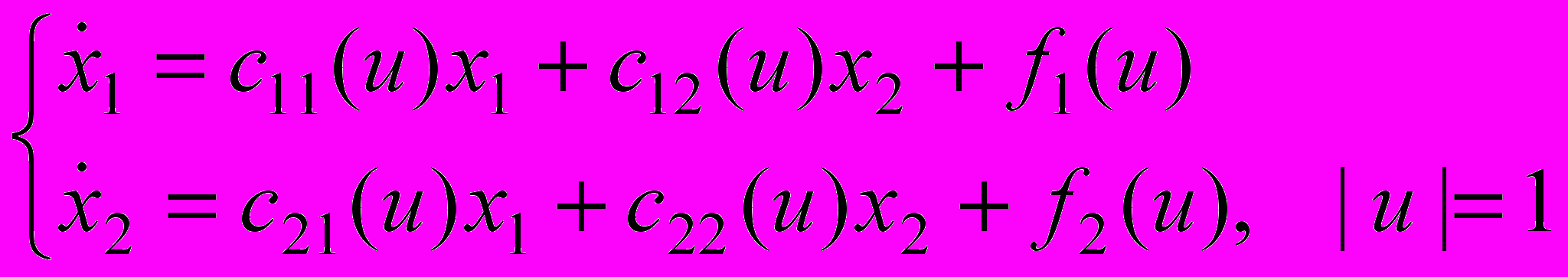
Требуется подобрать управление и(∙), переводящее фазовую точку (х1, х2) из заданного начального состояния в начало координат (0,0).

На выбор управления и(∙) накладывается условие | и(∙)|=1 и и(∙) имеет не более одного переключения.

Для решения поставленной задачи необходимо:
  1. Нарисовать фазовые портреты двух систем (отдельно при и1 и и-1), пояснив процесс построения.
  2. С помощью фазовых портретов осуществить синтез управления, указав линии переключения. Для этого совместить фазовые портреты при и1 и и-1 на одной координатной плоскости, изображая их разными цветами, линию переключения выделить;
  3. На фазовой плоскости выделить (заштриховать) область достижимости(все начальные положения, из которых возможно достижение точки (0,0) с управлением, имеющим не более одно переключения).

Методы построения фазовых портретов можно изучить в [1,2,5].

С теорией оптимального управления можно ознакомиться в [3,4].


Варианты курсовых работ

Литература

  1. Лизоркин Г.И. Курс обыкновенных дифференциальных и интегральных уравнений. М.: Наука, 1981, Гл.7. §6. С.344-348.
  2. Эльсгольц Г.Э. Дифференциальные уравнения и вариационное исчисление. М.: Наука, 1969, Гл.2. §7.
  3. Понтрягин Л.С., Болтянский В.Г., Гамкрелидзе Р.В., Мищенко Е.Ф. Математическая теория оптимальных процессов. М.: Наука, 1969, Гл.1. §5.
  4. Болтянский В.Г. Математические методы оптимального управления. М.: Наука, 1969, Гл.1. §3.
  5. Понтрягин Л.С. Обыкновенные дифференциальные уравнения. М.: Наука, 1974, Гл.2. §16.