Раздзел VI. Навучанне разважанням
| Вид материала | Документы |
- Раздзел I. Асновы канстытуцыйнага ладу (артыкулы 1 20) раздзел, 554.42kb.
- Раздзел I. Старажытнае грамадства на тэрыторыі беларусі. Фарміраванне этнічных супольнасцей, 6321.57kb.
- Публикация Журнал «Пачатковае навучанне: сям я, дзіцячы сад, школа», 105.64kb.
- Планы- канспекты творчых урокаў І прадметных тыдняў Гісторыя Беларусі, 1850.94kb.
- Раздзел Выкарыстанне асобасна-арыентаваных тэхналогій навучання, 855.87kb.
- Тлумачальная запіска, 170.51kb.
- Тлумачальная запіска, 170.54kb.
- Раздзел Нетрадыцыйныя формы ўрокаў, 388.54kb.
- Нормы ацэнкі вынікаў вучэбнай дзейнасці вучняў па вучэбным прадмеце «Беларуская мова», 489.22kb.
Разгледзім наступнае правільнае разважанне:
"Калі ўсе пасылкі праўдзівыя і разважанне праведзена па лагічных правілах, то і заключэнне праўдзівае. У выніку разважання атрымалі непраўдзівае заключэнне. Значыць, не ўсе пасылкі праўдзівыя або разважанне праведзена не па правілах вываду".
3 дадзенага разважання вынікае, што прычынамі памылак у разважаннях могуць быць:
1) непраўдзівасць хоць бы адной з пасылак;
2) адступленне ад правіл лагічнага вываду.
Таму вызначэнне правільнасці правядзення разважання прадугледжвае наступныя крокі:
а) праверка праўдзівасці пасылак;
б) праверка на адпаведнасць спосабу пераходу ад пасылак да заключэння па пэўнаму правілу лагічнага вываду.
Зразумела, калі высвятляецца, што нейкая з пасылак разважання непраўдзівая, то адразу ж, без далейшай праверкі, можна ўпэўнена сцвярджаць, што разважанне няправільнае. Напрыклад,
"Калі лік меншы за 10, то ён цотны. Лік 7 < 10. Значыць, 7 - цотны лік".
Вялікая пасылка ў гэтым разважанні непраўдзівая, таму разважанне няправільнае.
У выпадку, калі ўсе пасылкі праўдзівыя, неабходна перайсці да вызначэння спосабу разважання і яго адпаведнасці аднаму з правіл лагічнага вываду. Напрыклад, у наступным разважанні ўсе пасылкі праўдзівыя, але заключэнне непраўдзівае, г. зн. разважанне няправільнае.
"Калі птушка ўмее лятаць высока ў небе, то ў яе ёсць крылы. У курыцы ёсць крылы. Значыць, курыца ўмее лётаць высока ў небе".
Атрыманае заключэнне "Курыца ўмее лятаць высока ў небе" відавочна непраўдзівае, хоць вялікая і малая пасылкі праўдзівыя Дадзенае разважанне няправільнае таму, што яно праведзена не па правілу заключэння (1), а па спосабу, які не гарантуе праўдзівасці заключэння. Выразна вылучыць гэты спосаб дазваляе запіс разважання ў схематычным выглядзе (2). Параўнайце яго з правілам заключэння.
А В А В
А (1) В____ (2)
В А
Па схеме (2) разважаць нельга, таму што можна атрымаць непраўдзівае заключэнне. Ці правільным будзе наступнае разважанне?
"Калі чалавек прымяняе правілы вываду, то ён разважае правільна. Вольга разважае правільна. Значыць, Вольга прымяняе правілы вываду".
Па якой схеме праведзена гэта разважанне - па схеме (1) ці па схеме (2)? Разважанне пабудавана па схеме (2) і, значыць, з'яўляецца няправільным. Сапраўды, магчыма, што Вольга, як і многія іншыя людзі, інтуітыўна разважае правільна нават у тым выпадку, калі ніколі не чула аб правілах лагічнага вываду.
Каб выправіць памылку ў разважанні, трэба адмовіцца ад схемы (2) і перайсці да схемы (1), якая з'яўляецца правілам вываду:
"Калі чалавек прымяняе правілы вываду, то ён разважае правільна. Вольга прымяняе правілы вываду. Значыць, Вольга разважае правільна".
Атрыманае заключэнне бясспрэчна праўдзівае. Роля правіл вываду менавіта ў тым і заключаецца, што ад праўдзівых пасылак яны заўсёды вядуць да праўдзівага заключэння. Так, разважанне аб птушках выпраўляецца наступным чынам:
"Калі птушка ўмее лятаць высока ў небе, то яна мае крылы. Арол умее лятаць высока ў небе. Значыць, у арла ёсць крылы.
Разважанне можа аказацца няправільным і ў тым выпадку, калі ўсе пасылкі, а таксама заключэнне з'яўляюцца праўдзівымі. Напрыклад:
"Калі лік дзеліцца на 15, то ён дзеліцца на 3. Лік 45 дзеліцца на 3. Значыць, лік 45 дзеліцца на 15".
Пасылкі і заключэнне ў гэтым разважанні праўдзівыя, але яно няправільнае таму, што праведзена па схеме (2), а не па схеме (1). Недапушчальнасць такой формы разважання даказваецца метадам прывядзення контрпрыкладу: па гэтай форме з праўдзівых пасылак можна атрымаць непраўдзівае заключэнне, Знойдзем падыходзячы контрпрыклад:
"Калі лік дзеліцца на 15, то ён дзеліцца на 3. Лік 48 дзеліцца на 3. Значыць, лік 48 дзеліцца на 15" [13, с. 147].
Усе пасылкі ў апошнім разважанні праўдзівыя. Яго форма тая ж самая, што і ў разважанні аб ліку 45, а заключэнне "Лік 48 дзеліцца на 15" з'яўляецца непраўдзівым. Такім чынам, мы даказваем вучням, што разважанні па схеме (2) недапушчальныя.
Ва ўсіх практыкаваннях, якія прыводзяцца ў дадзеным параграфе, патрабуецца знайсці памылку ў разважаннях і выправіць яе. Нагадаем, што для гэтага неабходна праверыць:
1) праўдзівасць пасылак;
2) адпаведнасць правілу лагічнага вываду.
Пры выкананні заданняў пажадана выкарыстоўваць карткі з каляровымі сігналамі і схемы правільных разважанняў.
ПРАКТЫКАВАННІ
СВЕТ ВАКОЛ НАС
1. Калі ў чалавека высокая тэмпература, то ён хворы.
Каця хворая._______________
У Каці высокая тэмпература.
Адказ. Заключэнне непраўдзівае таму, што хвароба можа працякаць без павышэння тэмпературы. Памылка ў форме разважання.
2. Калі ў чалавека высокая тэмпература, то ён хворы.
У Каці нармальная тэмпература.
Каця няхворая.
Адказ. Заключэнне непраўдзівае. Памылка ў форме разважання. Правільнае разважанне: "Калі ў чалавека высокая тэмпература, то ён хворы. У Каці высокая тэмпература. Значыць, Каця хворая".
3. Усе людзі адукаваныя.
Сідараў неадукаваны.
Сідараў - нечалавек.
Адказ. Заключэнне непраўдзівае таму, што вялікая пасылка непраўдзівая - сярод людзей ёсць і неадукаваныя.
4. Усе піяністы - музыканты.
Іваноў - музыкант.
Іваноў - піяніст.
Адказ. Заключэнне непраўдзівае таму, што Іваноў можа быць скрыпачом, ударнікам і г. д. Памылка ў малой пасылцы. Яна павінна быць суджэннем аб піяністах, а не аб музыкантах.
- Калі сёння пятніца, то заўтра субота.
Сёння чацвер.
Заўтра пятніца
Адказ. Памылка ў малой пасылцы, яна не мае лагічнай сувязі з вялікай пасылкай.
МАТЭМАТЫКА
1. Калі лік двухзначны, то ён цотны.
71 - двухзначны лік.
71 - цотны лік.
2. Калі скласці два цотныя лікі, то сума таксама будзе цотным лікам.
Сума лікаў 7 і 13 роўна 20. 20 - цотны лік._____________
Лікі 7 і 13 - цотныя лікі.
Адказ. Разважанне праведзена не па правілу.
3. Калі множнікі памяняць месцамі, то здабытак не зменіцца.
Здабыткі роўныя.__________________________________
Множнікі памянялі месцамі.
Контрпрыклад: 6 • 4 = 24 і 8 • 3 = 24. Здабыткі роўныя, а множнікі розныя. Разважанне праведзена не па правілу.
4. Калі квадрат разрэзаць на 2 роўныя часткі, то яго плошча паменшыцца ў 2 разы.
Плошчу квадрата зменшылі ў 2 разы.
Квадрат разрэзалі на 2 роўныя часткі.
Адказ. Разважанне праведзена не па правілу. Заключэнне непраўдзівае - паменшыць плошчу квадрата ў 2 разы можна, і не разразаючы яго. Напрыклад, намаляваць адпаведныя фігуры.
5. Калі ў задачы атрымалі правільны адказ, то задачу рашылі правільна.
У задачы атрымалі правільны адказ._________________
Задачу рашылі правільна.
Адказ. Вялікая пасылка непраўдзівая, таму што правільны адказ можна атрымаць, зрабіўшы нават некалькі памылак у рашэнні.
6. Калі ўсе складаемыя аднолькавыя, то складанне можна замяніць множаннем.
15 + 15 + 15 + 5. Усе складаемыя аднолькавыя._______
Складанне можна замяніць множаннем:
15+ 15 + 15 + 5 = 15 -4.
Адказ. Малая пасылка непраўдзівая.
7. Калі ў трохвугольніка ёсць прамы вугал, то два астатнія вуглы вострыя.
У трохвугольніка АВС ёсць два вострыя вуглы.________
У трохвугольніка АВС трэці вугал прамы.
Контрпрыклады: востравугольны або тупавугольны трохвугольнікі. Разважанне праведзена не па правілу.
8. Калі дзве прамыя ўзаемна перпендыкулярныя, то яны перасякаюцца.
П
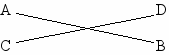
рамыя АВ і СD перасякаюцца.___________________
Прамыя АВ і СD узаемна перпендыкулярныя.
Контрпрыклад:
Разважанне праведзена не па правілу.
9. [13, с. 204].
Калі першы лік большы за другі, а другі лік большы за трэці, то першы лік большы за трэці. 122 > 211, а 211 > 125.
122 > 125.
Адказ. Малая пасылка непраўдзівая.
10. [13, с. 209].
Калі а і b адназначныя лікі, то а • b < 82.
8 • 7 < 82._______________
8 і 7 - адназначныя лікі.
Адказ. Разважанне праведзена не па правілу.
11. Калі лік дзеліцца на 2, то ён дзеліцца на 4.
12 дзеліцца на 2.
12 дзеліцца на 4.
Адказ. Вялікая пасылка непраўдзівая.
Контрпрыклад: 6 дзеліцца на 2, але 6 не дзеліцца на 4.
Заўвага. На падставе аналізу лагічна памылковых адказаў вучняў настаўнік мае магчымасць самастойна складаць падобныя лагічныя практыкаванні па ўсіх прадметах.
§ 4. Прапедэўтыка дэдуктыўнага доказу
Звычайна, калі гавораць аб ролі матэматыкі ў развіцці і выхаванні дзяцей, падкрэсліваюць яе ўплыў на фарміраванне такіх якасцей мыслення, як дакладнасць, строгасць, крытычнасць, лагічная паслядоўнасць, адцягненасць (абстрактнасць), абагульненасць і інш. Усё гэта з'яўляецца адбіткам дэдуктыўнага метаду, якім карыстаецца навука матэматыка.
Сутнасць дэдуктыўнага метаду - у наступным: пасля таго як у пэўнай галіне матэматыкі абраны зыходныя паняцці і сфармуляваны аксіёмы, яе выкладанне і далейшае развіццё ідзе шляхам чыстага, г. зн. заснаванага толькі на законах логікі, разважання. 3 аксіём і азначэнняў выводзяць тэарэмы; абапіраючыся на іх, даказваюць новыя тэарэмы і г. д. Атрыманыя такім чынам ісціны не выклікаюць сумненняў, таму што яны маюць лагічнае абгрунтаванне, іншымі словамі, іх праўдзівасць даказалі. 3 гэтай прычыны навучанне матэматыцы абавязкова звязана з навучаннем дэдуктыўнаму доказу.
У завершаным выглядзе дэдуктыўны доказ паўстае ў якасці канечнай паслядоўнасці суджэнняў дадзенай тэорыі, якія звязаны паміж сабой як па зместу, так і адносінамі лагічнай выніковасці.
Лагічную аснову змястоўных дэдуктыўных доказаў складаюць правілы вываду. Але, каб даказваць, недастаткова ведаць гэтыя правілы (іх можна нават і не ведаць!). Для гэтага неабходны пэўныя лагічныя ўменні, якія заключаюцца ў наступным:
1) рабіць, хаця б інтуітыўна, лагічныя вывады з зыходных суджэнняў;
2) адбіраць адпаведныя аргументы для доказу праўдзівасці суджэння;
3) даваць крытычную ацэнку змястоўным і лагічным сувязям паміж суджэннямі, якія ўваходзяць у дэдуктыўны доказ.
У некаторай ступені гэтыя ўменні вучні набываюць у час работы з правіламі вываду, але ў пачатковым навучанні (і не толькі матэматыцы) ёсць магчымасць паглыбіць і ўзмацніць падрыхтоўку мыслення дзяцей да дэдуктыўнага доказу. Губляць гэту магчымасць - значыць ісці супраць прыроды чалавека, бо шматлікія даследаванні псіхолагаў сведчаць, што асновы доказнага мыслення закладваюцца менавіта ў малодшым школьным узросце.
Прапануем настаўніку шэраг традыцыйных і нетрадыцыйных заданняў, аб'яднаных агульнай мэтай - фарміраваць у вучняў асновы доказнага мыслення. У адпаведнасці з вылучанымі ўменнямі, якія ўваходзяць у склад умення праводзіць дэдуктыўны доказ, усе заданні падзелены па іх асноўнай мэце на тры групы:
- фарміраванне ўмення рабіць лагічныя вывады з зыходных суджэнняў;
- навучанне абгрунтаванню праўдзівасці суджэнняў;
- пабудова лагічнай паслядоўнасці з дадзеных суджэнняў.
I. Мэта - фарміраванне ўмення рабіць лагічныя вывады з зыходных суджэнняў
Гульня "Хто ў якой хатцы жыве?"
Ж
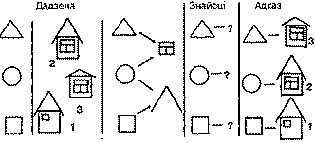
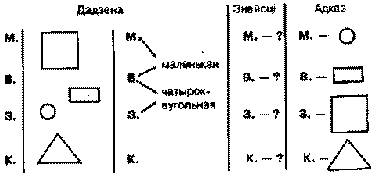
ылі-былі тры фігуры: трохвугольнік, круг, квадрат. I ў кожнай з іх была свая хатка. Адна хатка была з высокім дахам і маленькім акном, другая - з высокім дахам і вялікім акном, а трэцяя - з нізкім дахам і вялікім акном. Трохвугольнік і круг жывуць у хатках з вялікім акном, а круг і квадрат - у хатках з высокім дахам. У якой хатцы жыве кожная з фігур? [4, с. 32 - 35.]
Схематычны запіс умовы і патрабавання робіцца на дошцы загадзя ці адначасова з аналізам зместу лагічнага задання, якое выконваецца ў час гульні. Пошук адказу на пытанне "У якой хатцы жыве кожная з фігур?" зводзіцца да пабудовы лагічных вывадаў з умовы задачы.
1) Круг жыве ў хатцы з вялікім акном. Круг жыве ў хатцы з высокім дахам. Значыць, круг жыве ў хатцы з высокім дахам і вялікім акном (хатка 2).
2) Трохвугольнік жыве ў хатцы з вялікім акном. Такіх хатак дзве (2 і 3). У адной з іх (2) жыве круг. Значыць, трохвугольнік жыве ў хатцы 3. Трохвугольнік жыве ў хатцы з вялікім акном і нізкім дахам.
3) 3 трох хатак засталася толькі адна (1). 3 трох фігур застаўся квадрат. Значыць, квадрат жыве ў хатцы з высокім дахам і маленькім акном.
Адказы можна запісваць двума спосабамі:
а) схематычна - насупраць кожнай з фігур дзеці малююць хаткі з адпаведнымі дахамі і вокнамі;
б) указваючы нумары хатак (3, 2, 1).
Новыя варыянты гэтай жа гульні можна атрымаць шляхам змянення ўмовы задання:
1) замест ,О, узяць іншыя геаметрычныя фігуры, персанажаў казак, звяроў, імёны дзяцей, лікі, літары і г. д.;
2) замест трох "жыхароў" ,О, - узяць чатыры (магчыма і больш, але гэта ўжо надае заданню грувасткі выгляд);
3) у якасці прымет хатак можна браць, напрыклад, колер дахаў і форму акенцаў, вышыню хатак і наяўнасць у іх комінаў, форму дахаў і форму акенцаў і інш.;
4) вар'іраваць змест зыходных суджэнняў, на падставе якіх адшукваюцца адпаведныя хаткі.
Укладанне тых жа лагічных дзеянняў - пошуку лагічнага вываду з зыходных суджэнняў - у новы сюжэт прыводзіць да паяўлення новых гульняў. Напрыклад: "Дапамажы Дзеду Марозу", "Звяры - мастакі", "Парашутысты", "Цыркавое прадстаўленне".
Вар'іраванне ўмовы заданняў дазваляе праводзіць гульню дастаткова многа разоў для фарміравання трывалага ўмення рабіць лагічныя вывады з дадзеных суджэнняў.
Гульня "Дапамажы Дзеду Марозу"
Набліжаецца Новы год, і ў Дзеда Мароза вельмі шмат турбот, бо не можа ён пакінуць без падарункаў нікога са сваіх маленькіх сяброў. Сёння дзядуля падрыхтаваў для Колі, Галі і Петрыка такія падарункі: чырвоны паравоз, чырвоны мяч і драўлянага каня. Для Колі і Галі ён прызначыў не мяч, для Петрыка і Галі - цацкі чырвонага колеру. Дапамажы Дзеду Марозу размеркаваць падарункі.
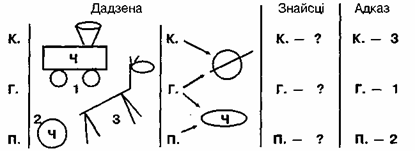
Гульня "Звяры-мастакі"
Мастакі Вавёрка, Мядзведзь, Лісіца і Бабёр падрыхтавалі да выставы свае малюнкі. Усе малюнкі былі розныя. Але былі ў мастакоў толькі дзве фарбы - чырвоная і карычневая, Кожны намаляваў або грыб, або елку. Вавёрка і лісіца выкарыстоўвалі чырвоную фарбу Лісіца і Бабёр намалявалі негрыбы. Што намаляваў кожны з мастакоў?
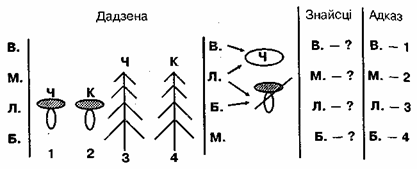
Гульня "Парашутысты"
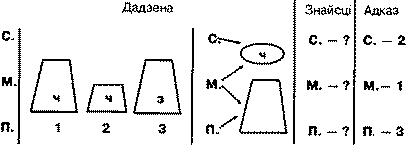
У спаборніцтве парашутыстаў удзельнічаюць Матылёк, Верабей, Заяц і Крот. Кожны з іх павінен прызямліцца дакладна на сваю пляцоўку. Пляцоўкі розныя: маленькая круглая, вялікая квадратная, маленькая прамавугольная і вялікая трохвугольная. Матылёк і Верабей павінны апусціцца на маленькія пляцоўкі, а Заяц і Верабей на чатырохвугольныя. Куды павінен прызямліцца кожны з парашутыстаў?
Гульня "Цыркавое прадстаўленне"
У цыркавым нумары ўдзельнічаюць Сабака, Малпа і Певень. На арэне для кожнага з іх паставілі тумбы: высокую чырвоную, нізкую чырвоную і высокую зялёную. Сабаку і Малпе адведзены чырвоныя тумбы, а Малпе і Пеўню - высокія. Хто на якой тумбе павінен сядзець?
Фарміраванне ўмення рабіць лагічныя вывады мае на мэце і некаторыя так званыя нестандартныя задачы (на размеркаванне), якія ў дастатковай колькасці прапануюцца ў падручніках матэматыкі пад рэдакцыяй А. А. Столяра [12, с.12 № 4, с. 23 № 6, с. 30 № 4, с. 42 № 4 і г. д.; 13, с. 47 № 75, с. 80 № 252, с. 90 № 305, с. 102 № 367 і г. д.] У якасці прыкладу прапануем арганізацыю работы ў час урока над задачай № 367 [13, с. 102],
"У Марыны, Каці, Соні, Ніны, Лізы і Тані былі два сабакі і чатыры кошкі. У Соні і Лізы былі аднолькавыя жывёлы, у Лізы і Марыны - розныя, у Каці і Соні - аднолькавыя, у Соні і Ніны - розныя. У каго была кошка, а ў каго быў сабака?"
Асэнсаванне зместу задачы
- Колькі было дзяўчынак? (6.)
- Як іх звалі? Запішам імёны дзяўчынак толькі першымі літарамі - М., К., С., Н., Л., Т.
- Колькі было сабак (2.)
- Колькі кошак? (4.)
- Колькі жывёл усяго? (6.)
- Было 6 дзяўчынак і 6 жывёл - у кожнай дзяўчынкі па адной жывёле. Аб чым трэба даведацца ў задачы? (У каго была кошка, а ў каго быў сабака?)
Пошук рашэння і выкананне задачы
- Што ў задачы вядома аб Соні і Лізе? (У іх аднолькавыя жывёлы.)
- Якія гэта могуць быць жывёлы? (Або сабака, або кошка.)
- Замест "кошка", "сабака" будзем запісваць маленькія літары "к.", "с." пад імёнамі дзяўчынак. У першым радзе запішам пад імёнамі Соні і Лізы літару "к.". Што гэта азначае? (У Соні кошка і ў Лізы таксама
кошка.)
- Што яшчэ вядома ў задачы? (У Лізы і Марыны розныя жывёлы.)
- Разважайце. (Вядома, што ў Лізы і Марыны розныя жывёлы. У Лізы кошка. Значыць, у Марыны сабака.)
- Як гэта запішам? (Пад літарай "М." напішам літару "с.".)
- Што гаворыцца ў задачы далей? (У Каці і Соні аднолькавыя
жывёлы.)
- Разважайце. (Вядома, што ў Соні і Каці аднолькавыя жывёлы.
.У Соні кошка. Значыць, у Каці таксама кошка.)
- Чытайце задачу далей і разважайце. (Вядома, што ў Соні і Ніны розныя жывёлы. У Соні кошка. Значыць, у Ніны - сабака. Напішам "с." Пад літарай "Н.". Засталася толькі адна кошка. Значыць, у Тані была кошка.) Вось які малюнак у нас атрымаўся.
М. К. С. Н. Л. Т.
с. к. к. с. к. к.
- Адкажыце на пытанне задачы.
Рашэнне дадзенай задачы ўяўляе паслядоўнасць лагічных вывадаў з умовы. Паўтарэнне рашэння садзейнічае не толькі лепшаму асэнсаванню спосабу рашэння аналагічных задач, але і замацаванню ўмення рабіць вывады.
Мы разгледзелі агульны падыход да рашэння задач такога тыпу. У дадзенай задачы ўважлівы аналіз умовы прыводзіць да больш
рацыянальнага рашэння.
- У каго з дзяўчынак былі аднолькавыя жывёлы? (У Соні і Лізы, у Каці і Соні. Значыць, аднолькавыя жывёлы былі ў трох дзяўчынак: Соні, Лізы і Каці. Сабак толькі два. Значыць, у гэтых дзяўчынак былі
кошкі).
- У каго з дзяўчынак былі розныя жывёлы? (У Лізы і Марыны розныя. У Соні і Ніны розныя, У Лізы кошка, значыць, у Марыны сабака. У Соні кошка, значыць, у Ніны сабака. Засталася яшчіэ адна кошка і дзяўчынка Таня. Значыць, у Тані кошка).
II. Мэта - навучанне абгрунтаванню праўдзівасці
суджэнняў (падбору адпаведных аргументаў
для доказу праўдзівасці суджэнняў)
Гульня "У краіне Нетакай"
- Сёння мы з вамі адправімся ў краіну пад назвай Нетакай. Чаму яе называюць менавіта так? Як вы думаеце?
Настаўнік выслухоўвае меркаванні дзяцей і тлумачыць, што клас трапіў у краіну зусім не такую, як наша. Яе рэчаіснасць адрозніваецца ад той, у якой жывём мы.
- Многія прадметы ў гэтай краіне характарызуюць зусім не так, як у нас, таму што ў Нетакаі дзейнічае такі закон фарбаў:
"Усё белае лічыць чорным, чорнае - сінім, сіняе - жоўтым, жоўтае - зялёным, зялёнае - чырвоным, а чырвонае - белым. Усе астатнія колеры пакінуць без змяненняў".
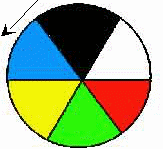
Можна прапанаваць дзецям выканаць пэўнае заданне (рашыць задачу, прыклады, знайсці памылку і інш.), каб апынуцца ў Нетакаі. Усе далейшыя заданні датычацца апісання новых прымет, якія набываюць у Нетакаі добра вядомыя аб'екты. Свой адказ вучні абавязкова павінны абгрунтоўваць, г. зн. даказваць, спасылаючыся толькі на законы, якія дзейнічаюць у Нетакаі. Напрыклад:
- Як выглядае рамонак у Нетакаі? (Зялёная сярэдзіна і чорныя пялёсткі, таму што ў Нетакаі жоўтае лічыцца зялёным, а белае - чорным.)
- Ці будуць у апісанні нетакайскага васілька словы "жоўты", "чырвоны"? (Так. Жоўтыя пялёсткі і чырвонае сцябло, таму што сіняе ў Нетакаі лічыцца жоўтым, а зялёнае - чырвоным.)
- Ці ёсць у Нетакаі чырвоныя ружы? (Няма, таму што, каб сказаць "чырвоная ружа", нетакаец павінен убачыць нашу ружу з зялёнымі пялёсткамі, а такіх руж у нас няма.)
- Ці ёсць у Нетакаі чорныя ружы? (Так, таму што чорнай у Нетакаі назавуць ружу, якая ў нас з'яўляецца белай. А белыя ружы ў нас ёсць.)
- Як у Нетакаі будзе выглядаць карычневая кашуля Кастуся? (Кашуля застанецца карычневай, таму што карычневы колер не змяняецца.)
Можна папрасіць дзяцей уявіць і расказаць, як будзе выглядаць у Нетакаі хто-небудзь з вучняў класа. Наогул, для характарыстыкі можна браць любыя аб'екты: танкі (стануць чырвонымі), гарматы (стануць сінімі), дрэвы (?), неба (?), сонца (?), розныя школьныя прылады, г. зн. усё, што акружае дзяцей, да чаго яны маюць цікавасць. Слоўнае "маляванне" можна замяніць сапраўдным маляваннем.
Відавочна, што ў прапанаваным варыянце гульня "У краіне Нетакай" можа мець шматразовае выкарыстанне. Іншыя варыянты яе можна атрымаць праз "выданне" новых законаў, якія могуць дзейнічаць у Нетакаі асобна або ў спалучэнні з раней "выдадзенымі" законамі.
Напрыклад, закон памераў:
"Усё, што ў нас вышэйшае (даўжэйшае) за 2 м, называюць маленькім, а што ў нас ніжэйшае (карацейшае) за 2 м, называюць вялікім".
- Вялікімі ці маленькімі называюць у Нетакаі нашы палявыя кветкі? (Вялікімі, таму што ў нас яны не большыя за 2 м.)
- Аб старым дрэве ці аб кусціку нетакайцы скажуць "вышэйшы"? (Аб кусціку, таму што ў Нетакаі кусцікі называюць вялікімі, бо яны ў нас ніжэйшыя за 2 м, а дрэвы - маленькімі, бо яны ў нас вышэйшыя за 2 м.)
- Хто ў Нетакаі вышэйшы: баскетбаліст ростам 2 м 5 см ці наш Петрык? (Петрык, таму што яго рост меншы за 2 м і ён лічыцца вялікім, а ў баскетбаліста рост большы за 2 м і ён лічыцца маленькім.)
Галоўнае, каб дзеці не проста выказвалі свае суджэнні, а і абавязкова знаходзілі для іх абгрунтаванне, карыстаючыся пры гэтым толькі дапушчальнымі ў краіне Нетакай умовамі (законамі краіны) і не спасылаючыся ні на якія іншыя веды або рэальныя ўяўленні.
У падручніках матэматыкі пад рэдакцыяй А.А. Столяра сустракаюцца задачы. (назавём іх імавернаснымі), у якіх адказ на пытанне патрабуе лагічнага абгрунтавання [11, частка 1, с. 27, 28; 13, с. 59 № 141, с. 85 № 279, с. 156 № 145, с. 190 № 42 і інш.].
Разгледзім рашэнне задачы №141 [13, с. 59].
"У мяшочку ляжаць 4 чырвоныя і 4 сінія шарыкі. Колькі шарыкаў трэба выняць з мяшочка наўгад, каб сярод іх:
а) быў 1 чырвоны шарык;
б) былі 2 шарыкі рознага колеру;
в) не было шарыкаў рознага колеру;
г) не было ніводнага чырвонага шарыка?"
Рашэнне
а) Калі выняць 1 шарык, то ён можа аказацца сінім. Значыць, лік 1 не падыходзіць.
Калі выняць 2 шарыкі, то можа здарыцца, што:
я
 ны абодва чырвоныя –
ны абодва чырвоныя – або 1 чырвоны і 1 сіні –
або 2 сінія
Значыць, лік 2 не падыходзіць.
Калі выняць 3 шарыкі, то можа здарыцца, што:
у
 се 3 чырвоныя -
се 3 чырвоныя - або 2 чырвоныя і 1 сіні –
або 1 чырвоны і 2 сінія –
або ўсе 3 сінія -
Значыць, лік 3 не падыходзіць.
Калі выняць 4 шарыкі, то можа здарыцца, што:
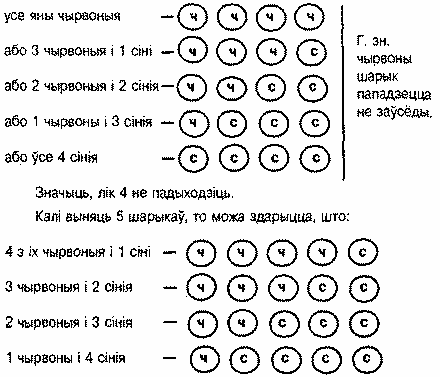
Нічога іншага быць не можа. У кожным выпадку абавязкова ёсць чырвоны шарык. Значыць, лік 5 падыходзіць.
Адказ. Каб 1 шарык быў чырвоным, трэба выняць 5 шарыкаў.
Аналіз кожнага з выкананых крокаў пошуку адказу ў папярэднім пункце прыводзіць да адказу і на ўсе наступныя пытанні.
Адказы. б) Каб былі 2 шарыкі рознага колеру, трэба выняць 5 шарыкаў; в) каб не было шарыкаў рознага колеру, трэба выняць 1 шарык; г) немагчыма, каб не было ніводнага чырвонага шарыка, таму што яны ў мяшочку ёсць, а значыць, заўсёды ёсць магчымасць дастаць чырвоны шарык.
Пасля набыцця пэўнага вопыту ў рашэнні імавернасных задач колькасць спроб можна скараціць, адразу адкідваючы тыя з іх, якія ўжо на першых кроках не адпавядаюць патрабаванню задачы. Але адзначым, што пры рашэнні такіх задач правільны адказ трэба не адгадаць, а лагічна абгрунтаваць. Уменне даць разважанне ў поўнай форме сведчыць аб свядомасці выканання рашэння. А трэніроўка ў абгрунтаванні суджэнняў садзейнічае фарміраванню матэматычнага стылю мыслення.
Імавернасныя задачы настаўнік па аналогіі можа складаць і самастойна. Пры гэтым пажадана вар'іраваць: 1) агульнай колькасцю шарыкаў у мяшочку; 2) суадносінамі паміж колькасцю шарыкаў двух розных колераў (пароўну, непароўну - розныя выпадкі); 3) колерам шарыкаў; 4) аднароднымі прадметамі, што кладуць у мяшочак (кубікі, гузікі, фасоліны і інш.).
Да прадметаў у "цудоўным" мяшочку прад'яўляецца адзінае патрабаванне - яны павінны мець толькі адну адметную рысу, якую нельга распазнаць навобмацак.
Прапедэўтычную ролю могуць выконваць не толькі спецыяльныя, нетрадыцыйныя для пачатковага навучання заданні, але і звычайныя, праграмныя, калі ў лік задач навучання ўключыць выхаванне ў дзяцей патрэбнасці ў доказе, г. зн. звычкі абгрунтоўваць свае суджэнні, меркаванні. Прычым не толькі на ўроках матэматыкі, а ўвогуле пры засваенні разнастайных ведаў і ўменняў, якія набываюцца ў школе. Для развіцця лагічнага мыслення і выхавання імкнення да доказу ёсць адпаведныя спрыяльныя сітуацыі на кожным уроку. Прывядзём некалькі прыкладаў разгорнутых адказаў вучняў, дзе не толькі фармулюецца некаторае сцверджанне, але і даецца дэдуктыўнае абгрунтаванне яго праўдзівасці.
"Гэта прамавугольнік, таму што ў ім чатыры вуглы і ўсе яны прамыя".
"7 • 1 = 7, таму што пры множанні любога ліку на адзін атрымліваецца той жа самы лік".
"Задача рашаецца адыманнем, таму што, каб даведацца, на колькі адзін лік большы або меншы за другі, трэба ад большага ліку адняць меншы".
"3 м 4 см = 304 см, таму што 1 м =100 см, значыць, 3 м = = 300 см, а 3 м 4 см = 300 см + 4 см = 304 см".
У гэтых дэдуктыўных разважаннях дзеці спасылаюцца на вядомыя ім азначэнні і правілы, г.зн. падводзяць прыватны выпадак пад агульнае сцверджанне.
Вельмі часта дэдуктыўныя вывады маюць няпоўную форму, калі некаторыя пасылкі (часцей вялікая) апускаюцца: яны не вымаўляюцца ўслых, а толькі маюцца на ўвазе. Прывядзём адпаведныя прыклады.
"96 : 16 = 6, таму што 6 • 16 = 96".
Тут адсутнічае вялікая пасылка - азначэнне дзялення: "Падзяліць адзін лік на другі - гэта значыць знайсці такі трэці лік, які пры множанні на другі лік дае першы лік". Але ў пачатковым курсе матэматыкі гэта азначэнне і не ўводзіцца. Уяўленне аб узаемасувязі дзялення з множаннем дзеці атрымліваюць праз аператыўныя правілы знаходжання дзялімага і праверкі дзялення множаннем. Таму ў дадзеным выпадку адсутнасць вялікай пасылкі з'яўляецца зразумелай. Інтуітыўна яна маецца на ўвазе.
Іншае становішча ў наступных выпадках.
1. "38 : 2 = ? 38 - гэта сума лікаў 20 і 18. Зручна падзяліць кожнае складаемае асобна і атрыманыя вынікі скласці: 20 : 2 = 10, 18 : 2 = = 9, 10 + 9 = 19. Значыць, 38 : 2 = 19".
У поўнай форме дадзенае разважанне мае выгляд: "Каб падзяліць суму на лік, можна падзяліць на гэты лік кожнае складаемае і атрыманыя вынікі скласці. 38 - гэта сума лікаў 20 і 18. Значыць, можна кожнае складаемае падзяліць на 2
(20 : 2 = 10, 18 : 2 = 9) і атрыманыя вынікі скласці (10 + 9 = 19). 38 : 2 = 19".
Вялікая пасылка дадзенага разважання добра вядома вучням як правіла дзялення сумы на лік. У такіх выпадках вымаўленне вялікай пасылкі ўслых не толькі стварае ўмовы для трэніроўкі ў разважаннях па правілах вываду, але ў той жа час забяспечвае свядомасць засваення вылічальнага прыёму. Такія лагічныя практыкаванні асабліва карысныя на этапе першаснага замацавання прыёмаў вылічэнняў.
2. "54 - 16 = 32. 32 + 16 = 48. Значыць, адыманне выканана няправільна".
Поўная форма адпаведнага разважання мае выгляд: "Калі адыманне выканана правільна, то сума рознасці і адымаемага роўна памяншаемаму. 54 - памяншаемае, 16 - адымаемае, 32 - рознасць. 32 + 16 = 48. 48 = 54. Значыць, адыманне выканана няправільна".
У школьнай практыцы часта можна назіраць фармальны падыход вучняў да праверкі. Яе зводзяць да маніпуліравання лікамі па пэўнай схеме. Прычына гэтай распаўсюджанай з'явы ў тым, што ў свядомасці дзяцей лагічныя і вылічальнуя аперацыі існуюць кожная сама па сабе. Асэнсаваць іх непарыўную ўзаемасувязь і абудзіць крытычнасць мыслення дазваляе менавіта разважанне ў поўнай форме (з вымаўленнем вялікай пасылкі). У працэсе адпаведнай трэніроўкі фарміруецца паўнацэннае ўменне выконваць самаправерку.
3 прыведзеных прыкладаў бачна, што нават традыцыйны змест пачатковай матэматычнай адукацыі дае вучням магчымасць сістэматычна практыкавацца ў дэдуктыўных разважаннях. Яны яшчэ вельмі простыя - складаюцца толькі з аднаго вываду, але непасрэдна садзейнічаюць як павышэнню лагічнай граматнасці вучняў, так і свядомаму засваенню вучэбнага матэрыялу.
