Geum.ru

Теория паросочетаний. Теорема Холла. Задача о назначениях. Лекция

Вид материалаЗадача

Содержание


Терема Холла.
Размер минимального контрольного множества равен размеру максимального паросочетания.
Список литературы по теме лекции, рекомендованной студентам
Подобный материал:
Теория паросочетаний. Теорема Холла. Задача о назначениях.

Лекция

Ключевым в сегодняшней лекции будет понятие двудольного графа, поэтому начнем с него.


Неориентированный граф называется двудольным, если множество его вершин V можно разбить на два непересекающихся подмножества V1 и V2, такие что не существует ребер, соединяющих две вершины из V1 и не существует ребер соединяющих две вершины из V2. То есть это означает, что все ребра соединяют вершины из V1с какими-то вершинами из V2, Пример двудольного графа.




Как видно из определения и примера, двудольные графы позволяют представить отношения между двумя классами объектов. Например, это могут быть работники и технологические операции. В это м случае ребро между определенным работником и операцией означает, что данный работник может выполнить эту операцию.

Следующий пример. Аудитории и учебные занятия. Ребро проводится в том случае, если данное занятие можно проводить в этой аудитории.

Третьим примером могут быть учебные дисциплины и преподаватели, которые могут вести занятия по этим дисциплинам.

Но, конечно же, эти графы не имеет смысла рисовать только для того, чтобы наглядно продемонстрировать указанные отношения. Каждый из этих примеров дает нам оптимизационную задачу.

Так, в примере с работниками и технологическими операциями может быть задана длительность каждой операции. Тогда естественно возникает задача распределения операций между работниками с целью минимизации общего времени выполнения работ.

Для примера с аудиториями и занятиями можно поставить задачу распределения занятий по аудиториям с целью равномерной загрузки аудиторий. (Если эту задачу удастся решить, то, например, проректору по учебной работе можно будет представить список особо загруженных и незагруженных аудиторий).

В третьем примере может быть задана учебная нагрузка по каждой дисциплине. Тогда задача программы — распределить учебную нагрузку по преподавателям, так, чтобы никто не вел занятий больше нормы.


Для того, чтобы понять идею решения подобных задач, мы рассмотрим другую (классическую) задачу, которая дала название данному разделу теории графов. Это так называемая задача о свадьбах.

В одной изолированной от внешнего мира общине есть N юношей и столько же девушек. Для каждого юноши известен список девушек, которые нравятся этому юноше. Староста общины хочет поженить всех юношей и девушек, однако юноши наотрез отказываются жениться на девушках, которые им не нравятся. Определить, сможет ли староста добиться своей цели.

Очевидно, что в терминах теории графов это означает выбрать из множества ребер R подмножество R`, состоящее из N ребер, таких что никакая вершина не встречается в записи ребер R` дважды.


Как мы уже делали раньше, изобретем алгоритм для решения этой задачи, и этот алгоритм поможет нам найти некоторые важные свойства этой задачи. На самом деле эта задача решается достаточно просто. Дело в том что ее можно свести к уже известной нам задаче о потоке. Для этого к данному двудольному графу необходимо добавить две вершины, так как это показано на рисунке


























Как видно из рисунка каждую из добавленных вершин мы соединили одним ребром с каждой вершиной одной доли. Теперь припишем всем вершинам (в том числе и добавленным) пропускную способность равную 1, и запустим алгоритм нахождения максимального потока от первой добавленной вершины ко второй. Для алгоритма потока нам требуется, чтобы граф был ориентированный. Мы добавим ориентацию всем ребрам так, чтобы на рисунке все стрелочки вели от левых вершин к правым.


Поскольку минимальное приращение потока равно 1, алгоритм нахождения максимального потока либо заполнит некоторое ребро потоком в 1, либо оставит его незаполненным. Тогда понятно, что ни из какой вершины первой доли не смогут выйти два заполненных ребра (ведь к этим вершинам приходит поток равный 1). Но и в вершины второй доли не сможет войти два заполненных ребра (ведь из этих вершин может выйти поток лишь равный 1). Тем самым, заполненные ребра между вершинами двух долей и дадут нам максимальное паросочетание.

С другой стороны если максимальное паросочетание существует, то заполнив его ребра потоком в 1, а также заполнив все добавленные ребра, мы получим поток размера N. Понятно, что это максимально возможное значение потока.

Тем самым мы доказали, что алгоритм поиска максимального потока решает задачу о максимальном паросочетании.

Заметим, что данный случай использования алгоритма позволяет существенно упростить его. Поэтому можно записать более короткое и простое, чем для задачи о потоке решение. Однако, мы пока не будем делать этого, поскольку далее нам потребуется небольшая модификация этого алгоритма.

Пока же мы можем доказать следующую теорему.


Терема Холла.

Максимальное паросочетание в двудольном графе существует тогда и только тогда, когда мощность всякого подмножества вершин первой доли V’ меньше или равна мощности множества вершин второй доли инцидентных вершинам V’.

Применительно к нашей задаче можно сформулировать это так. Максимальное количество свадеб возможно, если для любой группы юношей количество девушек, которые нравятся хотя бы одному из юношей, больше чем количество юношей.

Доказательство

В одну сторону доказательство очевидно Действительно, если для некоторого V’ количество инцидентных вершин во второй доле меньше чем вершин в V’, то какой-нибудь вершине из V’ в любом случае не найдется пары.


Докажем теорему в другую сторону. Вспомним алгоритм насыщения потока. Пусть у нас есть некоторое паросочетание, которое пока не является максимальным. Запустим алгоритм насыщения с вершины которая не входит в паросочетание. При поиске ненасыщенного пути алгоритм будет двигаться от вершин первой доли ко второй и тут же возвращаться к вершинам первой доли. Тем самым если алгоритм будет помечать пройденные вершины обеих долей, то для каждой вершины второй доли он пометит хотя бы одну вершину первой доли, плюс ту вершину, с которой он начинает. Таким образом, если алгоритму не удастся произвести насыщение пути, то есть добавить новую вершину в паросочетание, он найдет такое подмножество вершин V’, что суммарное количество вершин инцидентных V’ будет меньше, чем вершин из V’, что доказывает теорему.


Для решения дальнейших задач нам потребуется еще одно понятие: контрольное множество. Будем говорить что ребро (a,b) контролируется вершиной a, либо вершиной b. В таком случае можно поставить следующую задачу: в заданном двудольном графе построить минимальное контрольное множество, то есть минимальное множество вершин, которые контролируют все ребра.

Оказывается контрольное множество и паросочетания обладают свойством, которое мы сформулируем в виде теоремы.

Теорема. Размер минимального контрольного множества равен размеру максимального паросочетания.

Во-первых, размер любого паросочетания не превосходит размера любого контрольного множества, так как каждое ребро из паросочетания должно контролироваться своей вершиной.

Далее. Если в графе есть максимальное паросочетание, то в качестве контрольного множества возьмем все вершины первой доли. Очевидно, размеры контрольного множества и паросочетания совпадут.

Теперь пусть в графе нет максимального паросочетания, тогда для него не полнено условие теоремы Холла. Обозначим за V’1 минимальное подмножество вершин первой доли , для которых не выполнено условие теоремы Холла, а за V’2 множество вершин второй доли инцидентных вершинам изV’1 Количество вершин в паросочетании будет равно мощности множества V’2 Тогда добавим в контрольное множество все вершины из V’2 Они будут полностью контролировать двудольный подграф из вершин V’1 и V’2,и их количество совпадет с размером паросочетания в этом подграфе. Далее будем рассматривать двудольный подграф, состоящий из вершин V1 \V’1 и V’2 \V’2 и повторим для него предшествующие рассуждения. Тем самым мы построим паросочетание равное размеру контролирующего множества.

Теорема доказана


С помощью теории паросочетаний мы сможем решить еще одну очень интересную задачу — задачу о назначениях.

Сформулируем ее в следующем виде: в сельской местности работает N передвижных магазинов. По завершении работы все они должны переехать из тех населенных пунктов, где они находятся в другие. Обозначим за Aij расстояние от i-того исходного населенного пункта к j-тому населенному пункту назначения. Составить план перемещения передвижных магазинов так, чтобы суммарное пройденное расстояние оказалось минимальным.


Очевидно, что эту задачу можно представить в следующей форме: Задана квадратная матрица из натуральных чисел размера N на N. Выбрать в ней N ячеек так, чтобы в каждой строке и в каждом столбце была ровно одна выбранная ячейка и сумма значений в этих ячейках была минимально возможной.


Как можно решить эту задачу? Во-первых отметим, что если мы отнимем от всех ячеек некоторой строки произвольное число K, то сумма любого набора ячеек уменьшится на K, тем самым эта операция не влияет на выбор ячеек. То же самое можно сказать и о произвольном столбце. Тем самым можно указать первый шаг алгоритма решения этой задачи. Необходимо выбрать минимальное значение в каждой строке и уменьшить все элементы строки на это значение. Аналогичную операцию надо проделать со столбцами.


Что можно сделать дальше? Составим двудольный граф с N вершинами в каждой доле и проведем ребро от i-той вершины первой доли к j-той вершине второй доли в том случае если после преобразований ячейка Aij равна нулю. Попытаемся найти максимальное паросочетание в этом графе. Если это удалось сделать, то именно это паросочетание и определит выбранные ячейки. Сумма в них будет равна 0 и это минимально возможное значение.

Если же максимального паросочетания нет, то возьмем минимальное контролирующее множество вершин. Вычеркнем из матрицы все строки соответствующие элементам контролирующего множества первой доли и все столбцы соответствующие контролирующему множеству из второй доли. По определению контролирующего множества полученная матрица не будет содержать нулей. Выберем в этой матрице минимальный элемент K. После этого прибавим K ко всем ячейкам из вычеркнутых строк и отнимем от всех ячеек невычеркнутых столбцов. В результате такого преобразования в матрице не появится отрицательных чисел.

Кроме того вычеркнутых строк меньше чем невычеркнутых столбцов, поскольку паросочетание не было максимальным. Тем самым мы уменьшили сумму всех элементов матрицы.

В результате описанных преобразований сумма элементов матрицы все время уменьшается, следовательно описанный процесс когда-нибудь закончится. Он может закончится только с нахождением максимального паросочетания, что решит задачу.

Рассмотрим пример. Исходные населенные пункты обозначены буквами, пункты назначения — цифрами.
1
2
3
4
5
6
7
8

A
32
11
19
18
44
65
23
18

B
41
54
23
19
87
16
25
33

C
47
34
41
26
15
47
29
52

D
73
14
10
0
12
29
33
50

E
37
33
18
29
26
26
41
84

F
72
61
38
96
26
14
55
47

G
38
17
26
49
28
91
97
24

H
32
52
67
71
33
56
54
22


Найдем в каждой строке матрицы минимальное значение и вычтем его из всех ячеек строки
1
2
3
4
5
6
7
8

A
21
0
8
7
33
54
12
7

B
25
38
7
3
71
0
9
17

C
32
19
26
11
0
32
14
37

D
73
14
10
0
12
29
33
50

E
19
15
0
11
8
8
23
66

F
58
47
24
82
12
0
41
33

G
21
0
9
32
11
74
80
7

H
10
30
45
49
11
34
32
0

В первом и седьмом столбцах минимальный элемент больше нуля, поэтому вычтем его
1
2
3
4
5
6
7
8

A
11
0
8
7
33
54
3
7

B
15
38
7
3
71
0
0
17

C
22
19
26
11
0
32
5
37

D
63
14
10
0
12
29
24
50

E
9
15
0
11
8
8
14
66

F
48
47
24
82
12
0
32
33

G
11
0
9
32
11
74
71
7

H
0
30
45
49
11
34
23
0


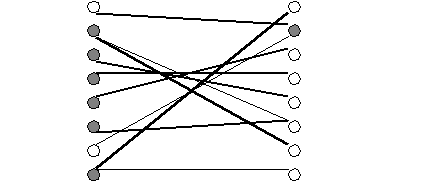
Строим двудольный граф, находим в нем максимальное паросочетание и контролирующее множество

A 1

B 2

C 3

D 4

E 5

F 6

G 7

H 8

Паросочетание не максимально. Пометим все не контролируемые строки и столбцы
1
2
3
4
5
6
7
8

A
11
0
8
7
33
54
3
7

B
15
38
7
3
71
0
0
17

C
22
19
26
11
0
32
5
37

D
63
14
10
0
12
29
24
50

E
9
15
0
11
8
8
14
66

F
48
47
24
82
12
0
32
33

G
11
0
9
32
11
74
71
7

H
0
30
45
49
11
34
23
0

Минимальный элемент в выделенной части таблицы — 3.

Прибавляем 3 ко всем строкам, кроме A и G и отнимаем от всех столбцов, кроме 2. Получим матрицу
1
2
3
4
5
6
7
8

A
8
0
5
4
30
51
0
4

B
15
41
7
3
71
0
0
17

C
22
22
26
11
0
32
5
37

D
63
17
10
0
12
29
24
50

E
9
18
0
11
8
8
14
66

F
48
50
24
82
12
0
32
33

G
8
0
6
29
8
71
68
4

H
0
33
45
49
11
34
23
0

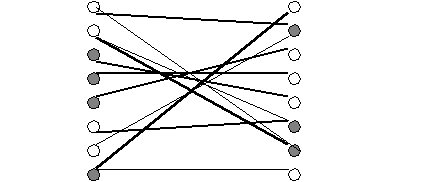
Вновь построим граф и паросочетание.

A 1

B 2

C 3

D 4

E 5

F 6

G 7

H 8

Паросочетание не максимально. Пометим все не контролируемые строки и столбцы
1
2
3
4
5
6
7
8

A
8
0
5
4
30
51
0
4

B
15
41
7
3
71
0
0
17

C
22
22
26
11
0
32
5
37

D
63
17
10
0
12
29
24
50

E
9
18
0
11
8
8
14
66

F
48
50
24
82
12
0
32
33

G
8
0
6
29
8
71
68
4

H
0
33
45
49
11
34
23
0

Минимальный элемент в выделенной части 3. Добавим его к строкам C, D, E, H и вычтем из столбцов 1, 3, 4, 5, 8. В результате получим
1
2
3
4
5
6
7
8

A
5
0
2
1
27
51
0
1

B
12
41
4
0
68
0
0
14

C
22
25
26
11
0
35
8
37

D
63
20
10
0
12
32
27
50

E
9
21
0
11
8
11
17
66

F
45
50
21
79
9
0
32
30

G
5
0
3
26
5
71
68
1

H
0
36
45
49
11
37
26
0

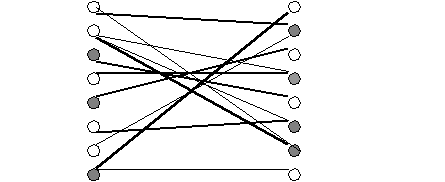
Опять построим граф и паросочетание.

A 1

B 2

C 3

D 4

E 5

F 6

G 7

H 8

Паросочетание не максимально. Пометим все не контролируемые строки и столбцы
1
2
3
4
5
6
7
8

A
5
0
2
1
27
51
0
1

B
12
41
4
0
68
0
0
14

C
22
25
26
11
0
35
8
37

D
63
20
10
0
12
32
27
50

E
9
21
0
11
8
11
17
66

F
45
50
21
79
9
0
32
30

G
5
0
3
26
5
71
68
1

H
0
36
45
49
11
37
26
0

Минимальный элемент — 1. Добавим его к строкам C, E, H и вычтем из столбцов 1,3, 5, 8. В результате получим
1
2
3
4
5
6
7
8

A
4
0
1
1
26
51
0
0

B
11
41
3
0
67
0
0
13

C
22
26
26
12
0
36
9
37

D
62
20
9
0
11
32
27
49

E
9
22
0
12
8
12
18
66

F
44
50
20
79
8
0
32
29

G
4
0
2
26
4
71
68
0

H
0
37
45
50
11
38
27
0

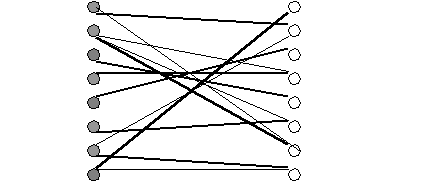
Строим граф и паросочетание.

A 1

B 2

C 3

D 4

E 5

F 6

G 7

H 8

Максимальное паросочетание есть и оно определяет наилучшее назначение. Это

(A,2),(B,7),(C,5),(D,4),(E,3),(F 6),(G,8) ,(H,1)


Список литературы по теме лекции, рекомендованной студентам


  1. Новиков Ф.А. Дискретная математика для программистов. — СПб.: Питер, 2001 г.
  2. Романовский И.В. Дискретный анализ. — СПб.: Невский диалект, 2000 г.


Основное содержание лекции можно найти в учебном пособии [2]. Стиль изложения при этом более похож на стиль учебника [1].

Список литературы по теме лекции

  1. Новиков Ф.А. Дискретная математика для программистов. — СПб.: Питер, 2001 г.
  2. Романовский И.В. Дискретный анализ. — СПб.: Невский диалект, 2000 г.
  3. Евстигнеев В.А. Применение теории графов в программировании. — М. Наука, 1985 г.



Задачи по программированию с Интернет источников




  1. www.topcoder.com
  2. acm.timus.ru
  3. algolist.manual.ru