Внастоящее время, задачи решаемые рэу все более усложняются, это ведет к усложнению конструкции рэу и требование к поставленным задачам также велики
| Вид материала | Задача |
СодержаниеВспомогательные и промежуточные параметры |
- Конспект лекций Москва гоу впо «рэу им. Г. В. Плеханова» 2011, 608.99kb.
- Литература: 1 Алексеев В. Ф. «Принципы конструирования и автоматизации проектирования, 597.13kb.
- Гармаев Булат Петрович, к ю. н., доцент кафедры экономического права и гражданско-правовых, 590.61kb.
- Информация об основных технико-экономических показателях по ООО «Управляющая компания, 25.42kb.
- Внастоящее время в мире повсеместно и во все более разрастающихся масштабах происходит, 373.75kb.
- Информация об основных технико-экономических показателях по ООО «ук рэу №11» городского, 104.6kb.
- Права сексуальных меньшинств в западных странах и в России, 404.86kb.
- Права сексуальных меньшинств в западных странах и в России: сравнительная характеристика, 407.09kb.
- Рабочая программа учебной дисциплины документоведение (название дисциплины), 703.88kb.
- Организация рекламной деятельности малого торгового предприятия и ее эффективность, 276.69kb.
Введение
В настоящее время, задачи решаемые РЭУ все более усложняются, это ведет к усложнению конструкции РЭУ и требование к поставленным задачам также велики. Одним из важнейших требований предъявляемой к РЭУ является точность выходных параметров.
Точность выходных параметров характеризует степень приближения его истинного значения к номинальному, при отклонении первичных параметров, соответствующих производственным погрешностям. Из всего многообразия методов решения этой задачи большой интерес представляют следующие методы: метод Монте-Карло (метод статических испытаний) и вероятностный метод.
Метод Монте-Карло использующий математическое моделирование, реализуют, как правило, на ЭВМ. Отечественный и зарубежный опыт показывают, применение ЭВМ для целей оценки точности выходных параметров способствует повышению технического уровня изделий, так как на ЭВМ можно смоделировать и просчитать большее число альтернативных вариантов и выбрать из множества вариантов наиболее лучший (оптимальный или близкий к оптимальному).
Вероятностный метод, а иначе расчетно-аналитический метод с учетом вероятностного рассеивания первичных параметров, решается с помощью аналитических методов.
1.Постановка задачи
- Исходные данные
Исходными данными для выполнения расчетов, согласно заданию на курсовое проектирование, являются:
1.РЭС – дифференциальный усилитель.
2.Электрическая принципиальная схема.
3.Математическая модель для выходного параметра (выходное напряжение)
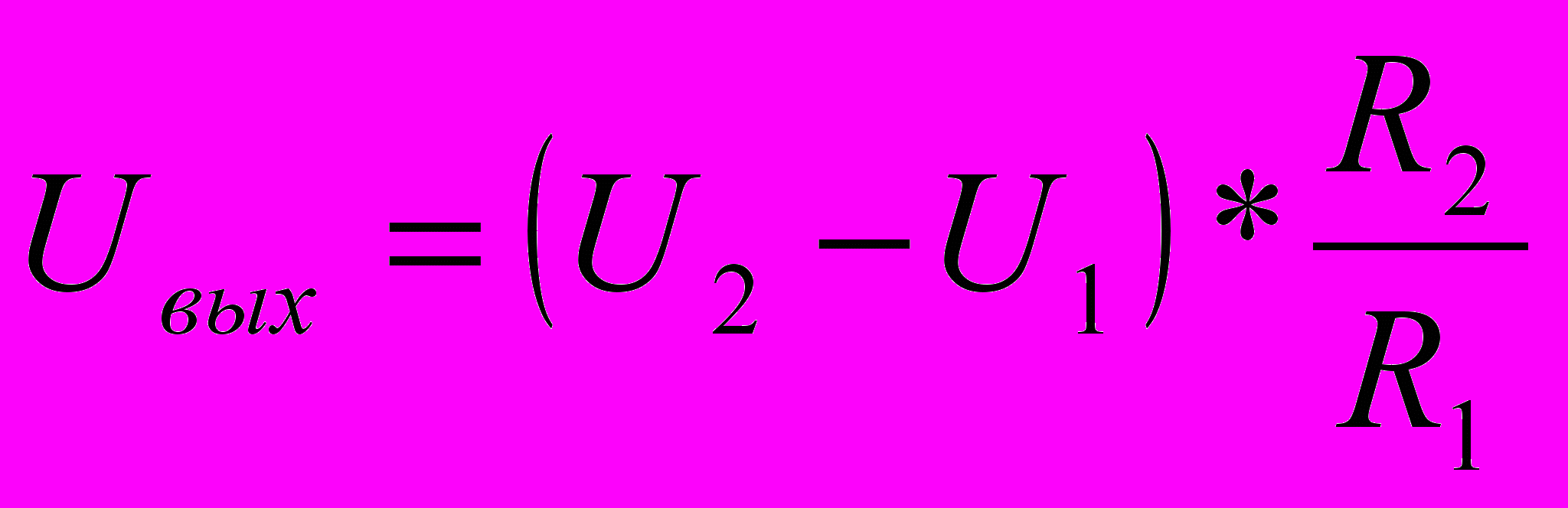(1.1)4.Сведения о первичных параметрах:
R1=3кОм10%;
R2=10кОм10%;
Исполнение резисторов - интегральное.
Микросхема DА1:140УД8.
U1=100мВ10%; U2=150мВ30% .
5.Диапазон рабочих температур +10…+45
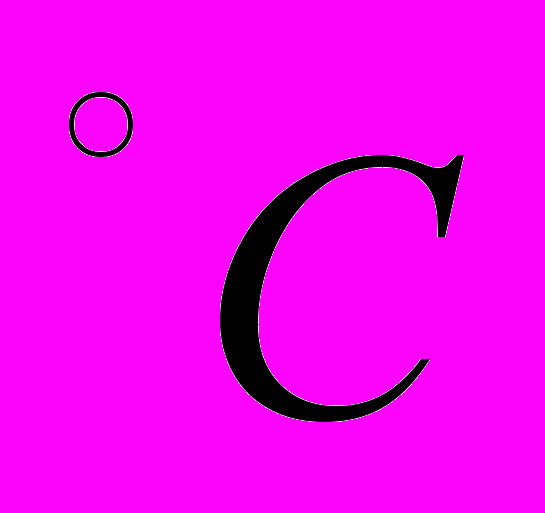. 6.Заданное время работы РЭС:10000 часов.
- Формулировка поставленной задачи
Из задания на курсовое проектирование для решения нашей задачи методом Монте-Карло и вероятностным методом известны все требуемые данные. В наших исходных данных есть параметры, которые не нужны для решения поставленной задачи: диапазон рабочих температур и заданное время работы РЭС. Не известный нам параметр – корреляция между резисторами. Для резисторов с интегральным исполнением корреляция положительная и лежит в диапазоне от 0.85 до 0.95 . Для нашей задачи возьмем корреляцию 0.9.
Исходя из допусков на первичные параметры, которые более десяти процентов, воспользуемся для решения задачи нормальным законом распределения первичных параметров.
В результате решения нашей задачи двумя методами мы получим значения выходного параметра (Uвых)-математическое ожидание и среднее квадратическое отклонение(СКО). Сравнив полученные результаты двумя методами, мы сможем сделать вывод о точности методов.
2.Краткое описание используемых методов
2.1.Метод Монте-Карло
Этот метод иначе называется методом статистических испытаний. С помощью этого метода можно оценить М(y)-математическое ожидание (среднее значение) выходного параметра и
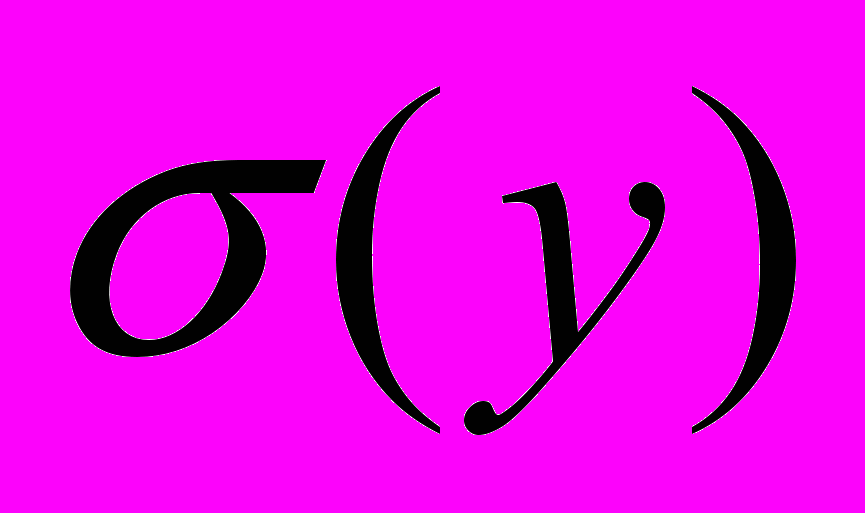-среднее квадратическое отклонение выходного параметра.Основу метода Монте-Карло составляет процесс получения случайных реализаций устройства или процесса. Каждая реализация описывается значением выходного параметра рассматриваемого устройства или процесса. Как правило, ей соответствует определенное сочетание первичных параметров и новое значение выходного параметра. Значения первичных параметров для той или иной реализации устанавливают не произвольно, а с учетом их вероятностного описания. Значения выходного параметра в каждой реализации определяются, как правило, новой комбинацией первичных параметров. Получив N реализаций устройства или процесса, можно сформировать ряд
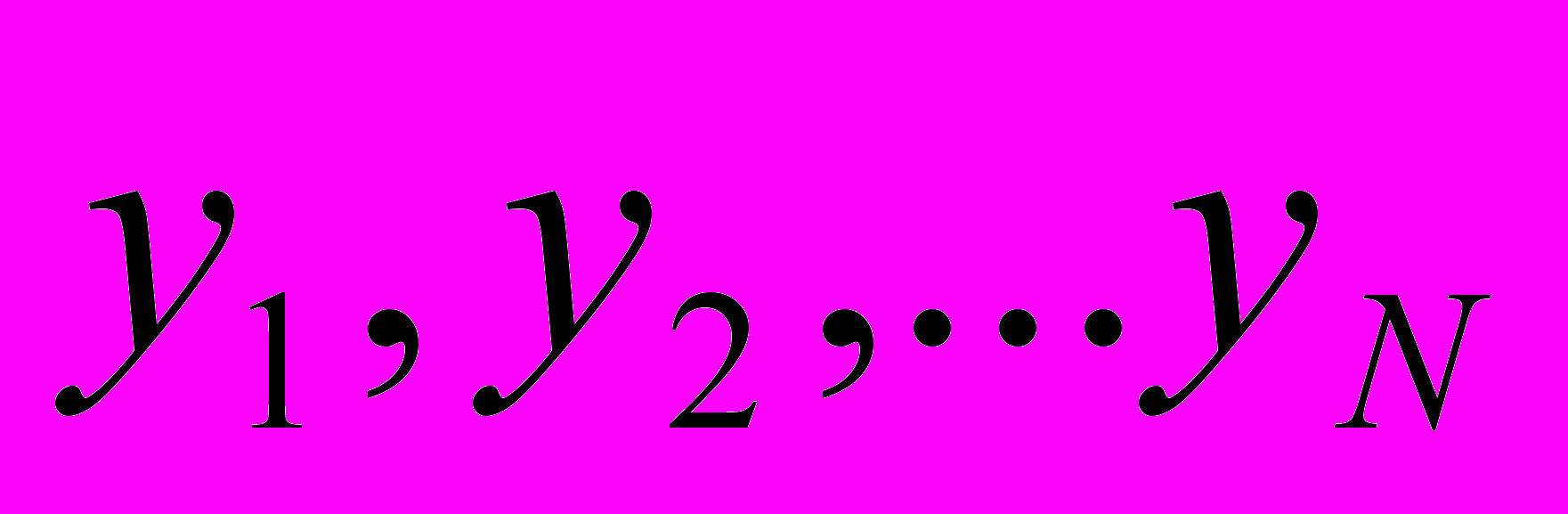.Статистическая обработка этого ряда позволяет определить характеристики M(y) и
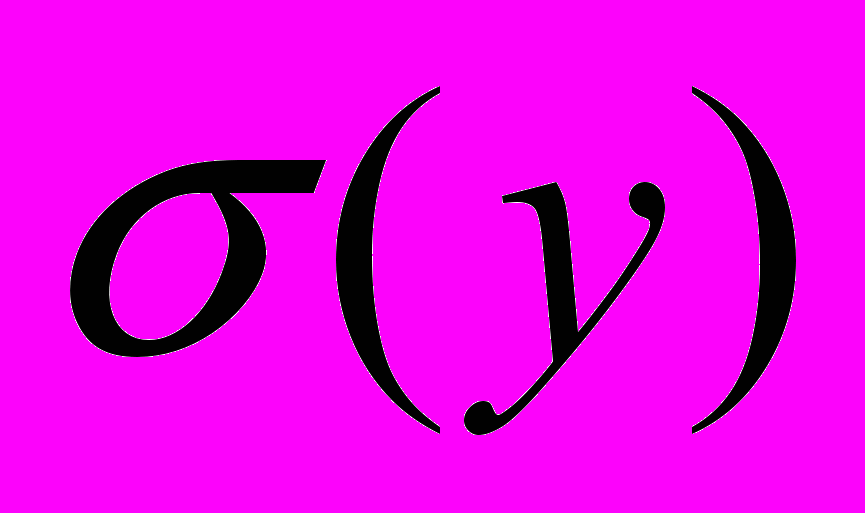.При практической реализации метода Монте-Карло используют математическое или физическое моделирование устройств или процессов. В данном курсовом проекте будем использовать математическое моделирование.
Получив требуемые исходные данные можно приступать к определению точности выходного параметра.
Будем действовать следующим образом:
1. Для начала задаемся числом реализации процесса N=50.
2. Используя генераторы случайных чисел, получаем случайную комбинацию первичных параметров для первой реализации процесса.
3. Подставляем полученную комбинацию значений первичных параметров в математическую модель (1.1) и рассчитываем значение Uвых, соответствующее первой реализации.
4. Действия, описанные в пунктах 2…3, повторяем N раз. В итоге получим ряд
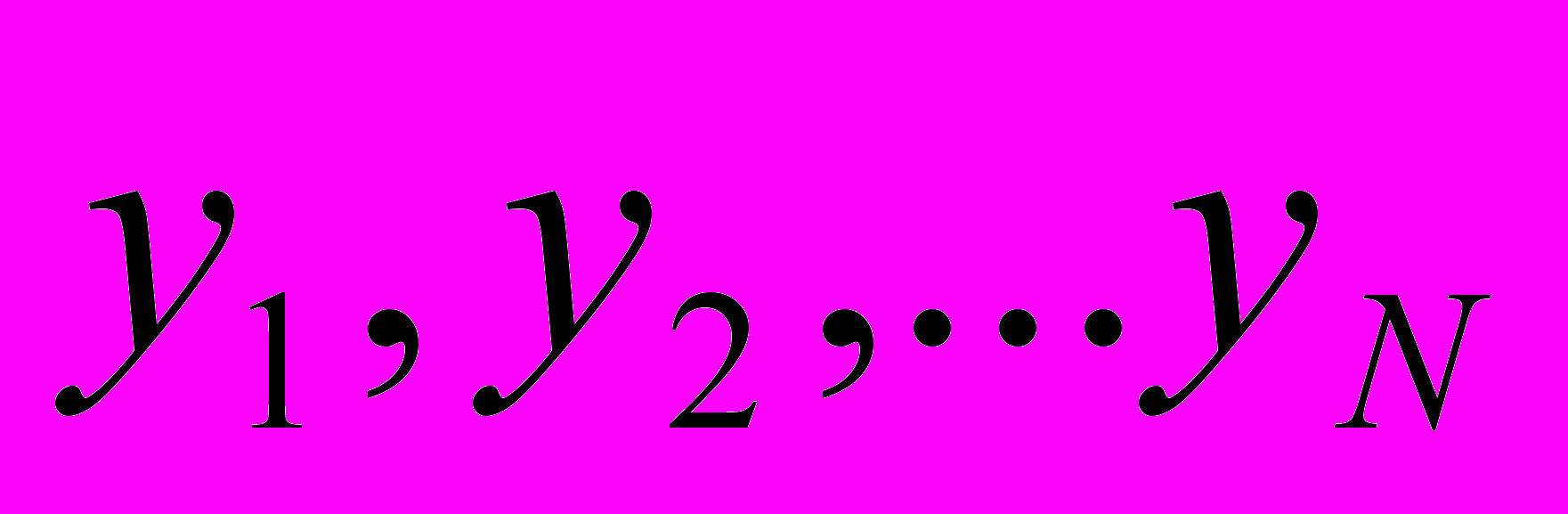.5. Выполняем статистическую обработку полученного ряда и находим характеристики М(у) и
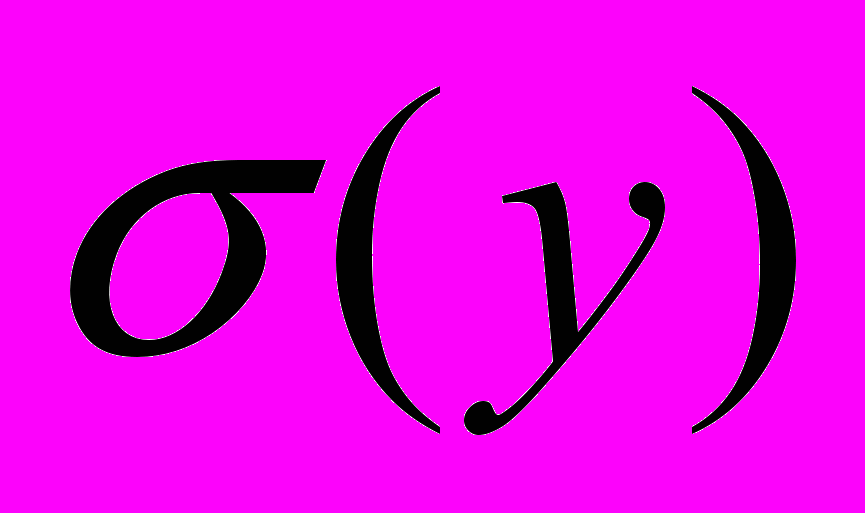.6. Проверяем условие
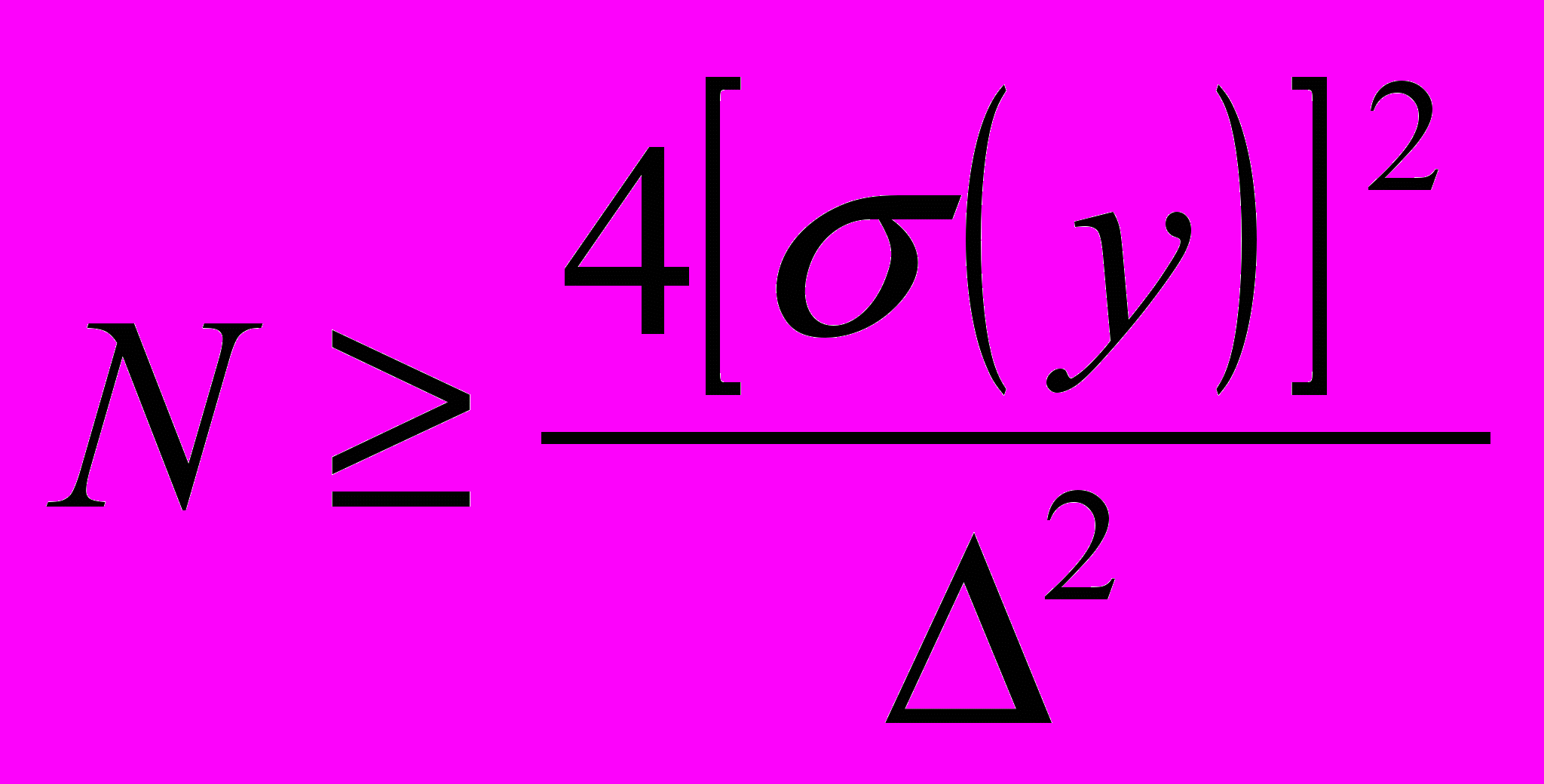, (2.1)где
- заданная до проведения моделирования допустимая погрешность (ошибка) в определении характеристики М(у). =-допустимая ошибка в определении среднего значения параметра , т.е. разница между оценкой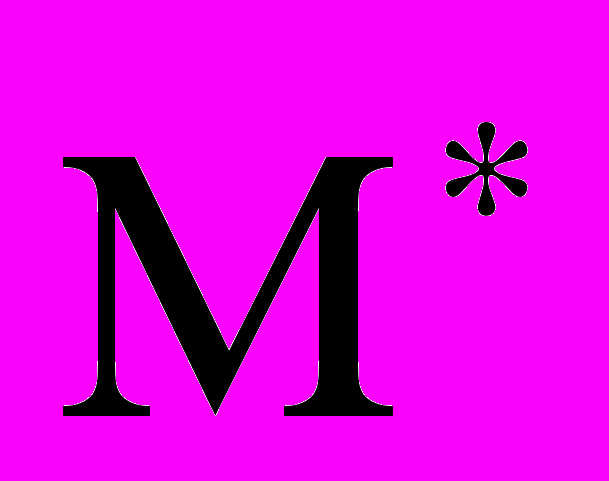 
(y) и истинным значением математического ожидания М(y) , которая еще допускается. Допустимая ошибка назначается из условия=(0.1…0.01)
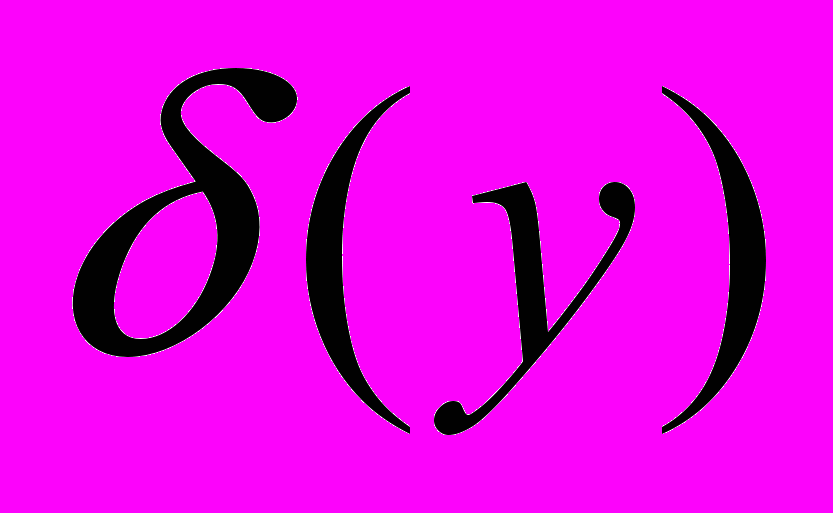. (2.2) Мы задаемся ошибкой =0.01
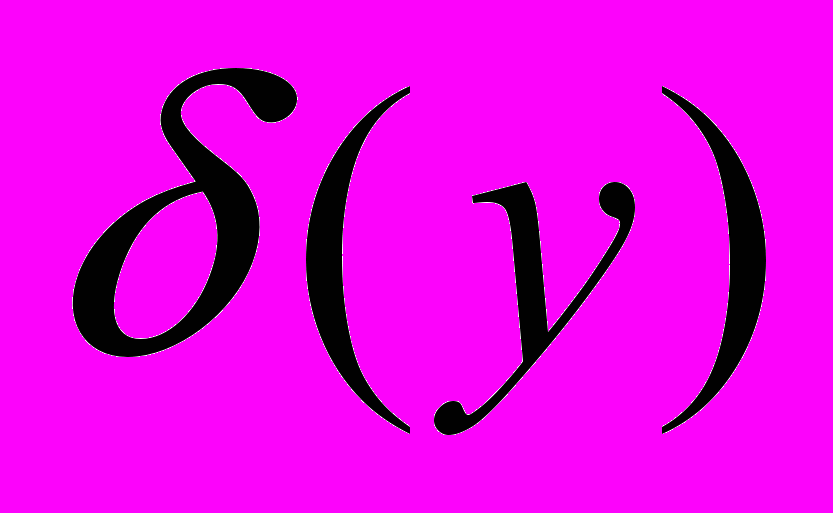
Если условие выполняется, то устанавливаем значение допуска на выходной параметр. Если условие не выполняется, увеличиваем число реализаций процесса, корректируем значение
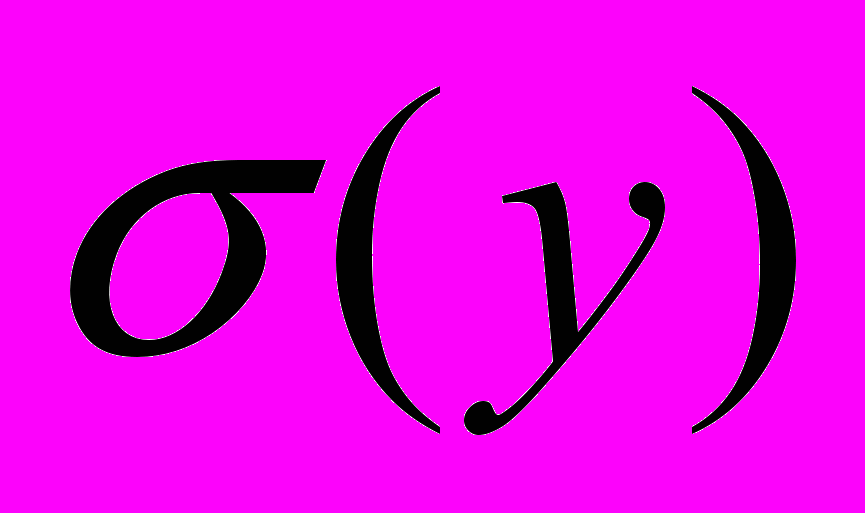и вновь по условию (2.1) проверяем, достигнута ли заданная точность.2.2.Вероятностный метод
Запишем уравнение относительной производственной погрешности выходного параметра
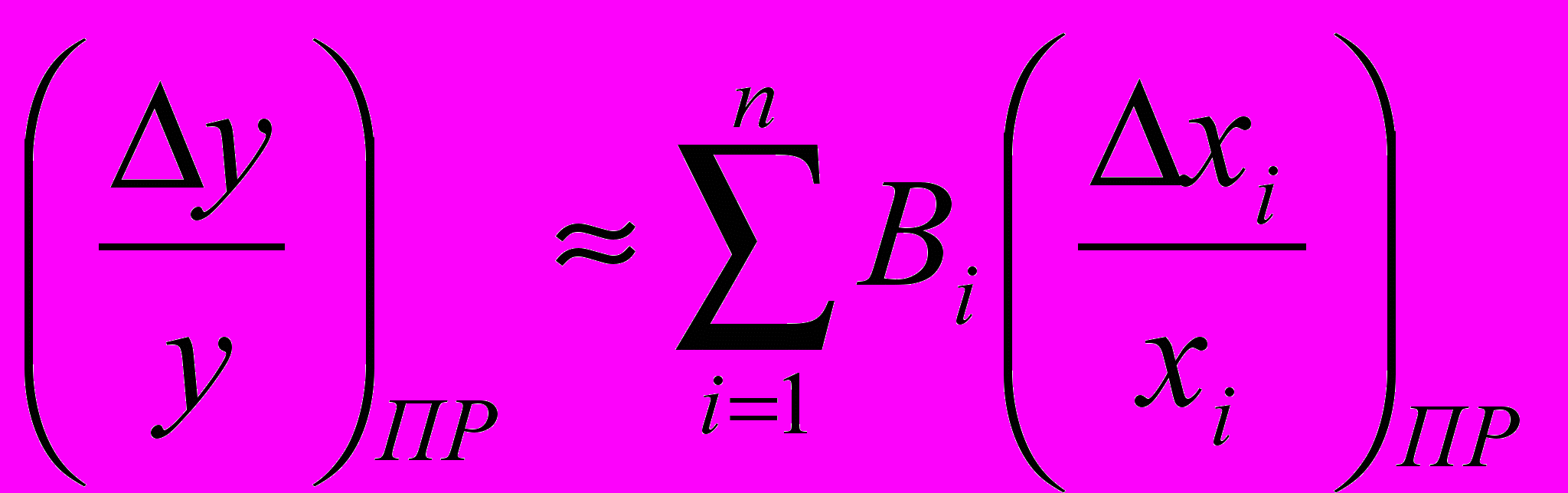. (2.3)Коэффициент влияния i-того первичного параметра
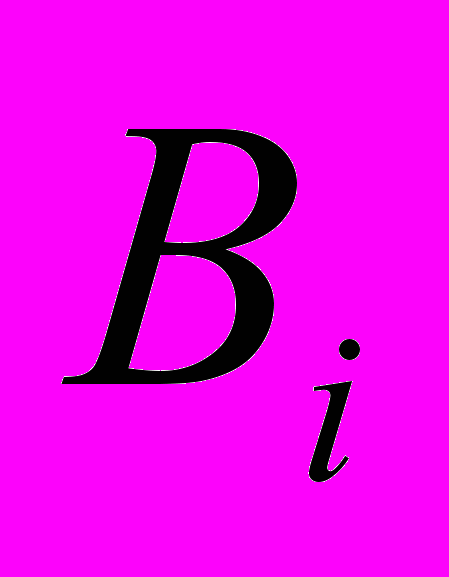определяется как
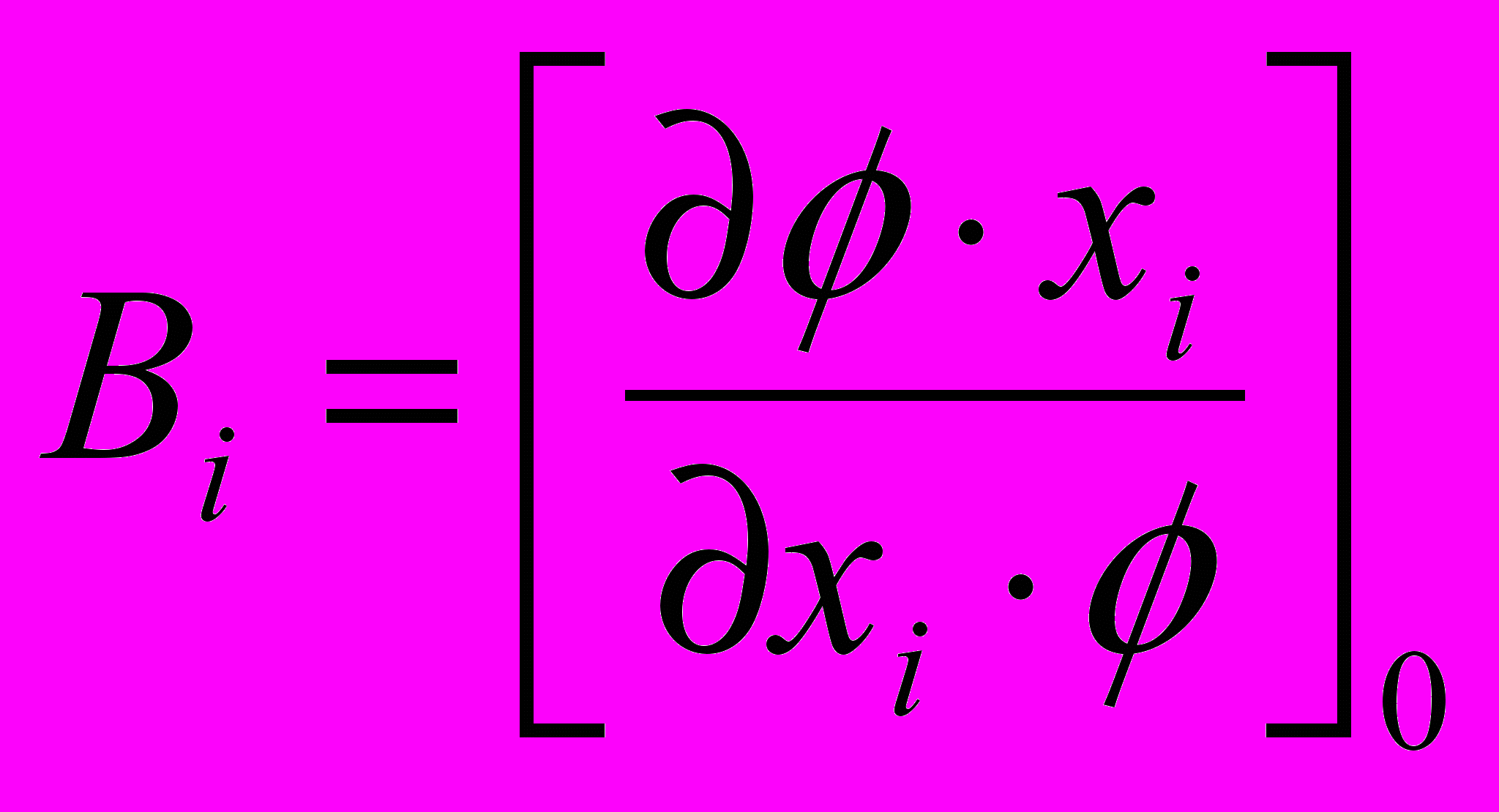. (2.4)При вероятностном методе записанным уравнением воспользоваться сразу не представляется возможным, так как неясно, какие конкретно численно значения
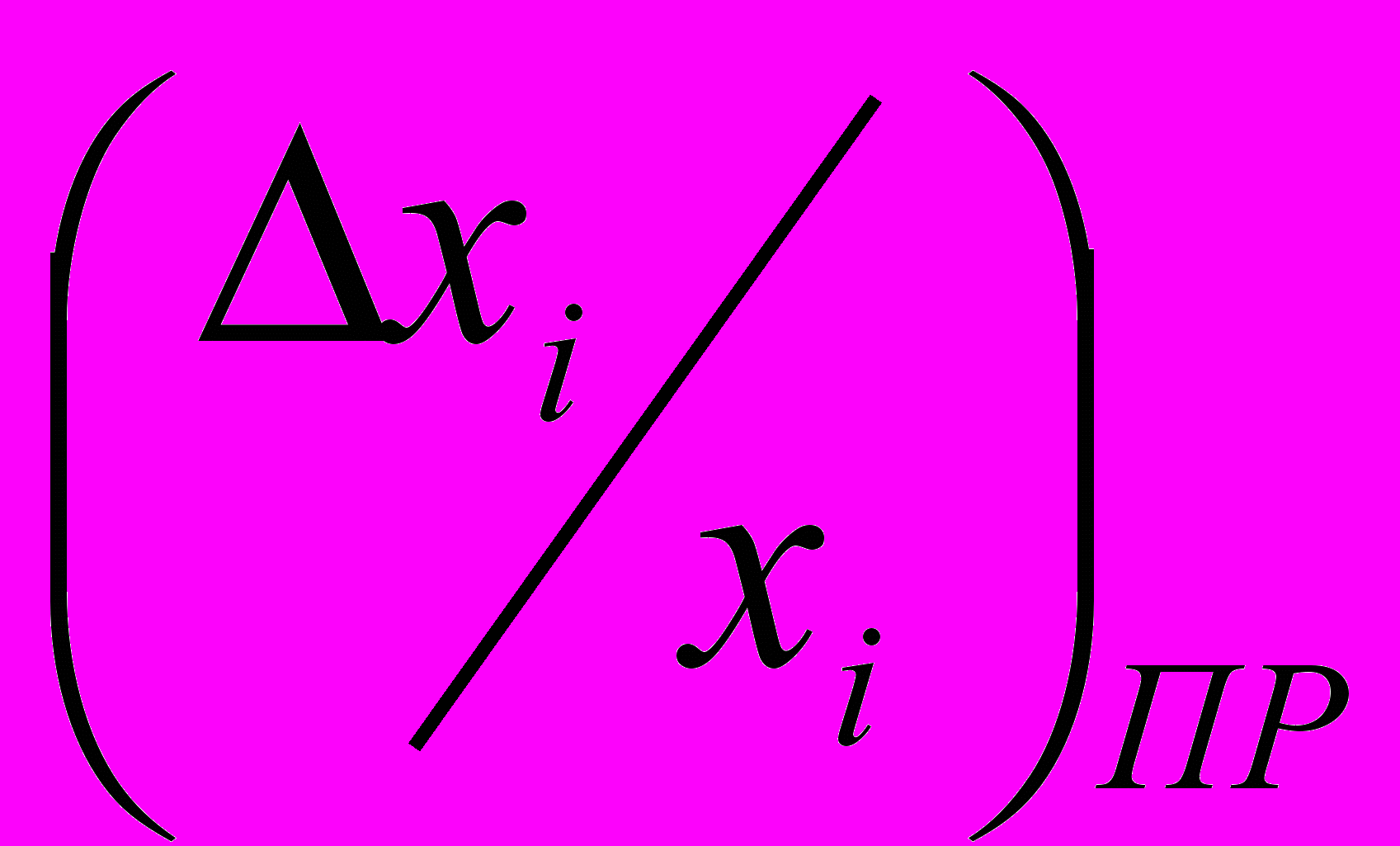требуется подставлять в записанное уравнение в силу случайности этих величин.Поэтому
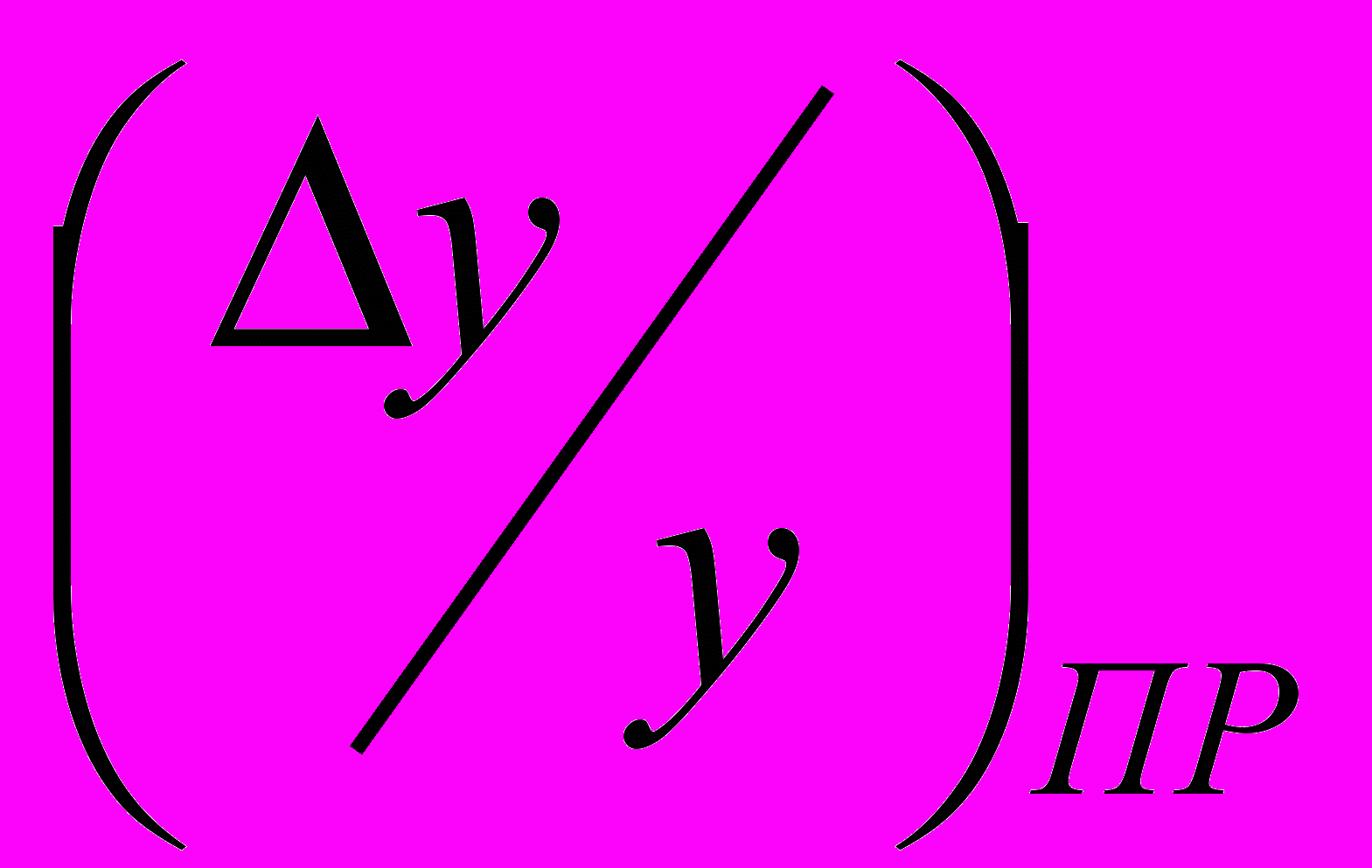также оказывается случайной, и для количественного ее описания используют две характеристики:
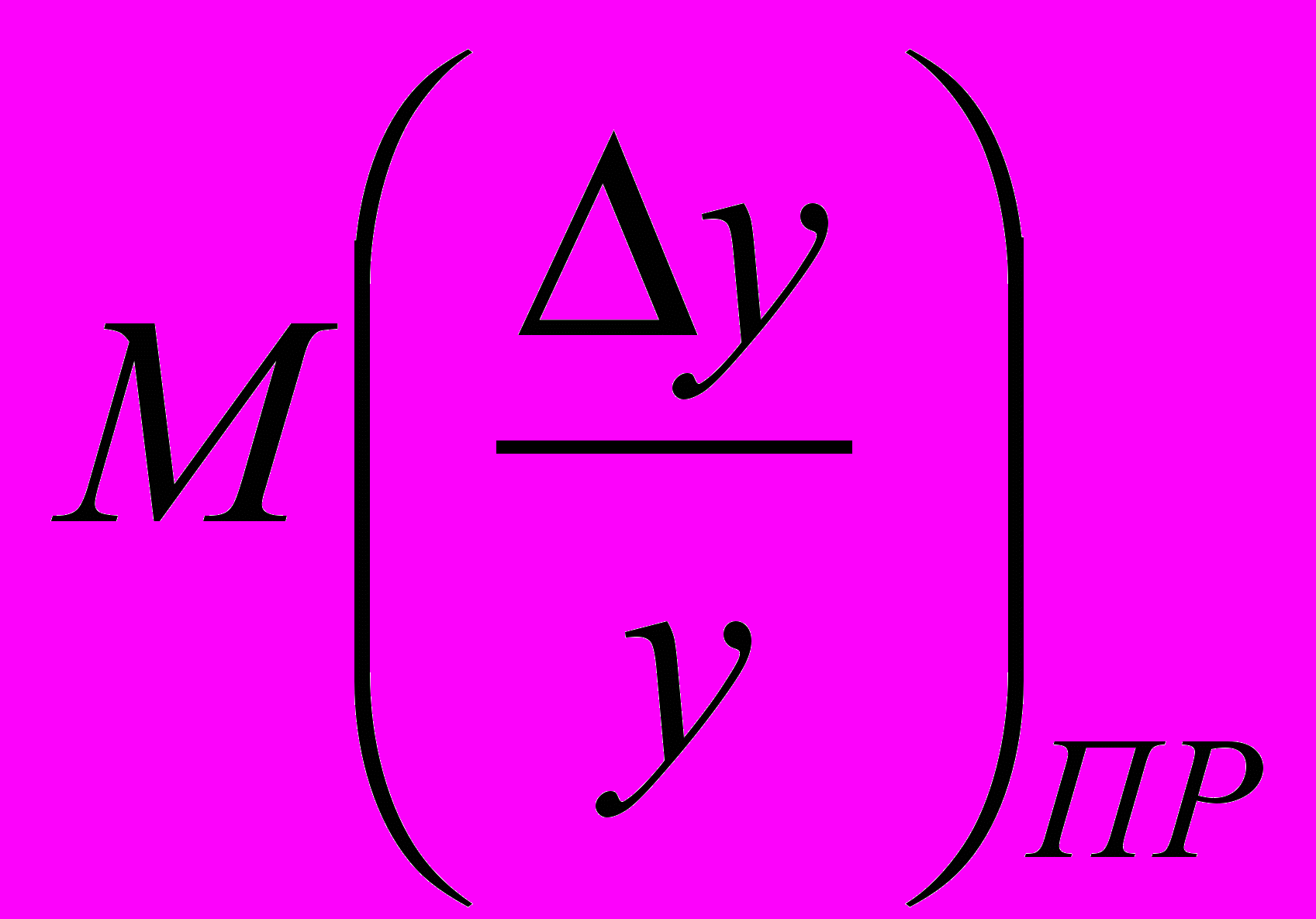-математическое ожидание относительной производственной погрешности выходного параметра;
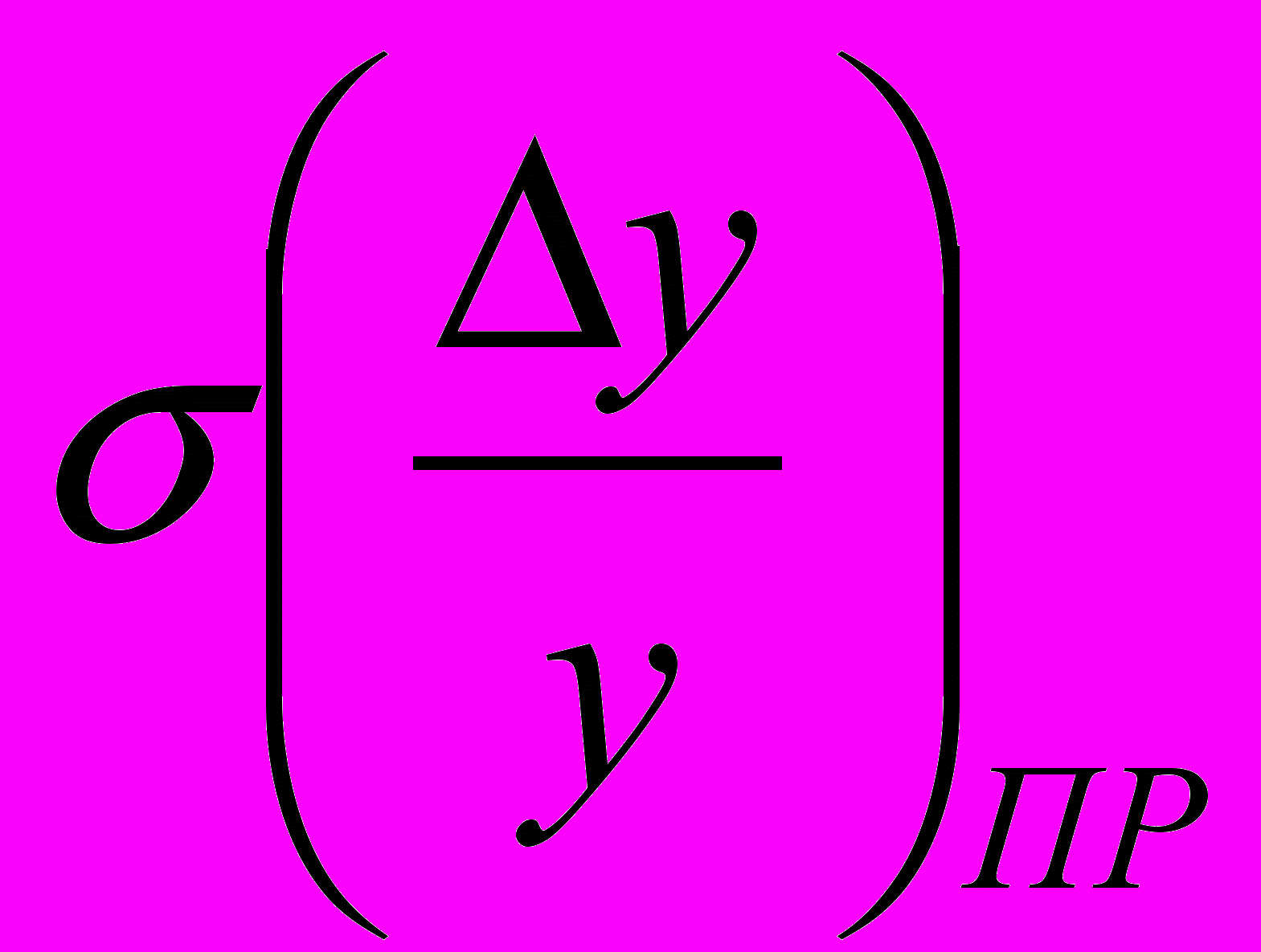-среднее квадратическое отклонение относительной производственной погрешности выходного параметра 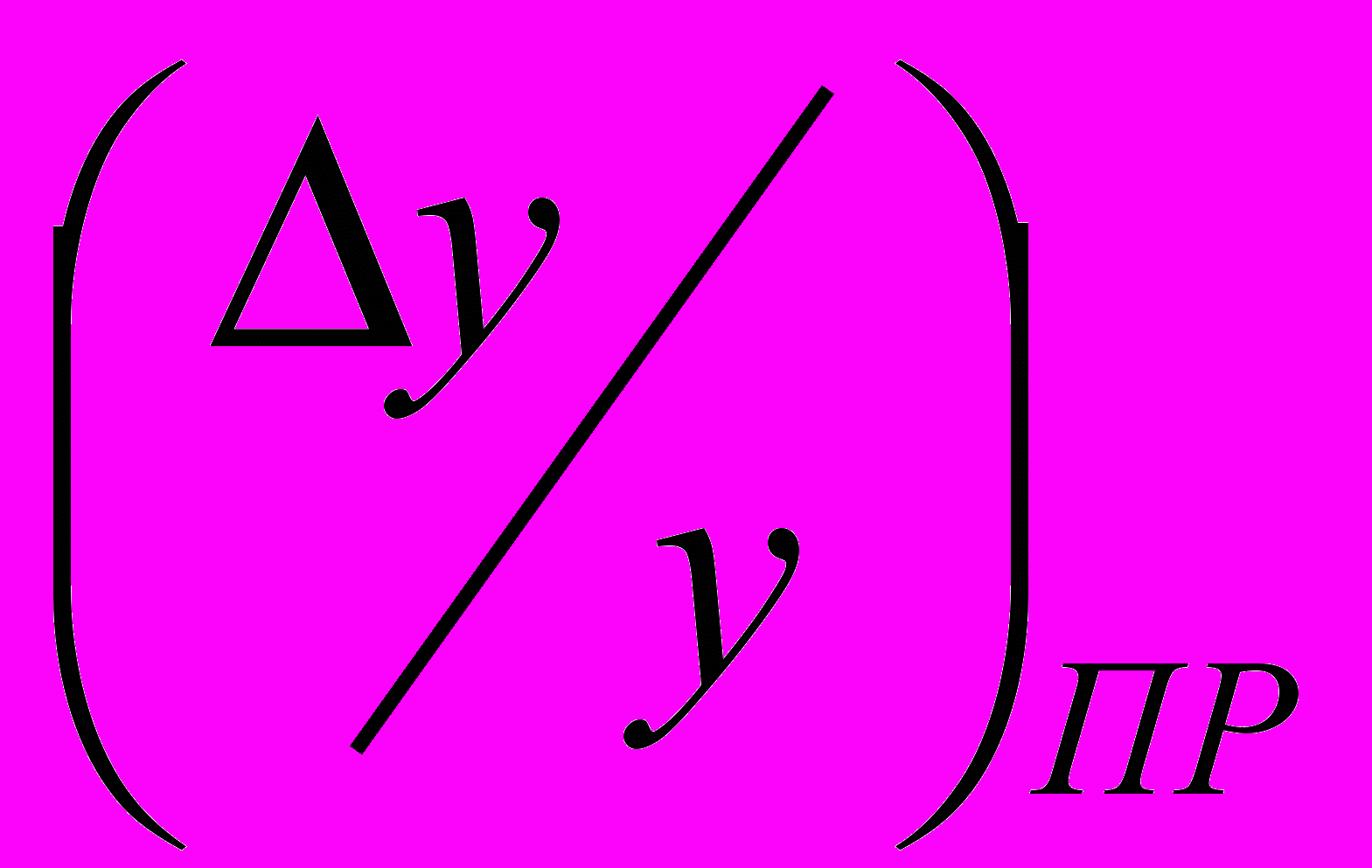.Указанные характеристики могут использоваться для оценки точности выходного параметра. В промышленности в качестве комплексной оценки точности выходных параметров используется производственный допуск на выходной параметр, который устанавливается на основе двух выше записанных характеристик.
Интересующие нас расчетные соотношения записываются в виде
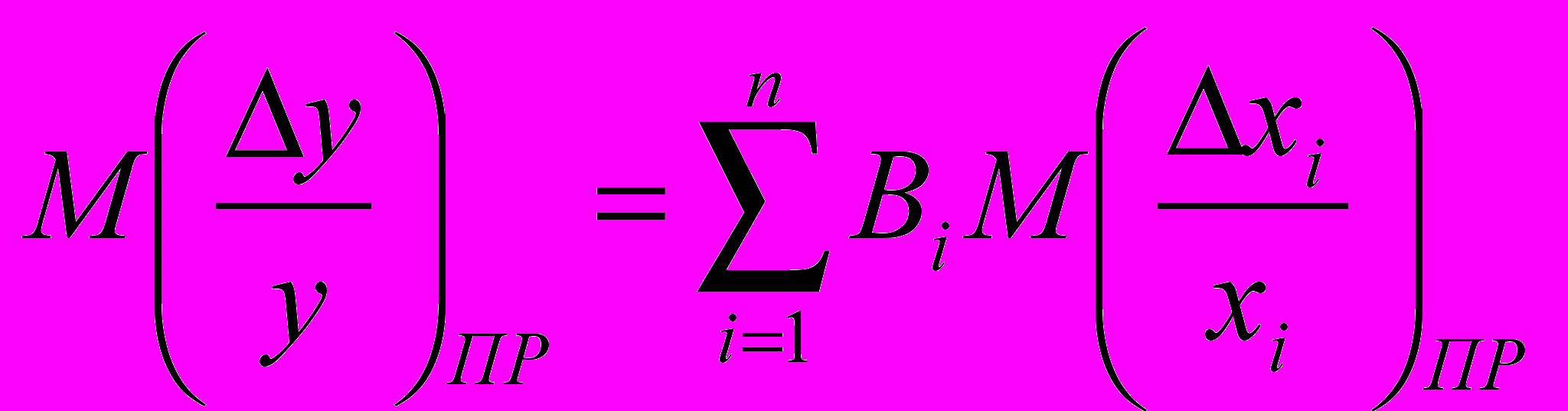, (2.5)где
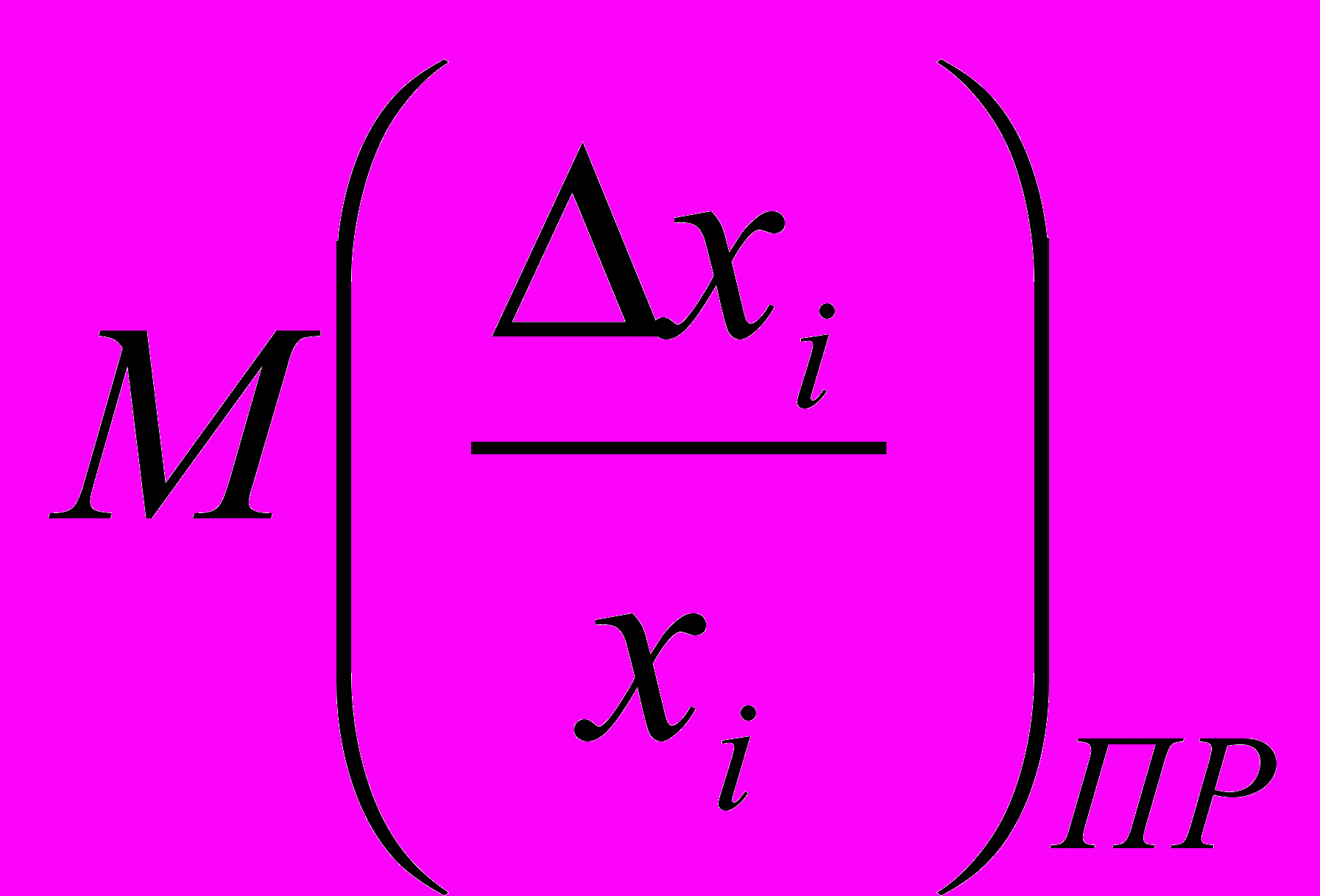-математическое ожидание относительной производственной погрешности i-того первичного параметра;
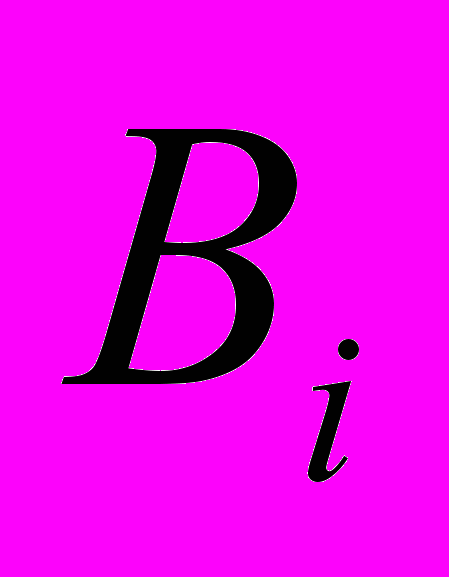-коэффициент влияния i-того первичного параметра.Для
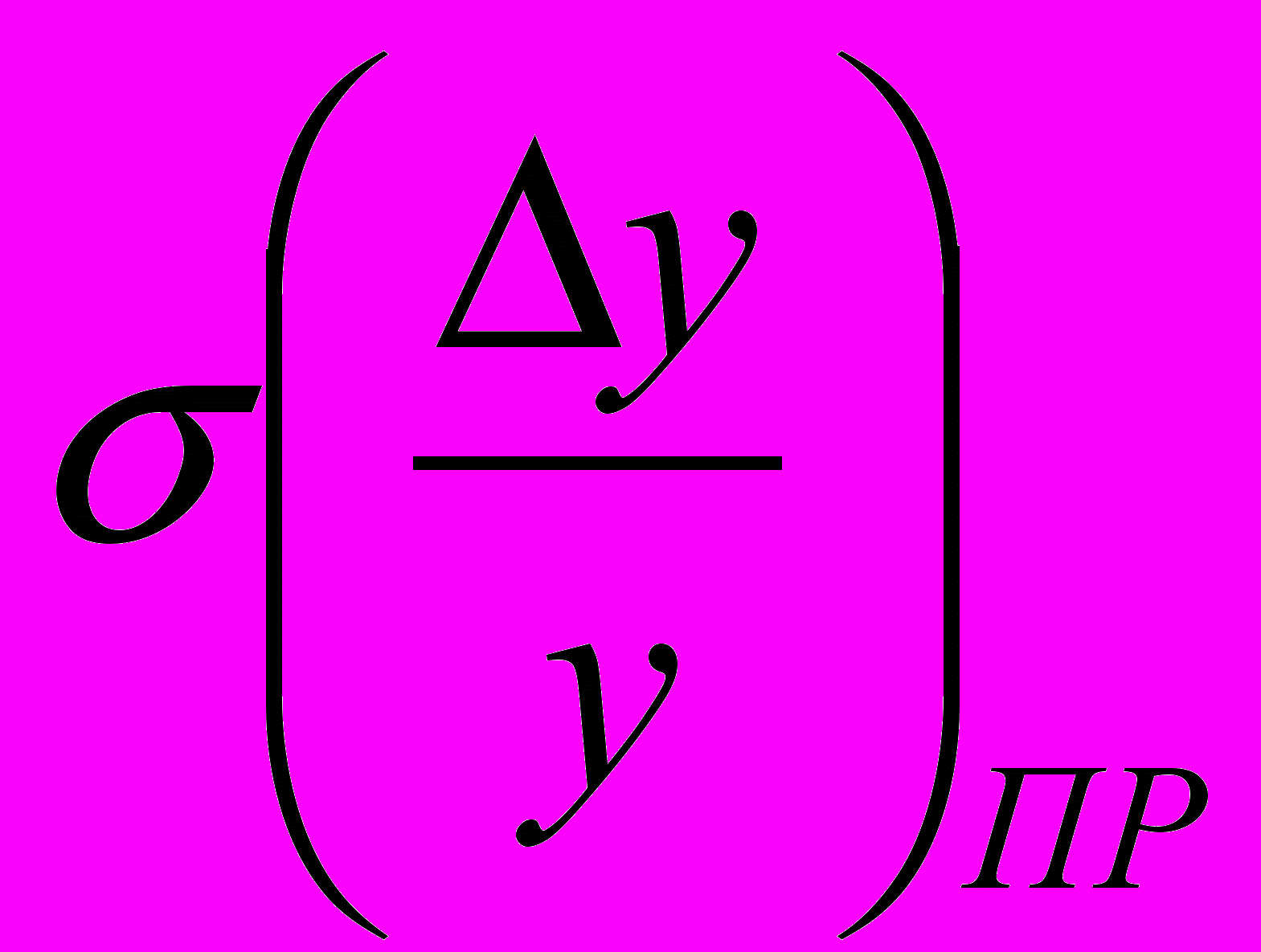воспользуемся выражением :
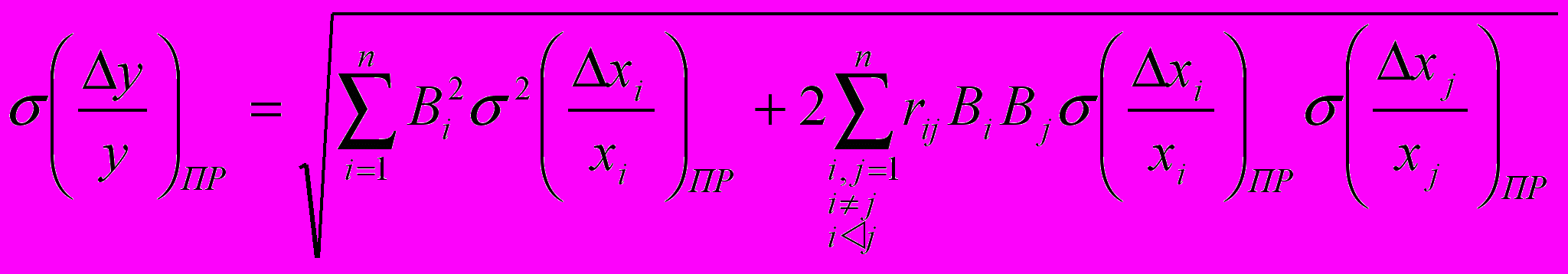, (2.6)где
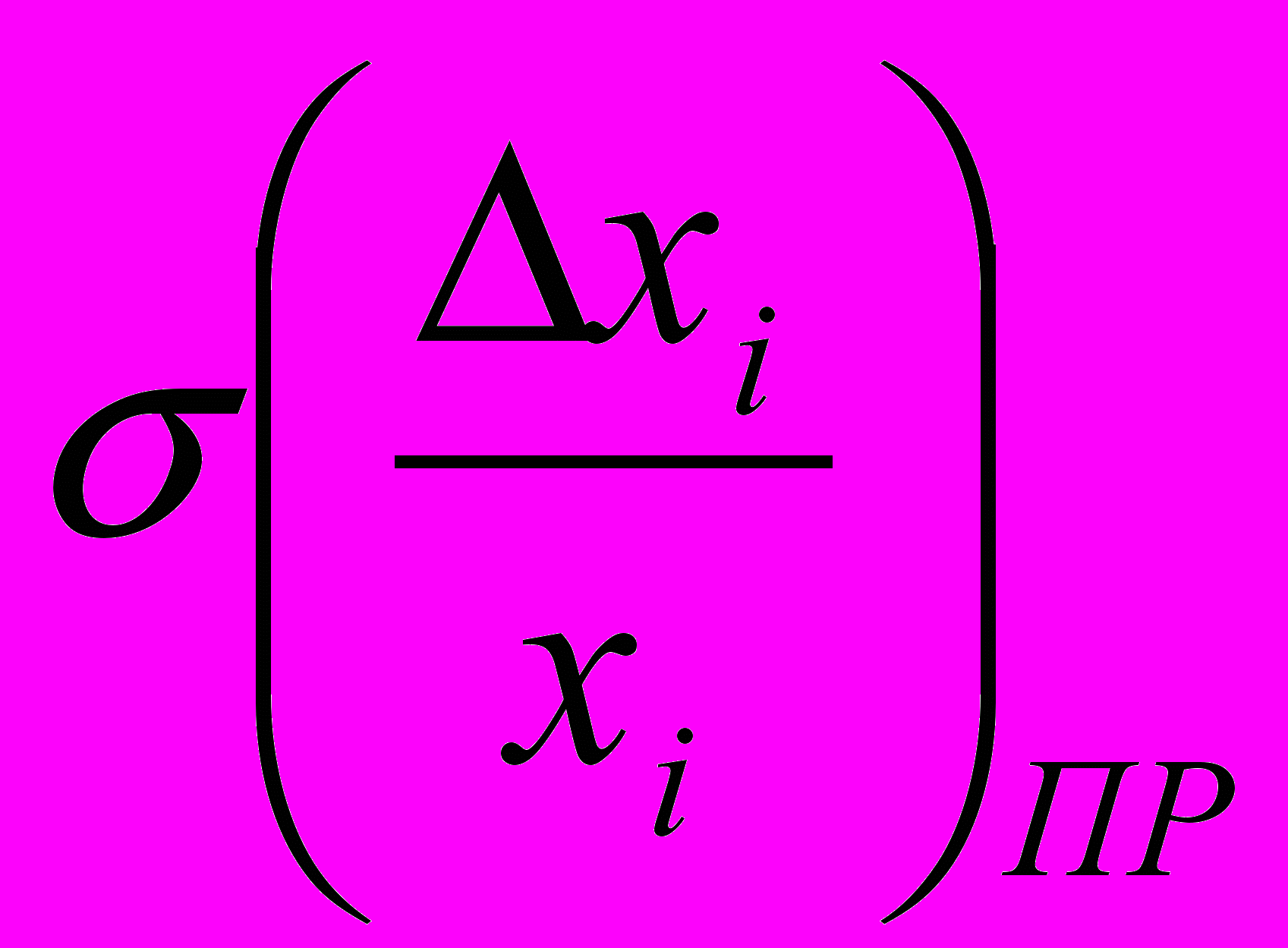-СКО первичного параметра;
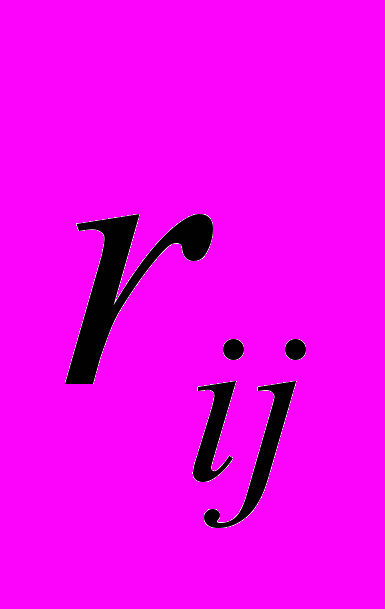-коэффициент корреляции между i-м и j-м первичными параметрами.3.Решение задачи вероятностным методом
Для решения задачи нам нужно определить коэффициент влияния каждого первичного параметра по формуле (2.4) .
; 
;
;
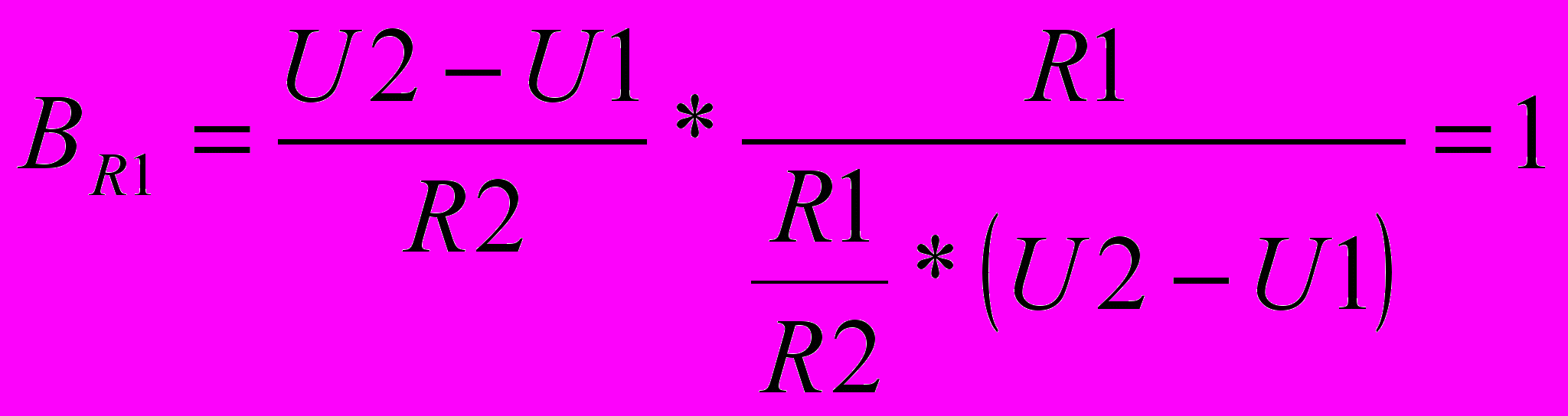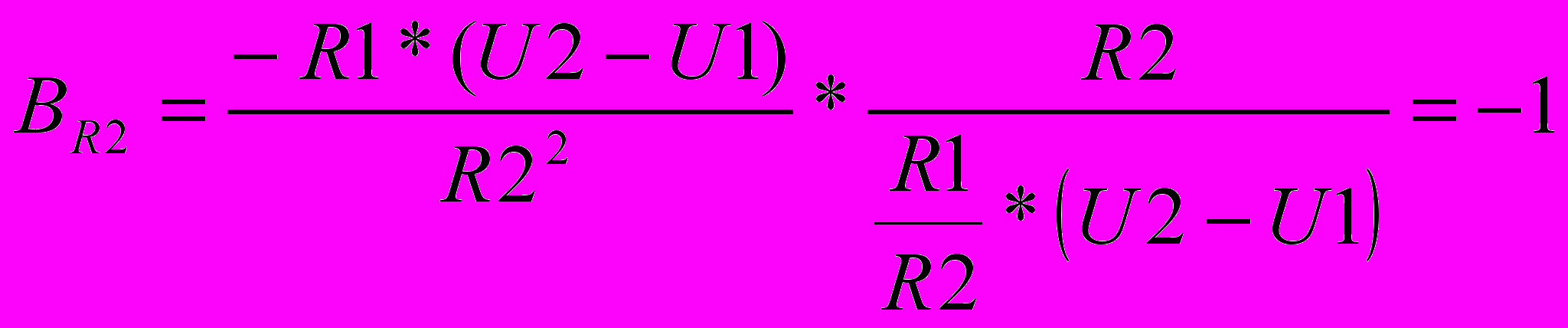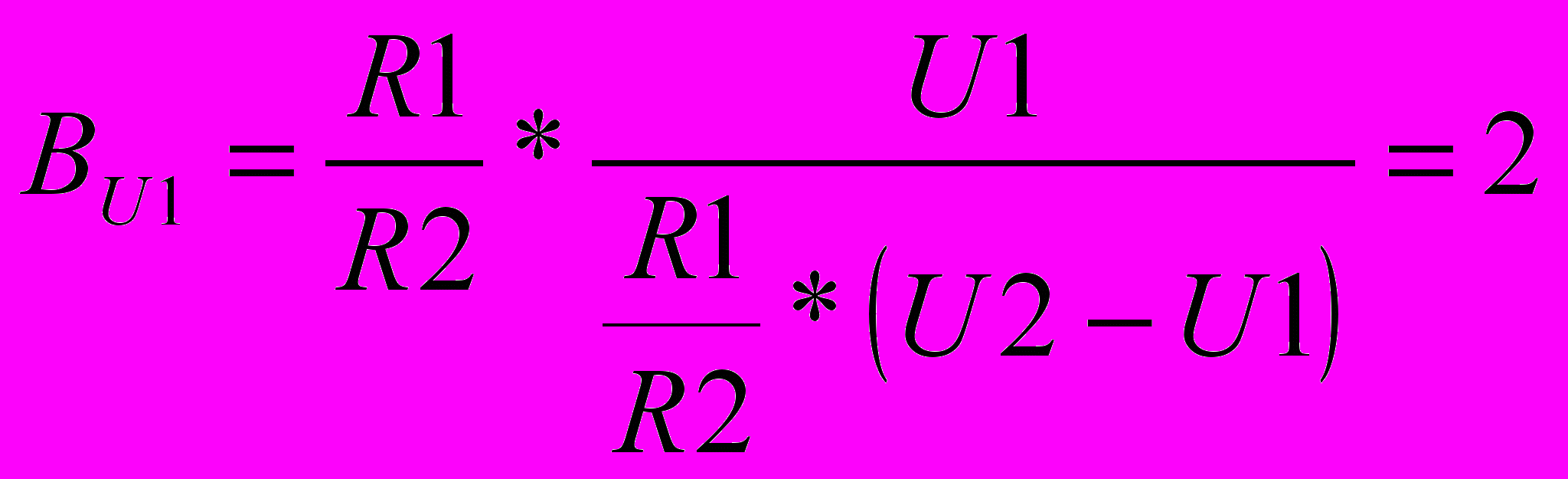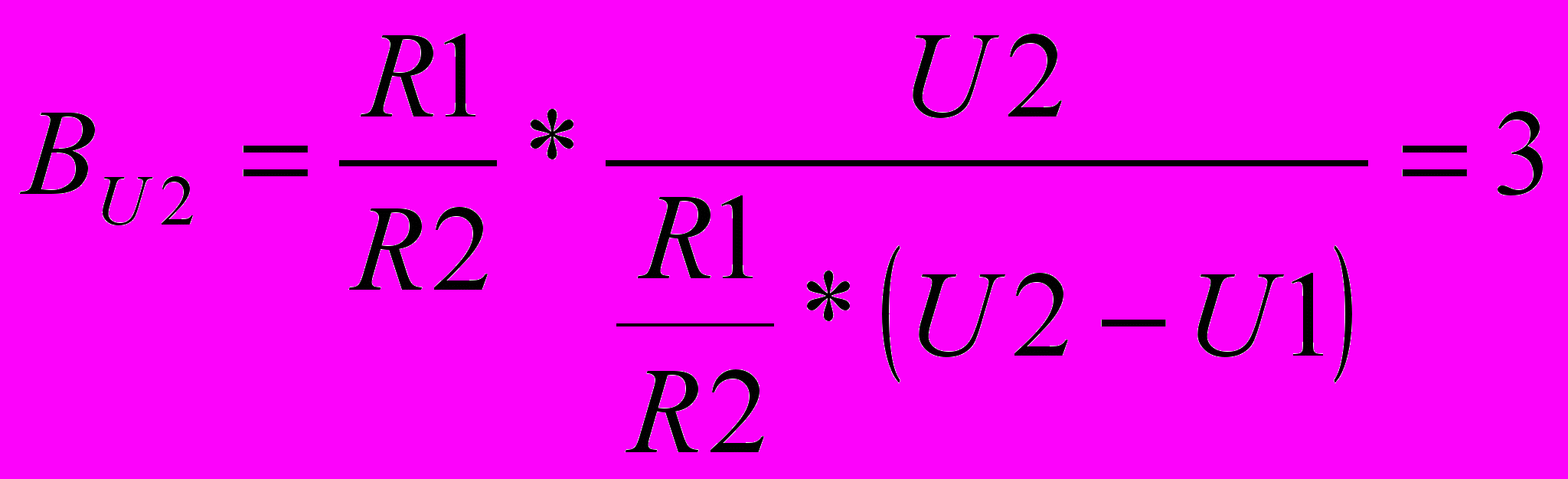.Что бы воспользоваться формулой (2.6) нам также необходимо рассчитать значение
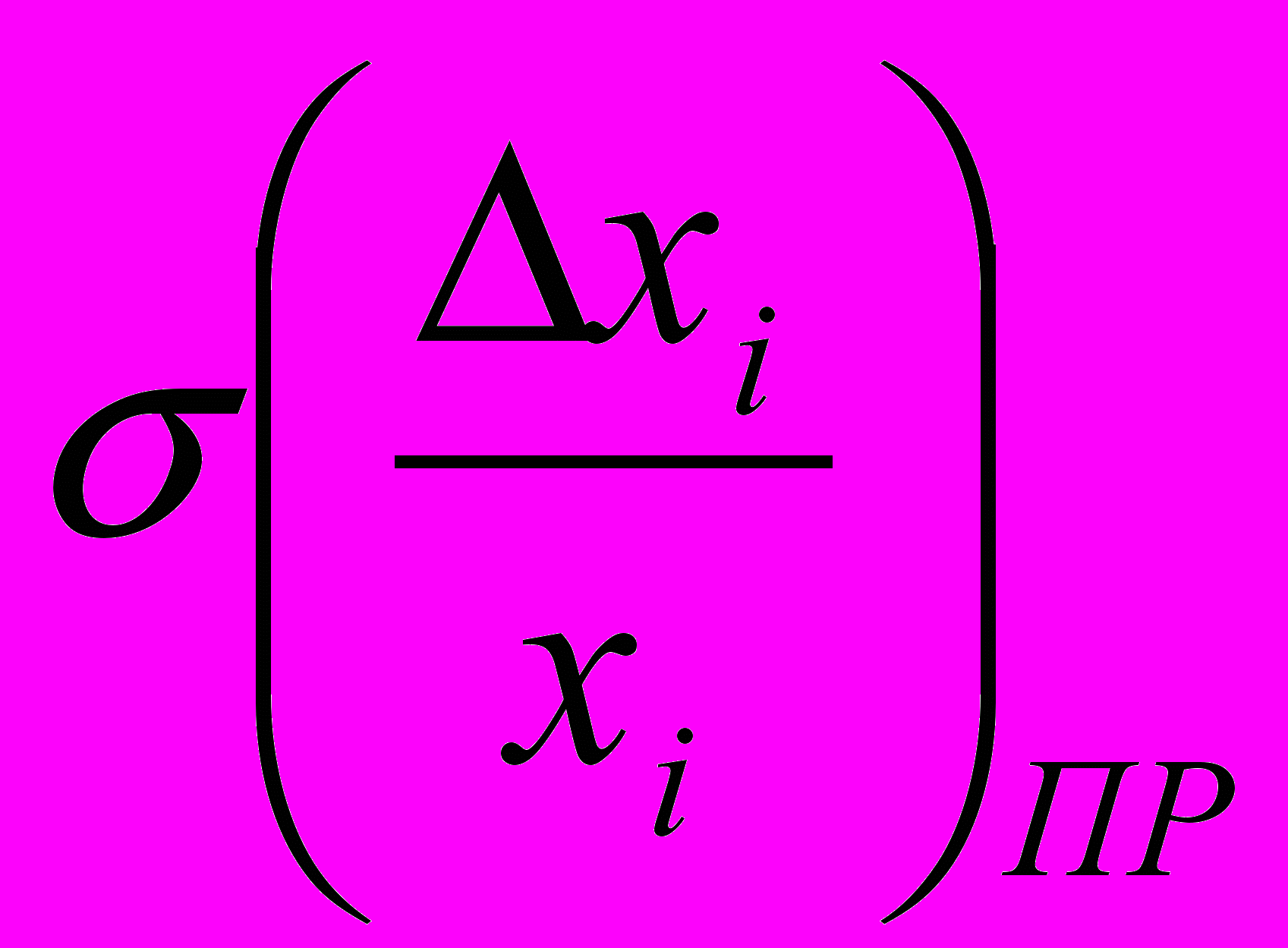,его находим по “правилу трех сигм “, так как все наши первичные параметры распределены по нормальному закону.
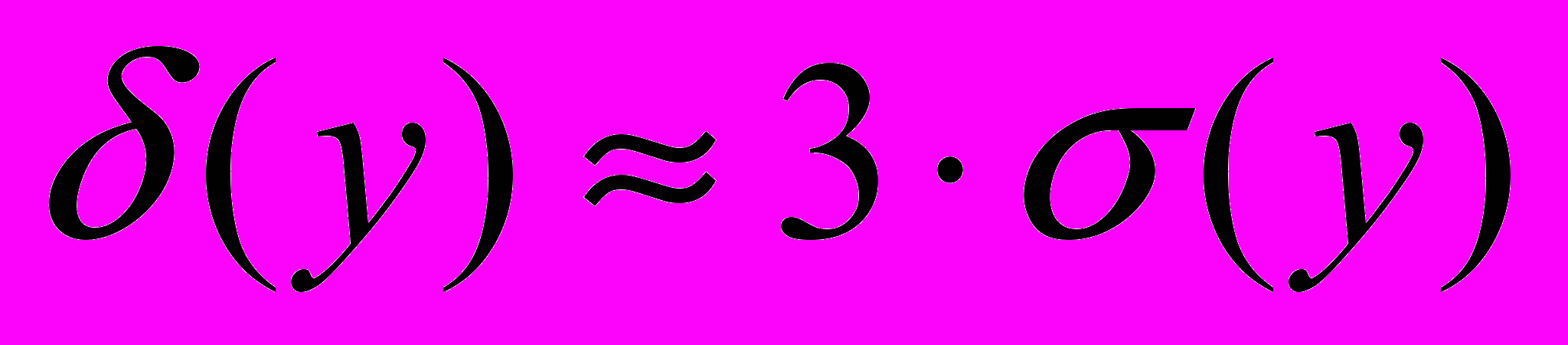. (3.1)Затем определяем СКО выходного параметра по формуле (2.6).
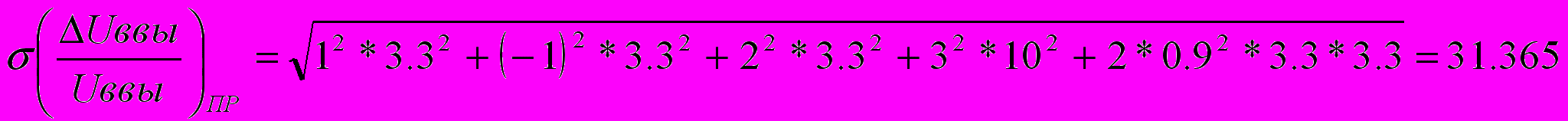%,4.Рализация метода Монте-Карло на ЭВМ
Для решения поставленной задачи мы пользовались языком программирования Паскаль 7.0.
Структурная схема реализации алгоритма решения задачи анализа точности выходных параметров методом Монте – Карло на ЭВМ представлена в приложении. Требуется получить численные значения математического ожидания и среднее квадратическое отклонение выходного параметра.
Вначале мы вводим значения первичных параметров М(xi) и (xi), после организуем цикл n=50 реализаций. Для каждой из реализаций выходного параметра генерируются значения первичных параметров
с учетом нормального закона распределения по выражению
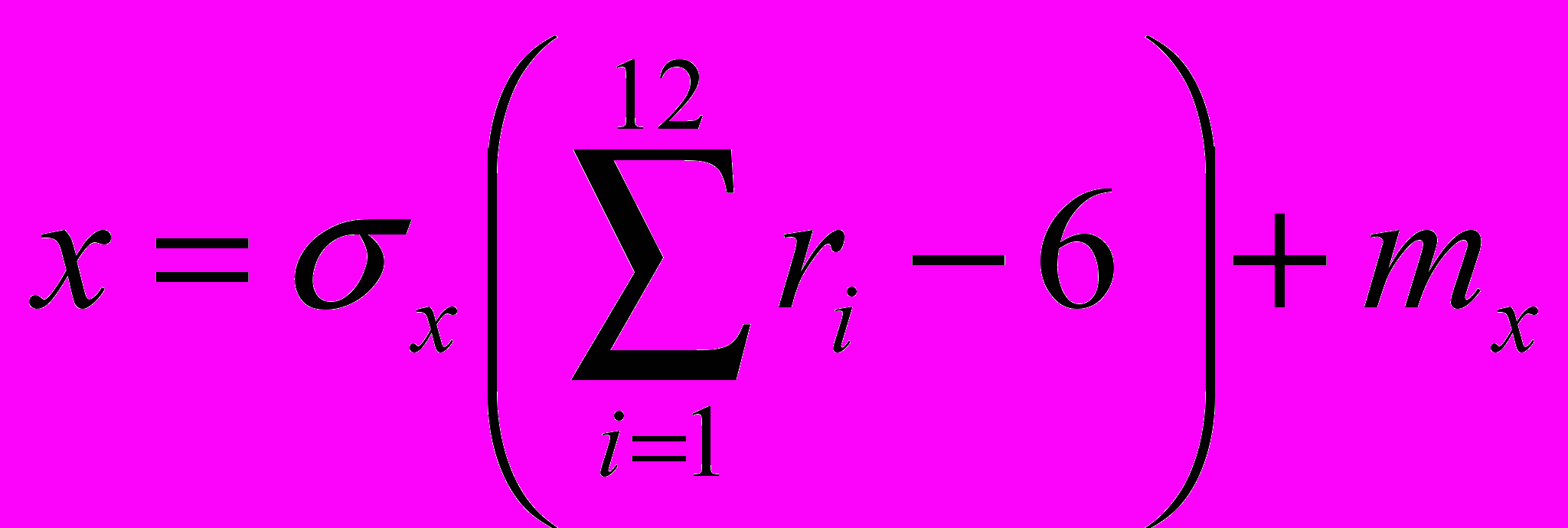, (4.1)где x - нормально распределенная случайная величина;
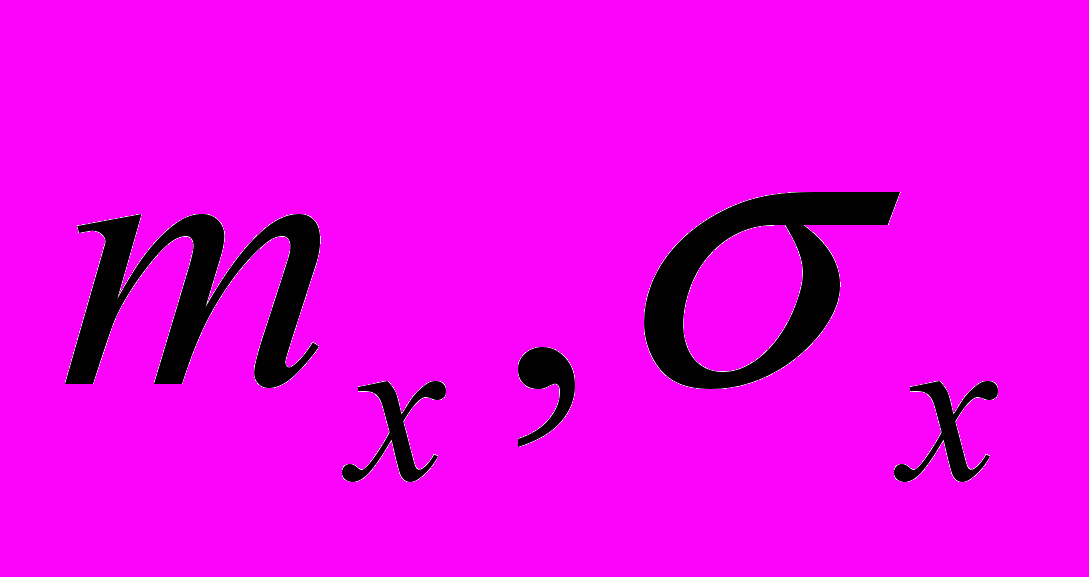- математическое ожидание и СКО x;
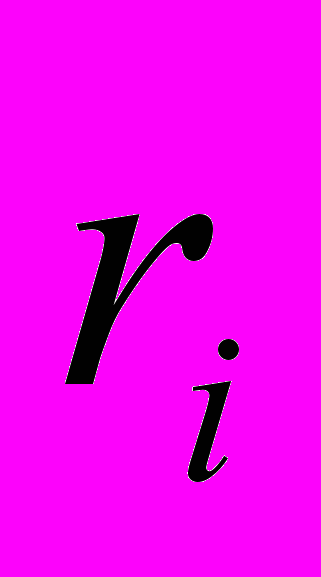- равномерно распределенное число в диапазоне (0…1).Далее генерируются значения первичных параметров с учетом нормального закона распределения с коэффициентом корреляции равного 0.9.
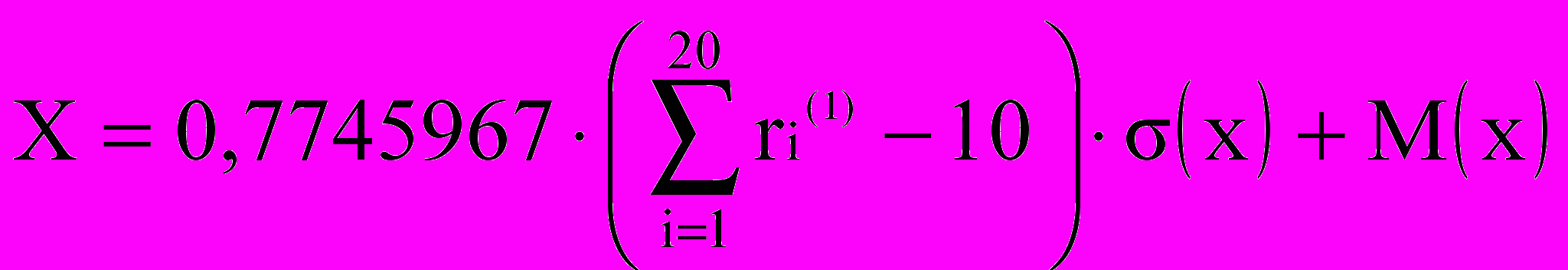, (4.2)
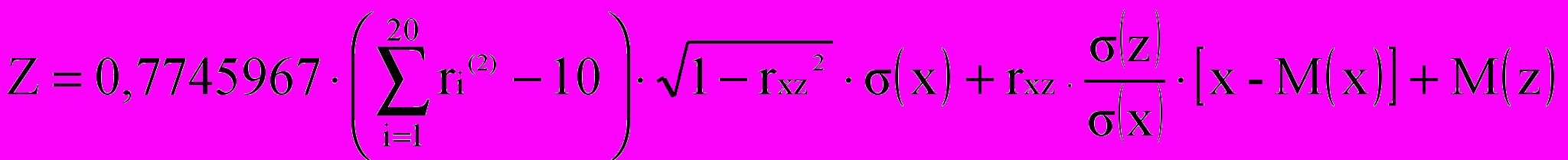, (4.3)где Х – значение не коррелированного значения;
Z – значение параметра, коррелированного с параметром Х;
М(х),(х)–математическое ожидание и среднее квадратическое отклонение параметра Х;
М(z),(z)–математическое ожидание и среднее квадратическое
отклонение параметра Z;
rxz – коэффициент корреляции между параметрами Х и Z;
ri(1),ri(2)–последовательности случайных равномерно
распределенных чисел в диапазоне (0…1), полученные
соответственно в первом и втором циклах.
Получив значения первичных параметров, подсчитываем выходное напряжение по формуле (1.1). Затем идет подсчет математического ожидания и СКО выходного параметра .
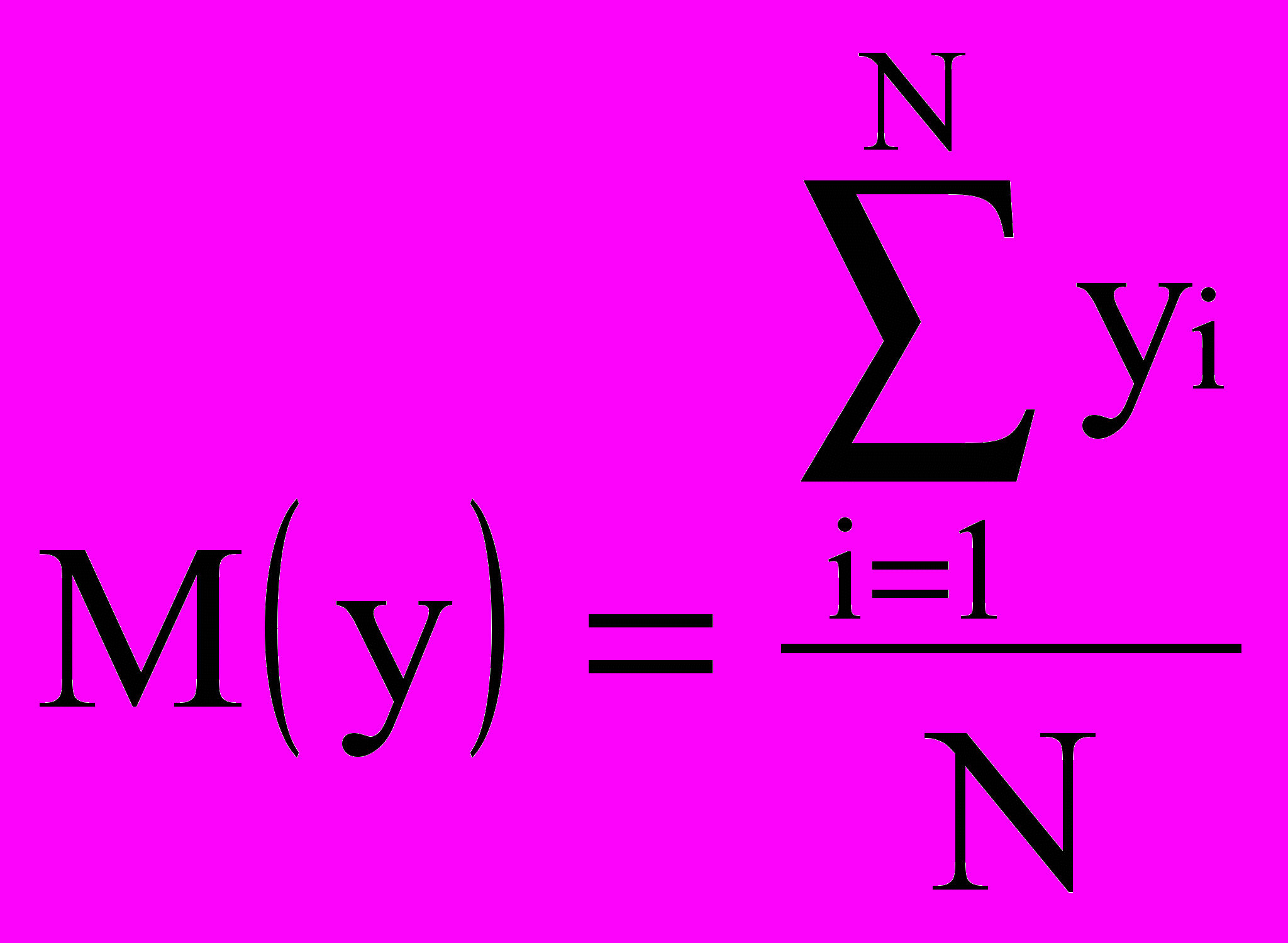, (4.4)
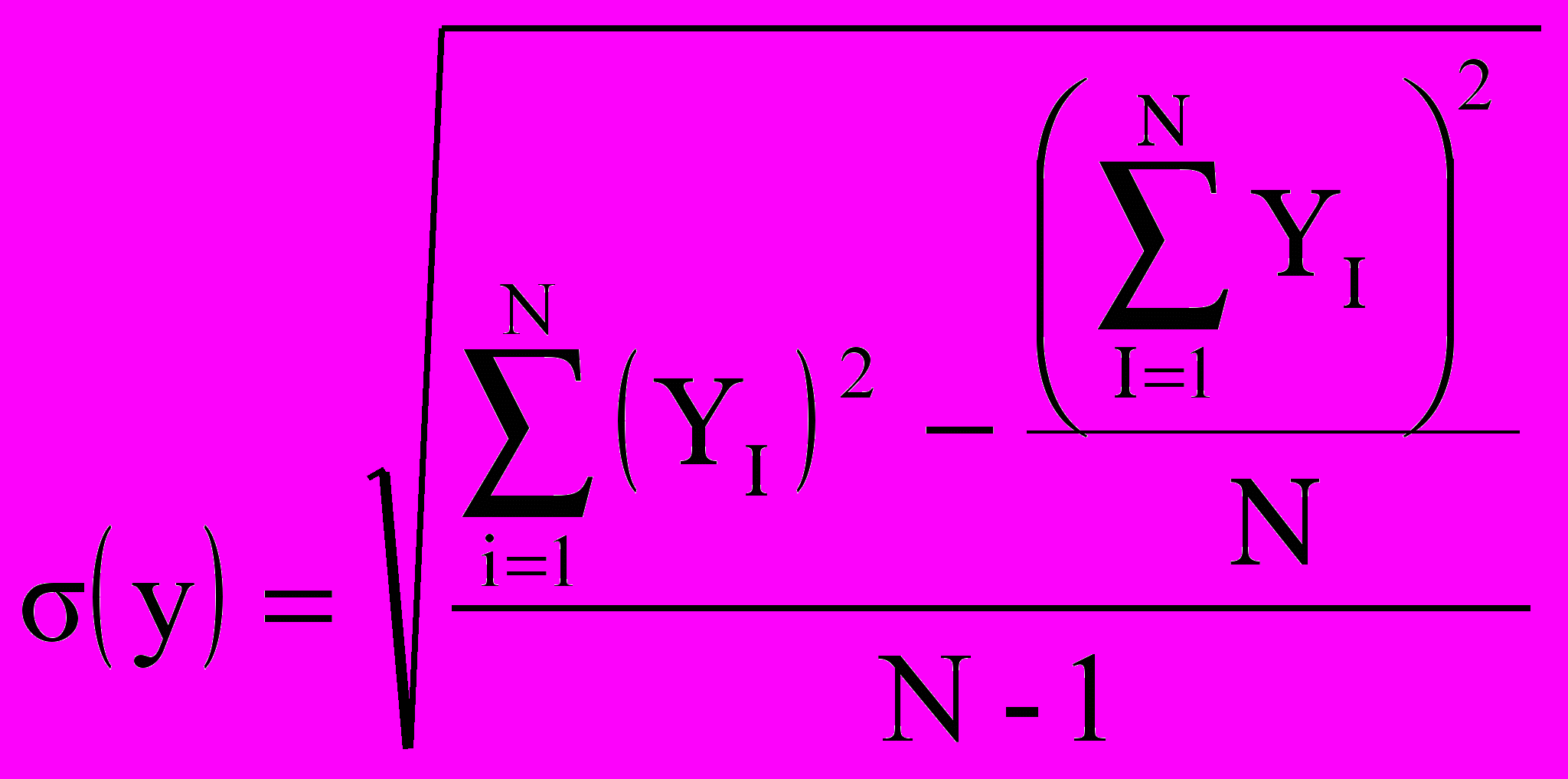, (4.5)где М(y),(y) – математическое ожидание и среднее квадратическое отклонение выходного параметра y;
yi – значение выходного параметра в i-ой реализации;
N – количество реализаций.
Далее проверяется условие (2.1). Если условие выполняется, то полученное математическое ожидание М(y) определено с ошибкой, не превышающей заданное значение , и гарантируется с вероятностью (=0.95). Если же условие не выполняется, то поступают следующим образом. Добавляют еще некоторое значение реализаций и повторяют выше описанное до тех пор, пока условие (2.1) не выполнится.
Необходимое пояснение приведено в таблице 3.1.
Таблица 4.1
Пояснение функциональных частей структурной схемы алгоритма решения задачи на ЭВМ методом Монте – Карло.
| Номер функциональной части | Назначение |
| 1,19 | Функциональные блоки схемы |
| 8,16 | Выбор направления выполнения алгоритма в зависимости от переменных условий |
| 2 | Ввод начальных данных (математическое ожидание R1,R2,U1,U2;средне квадратичное отклоненияR1,R2,U1,U2) |
| 3,6,11,14 | Организация цикла по индексу i |
| 4,12 | Получение первичных параметров с нормальным распределением по формуле (4.1) |
| 5,13 | Получение первичных коррелированных параметров с нормальным распределением по формуле (4.2),(4.3) |
| 7,15 | Вычисление выходного напряжения по выражению (1.1) |
| 9,17 | Статистическая обработка результатов (нахождение М(х),(х) по формуле (4.4),(4.5)) |
| 10 | Уточнение требуемого числа опытов по формуле (2.1) |
Таблица4.2
Список идентификаторов вычислительного алгоритма программы для ЭВМ.
Обозначение параметра | Смысл параметра | |
| В вычислит. алгоритме | В программе | |
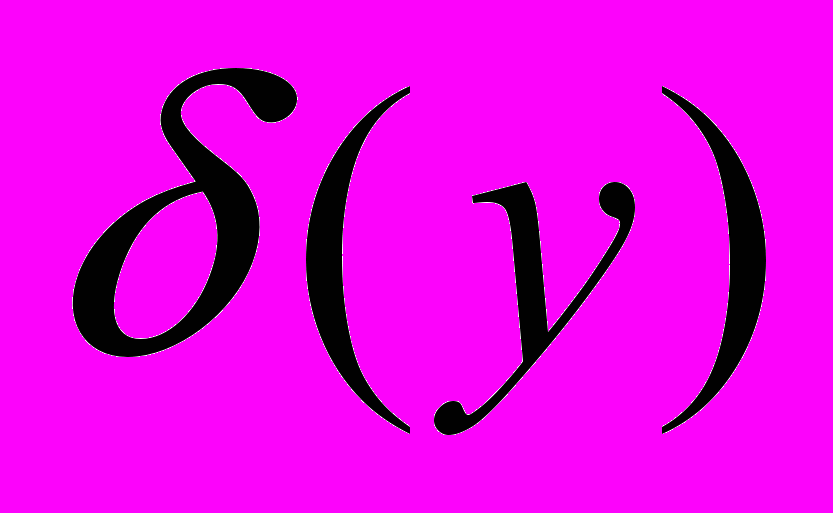| | Deltha | Половина поля допуска |
| | Epsylon | Допустимая погрешность в определении характеристики М(y) |
| М(х) | MR1 | Математическое ожидание сопротивления первого резистора (номинальное значение) |
| MR2 | Математическое ожидание сопротивления второго резистора (номинальное значение) | |
| MU1 | Математическое ожидание сопротивления первого входного напряжения (номинальное значение) | |
| MU2 | Математическое ожидание сопротивления второго входного напряжения (номинальное значение) | |
| | N | Определяемое число реализации процесса |
| N | N_opr | Определённое число реализации процесса |
| | N_def | Шаг определения количества реализаций процесса |
| | Q | Количество строк в таблице результатов видимой на экране |
| | Q_tab | Количество строк в таблице результатов в текстовом файле |
| | R1 | Сопротивление первого резистора |
| | R2 | Сопротивление второго резистора |
| | U1 | Первое входное напряжение |
| | U2 | Второе входное напряжение |
| (R1) | SR1 | СКО первого резистора |
| (R2) | SR2 | СКО второго резистора |
| (U1) | SU1 | СКО первого входного напряжения |
| (U2) | SU2 | СКО второго входного напряжения |
| (Uвых) | Sygma | Средне квадратичное отклонение выходного параметра |
Вспомогательные и промежуточные параметры | ||
| | с | Буфер ввода |
| | i,j | Счётчик |
| | s | Аккумулятор суммы |
| | Sk | Аккумулятор суммы квадратов |
| | TU1, TU2, TR1, TR2 | Текстовая переменная (для корректного вывода результатов) |
| | z | Аккумулятор суммы случайных чисел |
| | zz | Аккумулятор суммы случайных чисел |
5. Анализ полученных данных
В результате работы программы реализующей метод Монте-Карло с использованием математического моделирования получили следующие результаты:
М(Uвых)= 165.205725;
(Uвых)= 51.8301(31.374%);
Данные полученные при расчете вероятностным методом имеют следующий вид:
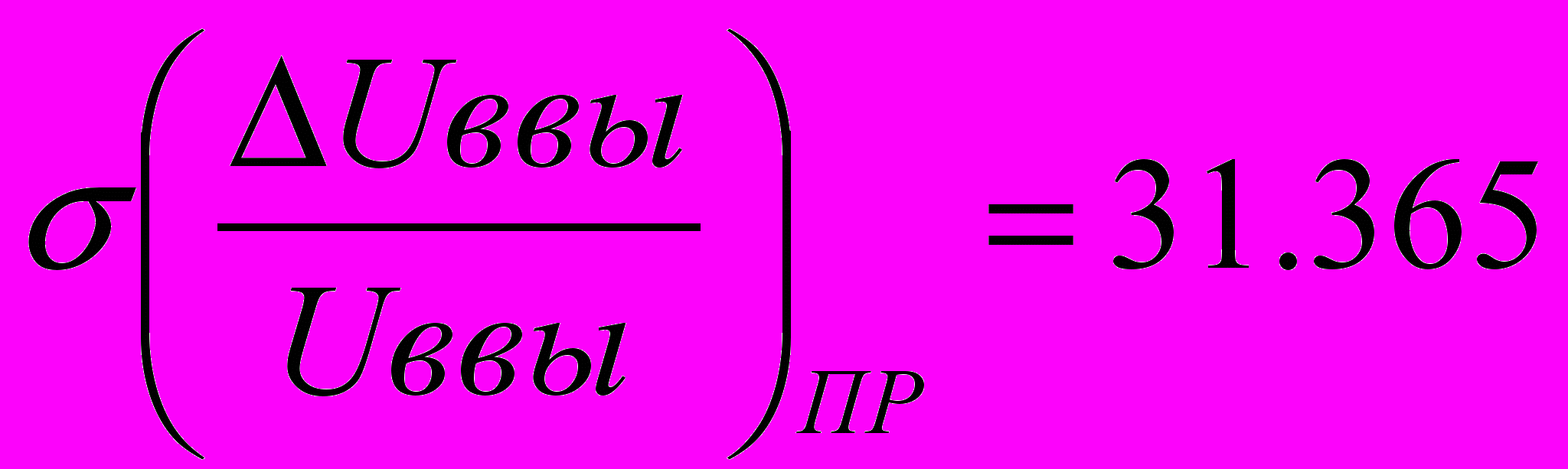%.Для контроля правильности полученных результатов проведем контрольный счет:
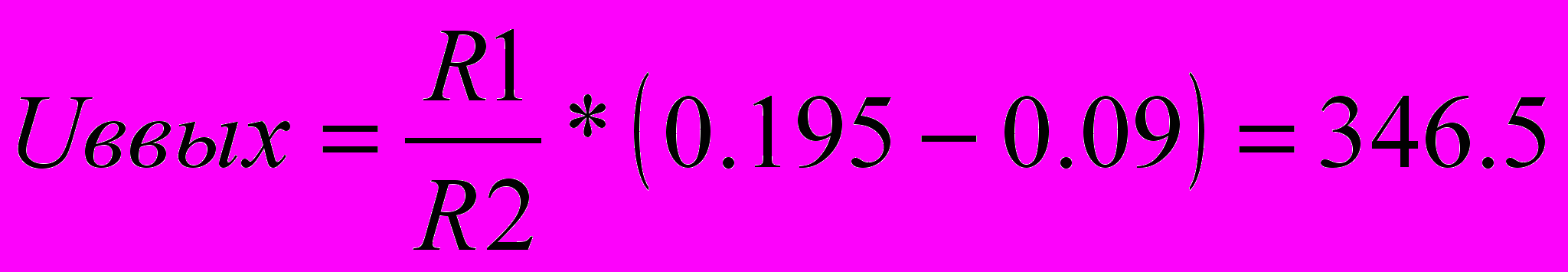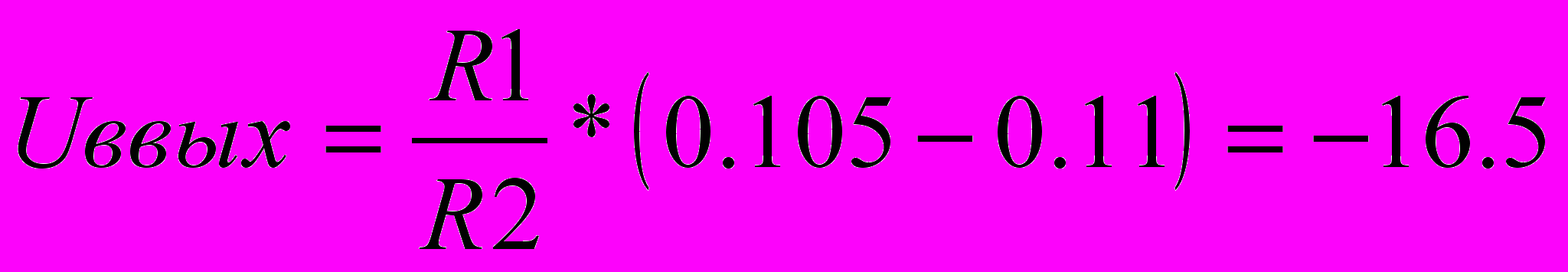мВ;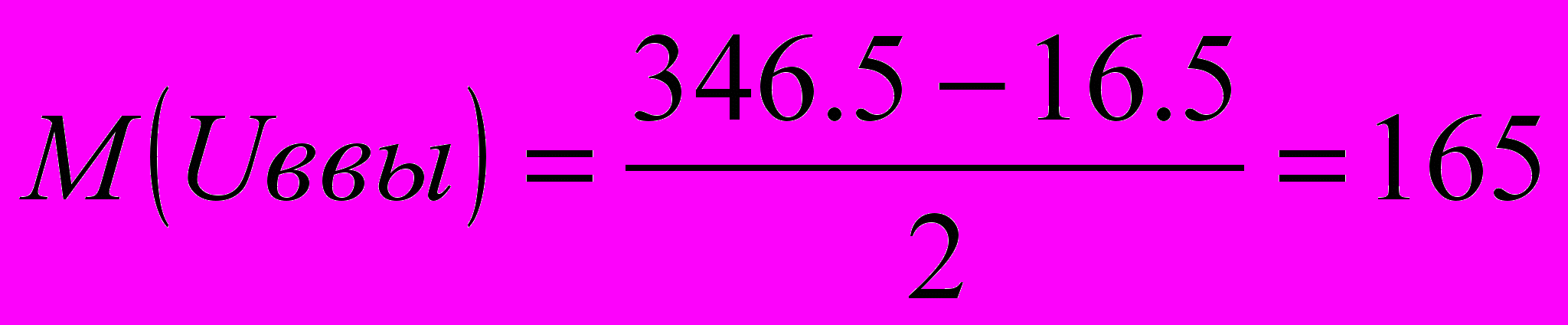
мВ;
мВ(Uвых)=60.5(36.67%).
Контрольный счет показал, что результаты полученные программой и вероятностным методом верны.
Сравнив результаты двух методов, мы видим, что разница между ними отличается на сотые доли. Можно заключить, что оба метода дают довольно-таки высокую оценку точности выходного параметра.
Заключение
Метод Монте-Карло является методом статистических испытаний, а вероятностный – расчетно-аналитическим методом. Они не исключают, а дополняют друг друга, и их необходимо разумно сочетать в инженерной практике.
Метод Монте – Карло позволяет варьировать законами распределения входных (первичных) и выходных параметров, что придает этому методе универсальность. В реализации данного метода можно численно задавать ошибку в определении математического ожидания выходного параметра, что требует только машинных затрат.
Однако не следует отбрасывать вероятностный метод расчета допусков. Он, как уже говорилось, является наиболее совершенным из расчетно-аналитических методов и позволяет наиболее правильно учитывать случайный характер как входных, так и выходных параметров.
Большое количество реализаций процесса или устройства реализовывать не выгодно из экономических соображений. Однако при малом количестве испытаний доверять, а в последствии и использовать полученные данные, нельзя из-за их неточности, вследствие недостаточности проведенных опытов.
В этом случае на помощь приходит вероятностный метод. Он позволяет с достаточной точностью решить поставленную задачу при незначительных затратах. Его точность сопоставима с точностью, получаемой при методе Монте – Карло с использованием математического моделирования, что показал данный курсовой проект.
Литература
- Боровиков С.М. Теоретические основы конструирования, технологии и надежности. -Мн.: Дизайн ПРО, 1998.-336 с.: ил.
- Методические указания к курсовой работе по курсу “Теоретические основы конструирования, технологии и надежности” для студентов специальности “ Проектирование и производство РЭС” Под ред. Боровикова С.М.-Мн.: БГУИР, 1995.-31с.
Содержание
Введение…………………………………………………..
1. Постановка задачи………………………………...
1.1. Исходные данные ……………………………………………………. 1.2.Формулировка поставленной задачи……………………………….
2.Краткое описание используемых методов ………...
2.1. Метод Монте-Карло……………………………………………………
2.2. Вероятностный метод…………………………………………………
3.Решение задачи вероятностным методом…………
4.Рализация метода Монте-Карло на ЭВМ………….
5. Анализ полученных данных………………………….
Заключение………………………………………………..
Литература…………………………………………………
Приложение……………………………………………….