Удк517 Бессеточный подход к решению краевых задач математической физики на основе метода двойного замещения с использованием атомарных радиальных базисных функций Лисин Д. А
| Вид материала | Документы |
- Нелинейные задачи математической физики, 84.09kb.
- Удк 519. 63 Метод атомарных рбф и их применение при решении задач теплопроводности, 28.05kb.
- Программа курса «уравнения математической физики» для математического отделения, 34.71kb.
- Программа по дисциплине обобщенные и специальные методы математической физики, 45.79kb.
- Isbn 978-5-7262-1377 нейроинформатика 2011, 107.92kb.
- Факультативный курс «Применение дифференциального и интегрального исчисления к решению, 69.62kb.
- Подсекция Эвентология: доцент Е. Е. Голденок, 152.9kb.
- Элективный курс по математике, 168.73kb.
- Новые нейросетевые подходы к решению краевых задач в составных областях, 31.65kb.
- Учебно-методический комплекс по дисциплине Линейные и нелинейные уравнения физики (Методы, 325.5kb.
УДК517
Бессеточный подход к решению краевых задач математической физики на основе метода
двойного замещения с использованием
атомарных радиальных базисных функций
Лисин Д.А.
Институт проблем машиностроения им .А.Н.Подгорного
НАН Украины, г.Харьков
Численные методы решения дифференциальных уравнений в частных производных в последнее время продуктивно развиваются за счет эффективного использования бессеточных подходов. Выбор этих подходов обусловлен стремлением упростить процедуру решения краевых задач в достаточно сложных геометрических 3D-областях, а также в случае исследования физических процессов с изменяющейся геометрией границ. В частности, к бессеточным подходам можно отнести метод решения дифференциальных уравнений в частных производных на основе метода двойного взаимообмена с использованием атомарных радиальных базисных функций.
Рассмотрим краевую задачу
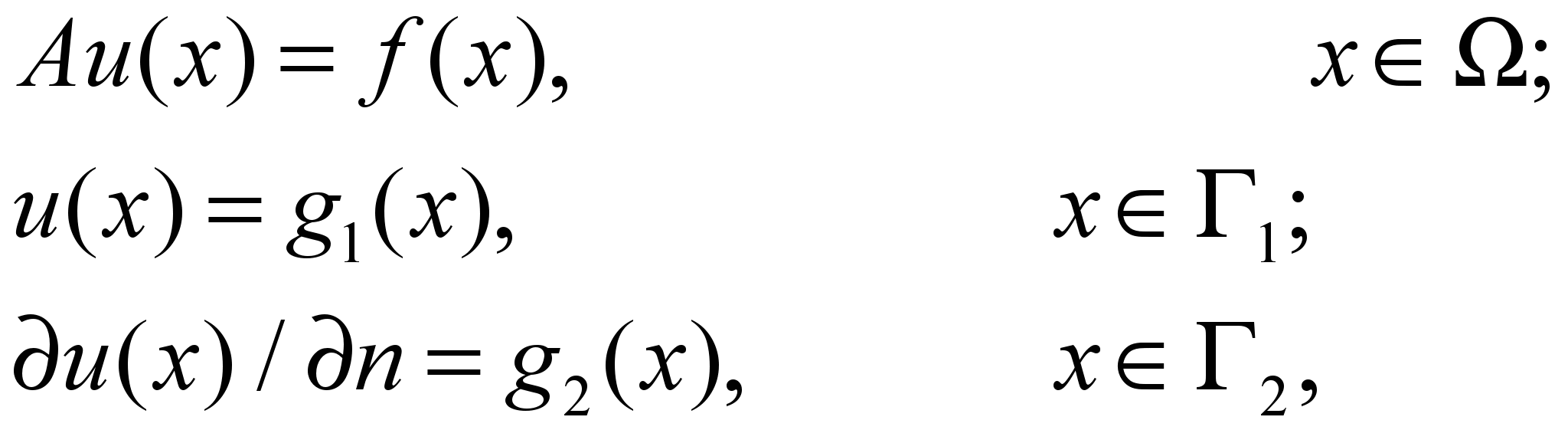
n – нормаль к поверхности Г2.
Метод двойного взаимообмена [1] заключается в разделении приближенного решения краевой задачи
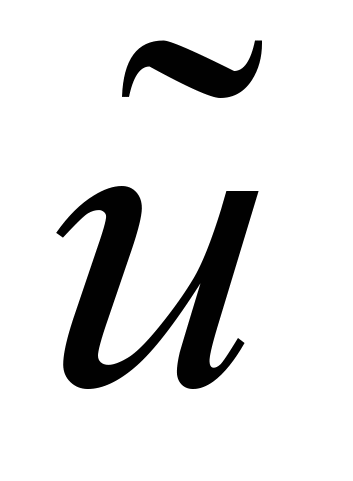на сумму двух решений 
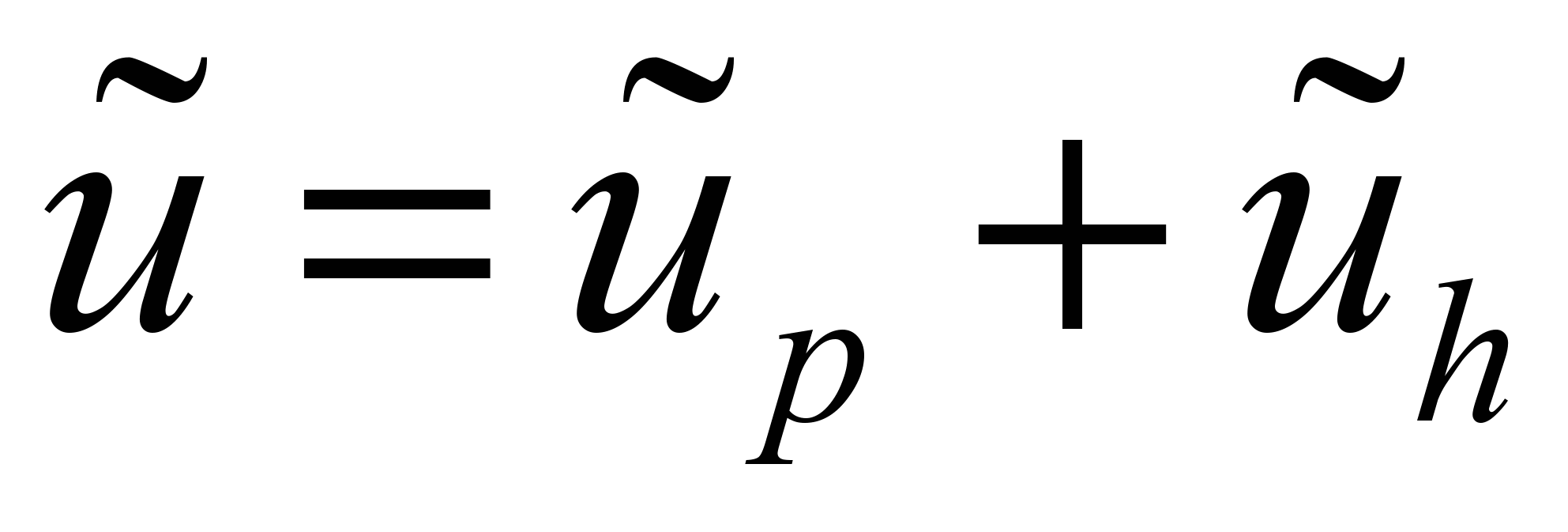, где 
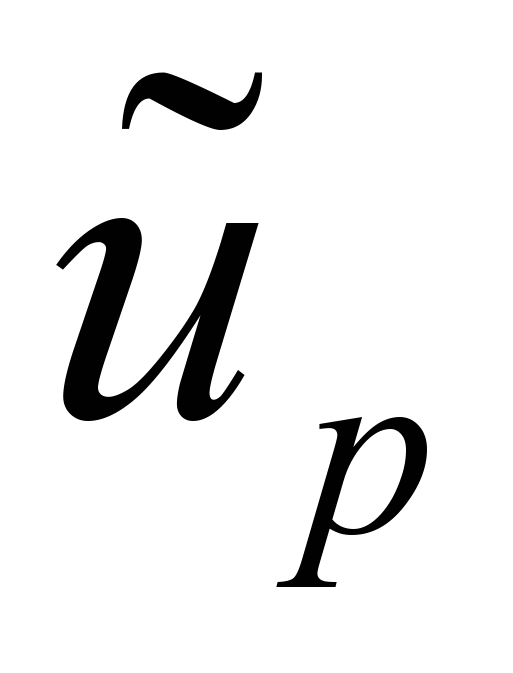- частное решение, которое должно удовлетворять дифференциальному уравнению 
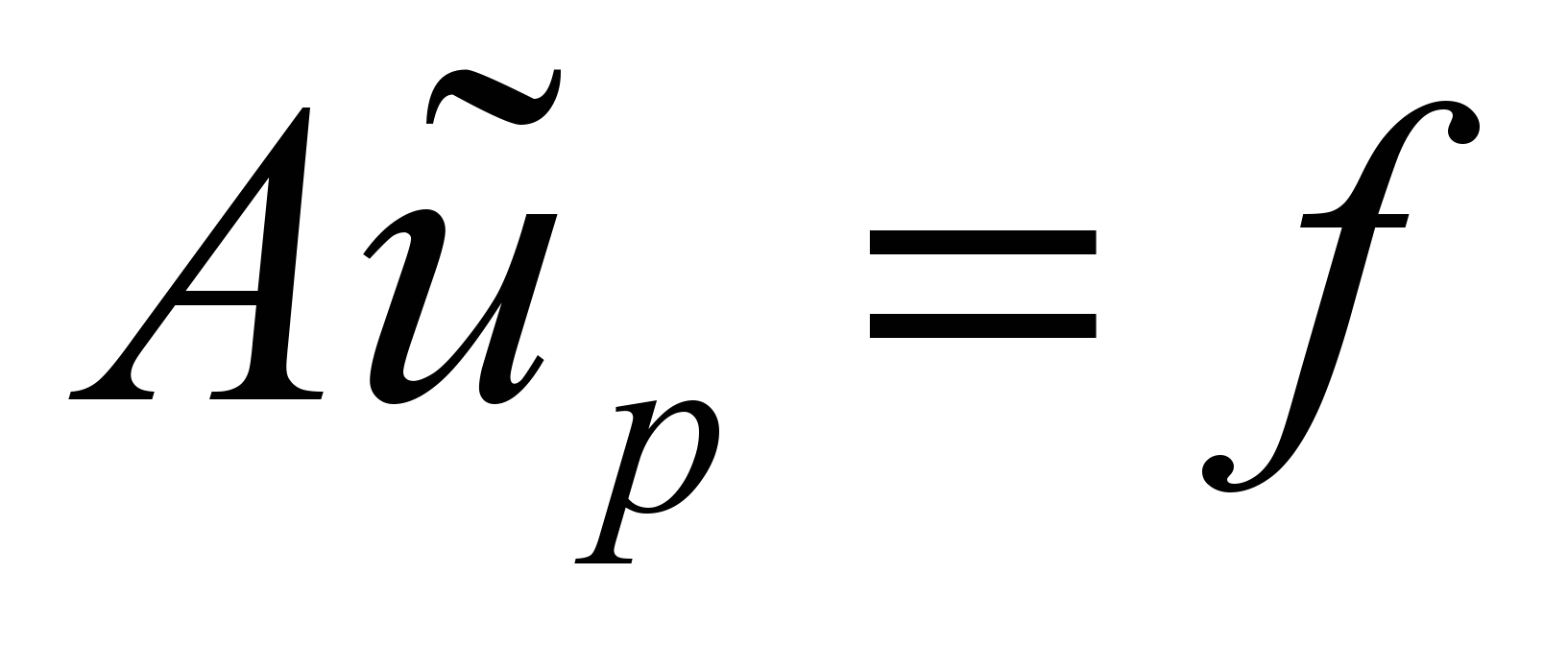внутри области, и на которое не налагаются никакие краевые условия; 
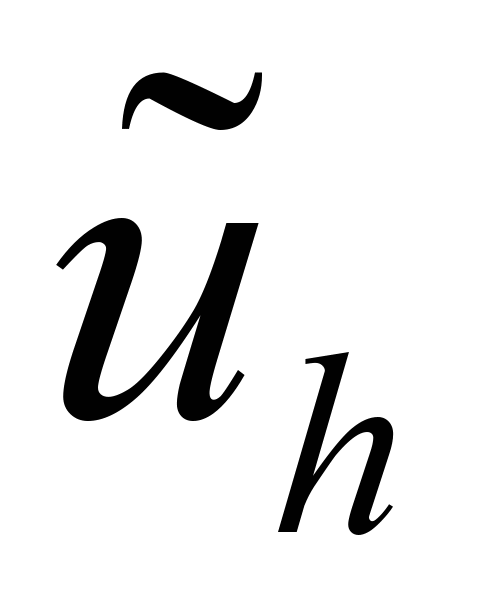- решение, удовлетворяющее однородному дифференциальному уравнению 
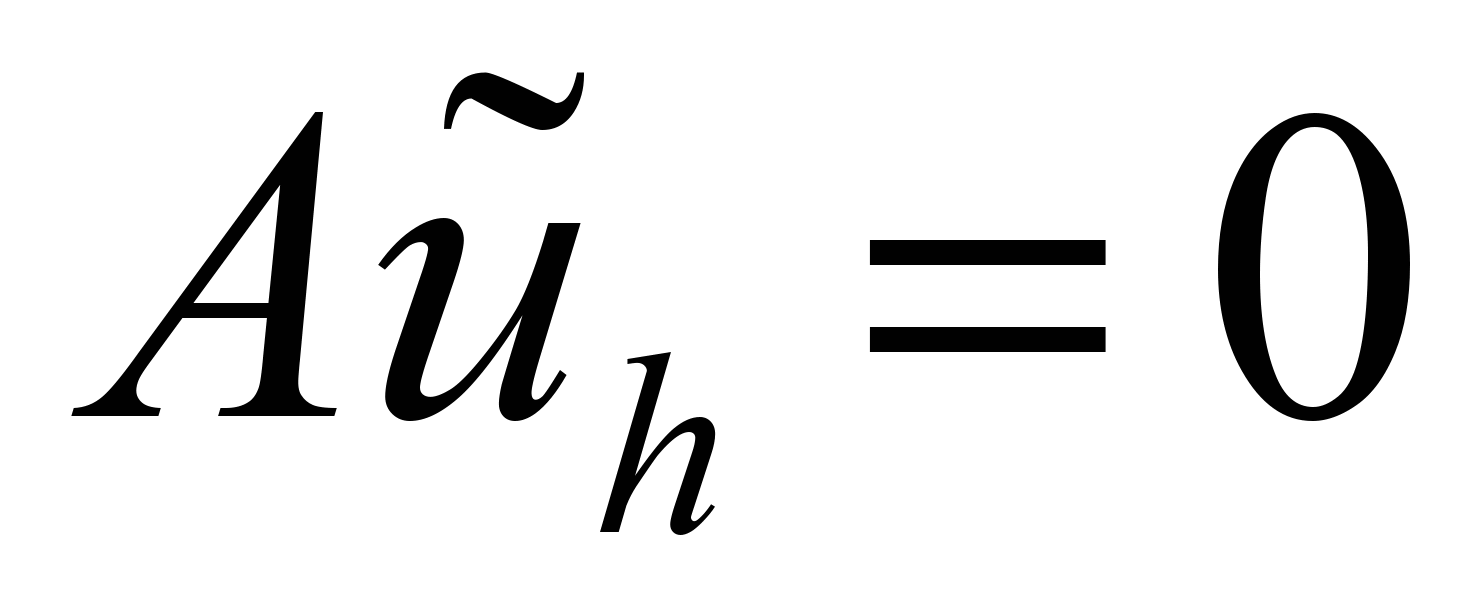внутри области с обеспечением удовлетворения заданных граничных условий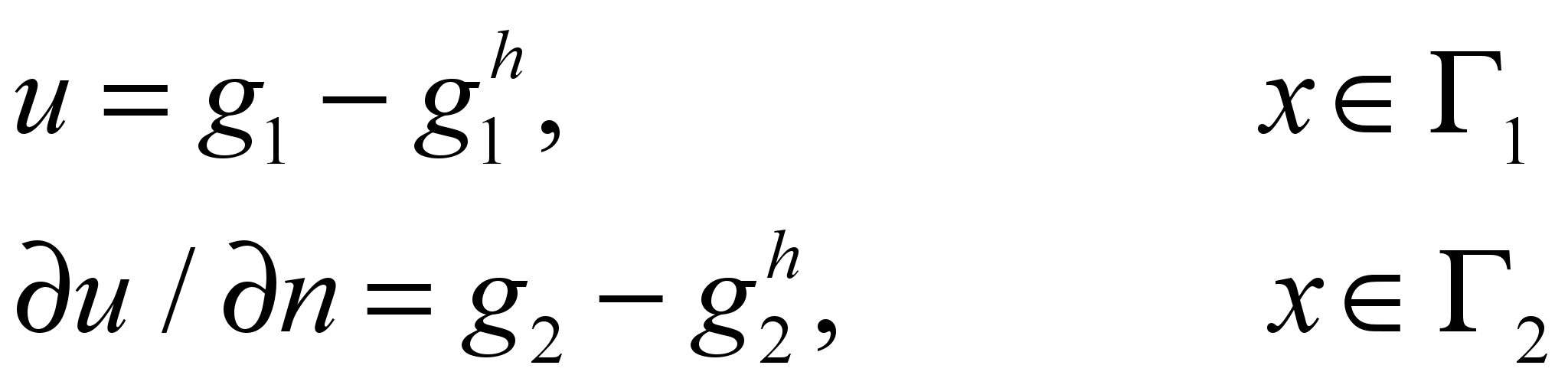
Однородное решение находится с помощью метода фундаментальных решений [1], а частное – с помощью одного из проекционных методов - метода коллокаций с использованием атомарных радиальных базисных функций.
Для решения нестационарных краевых задач управляющее дифференциальное уравнение дискретизируется по времени. Для уравнения нестационарной теплопроводности, имеющего следующий вид:
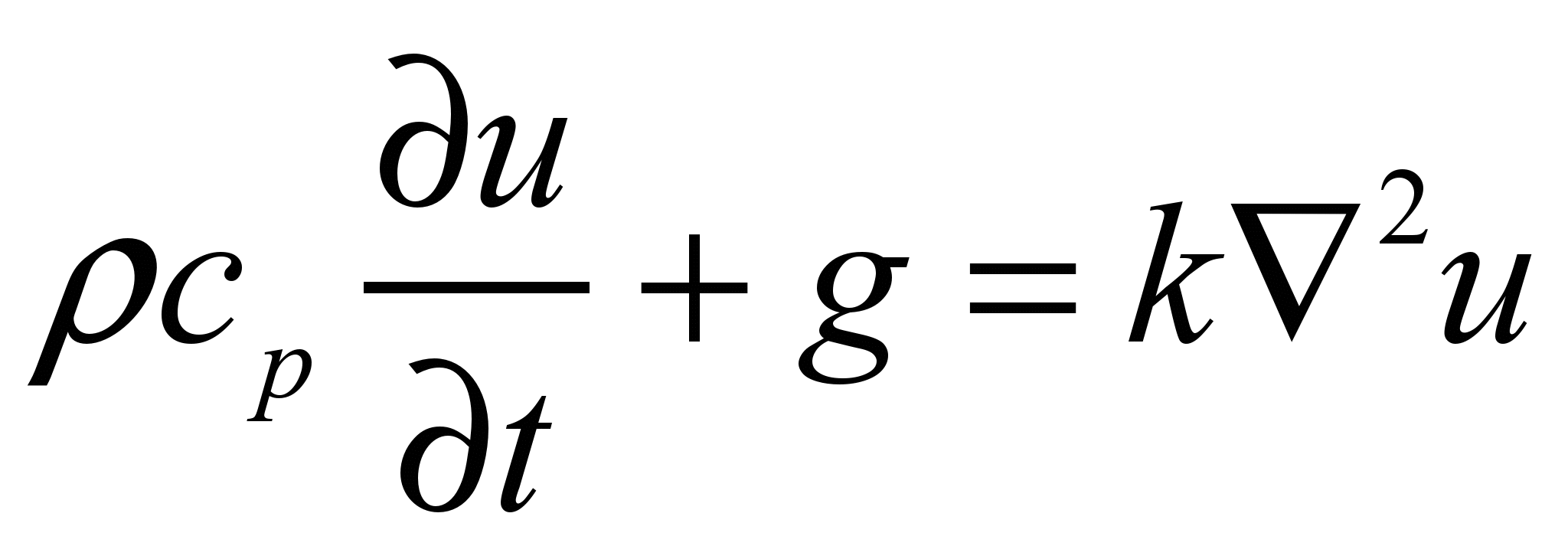,где
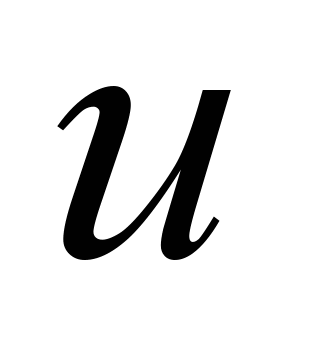- температура, 
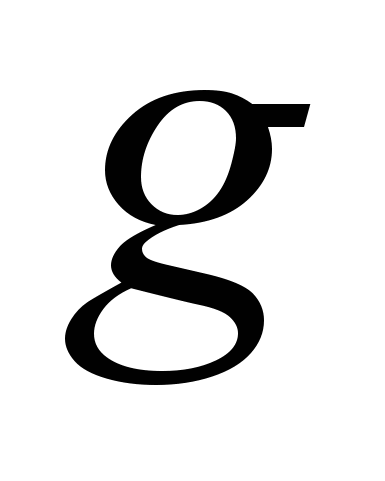- внутренний источник тепла, 
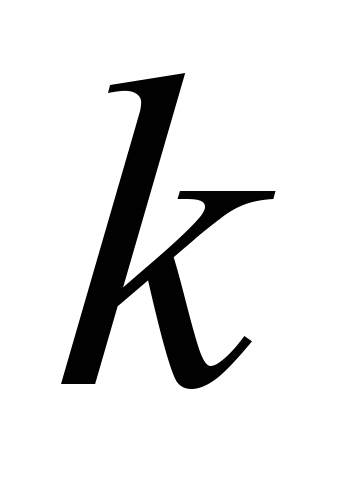- теплопроводность, 
- плотность, а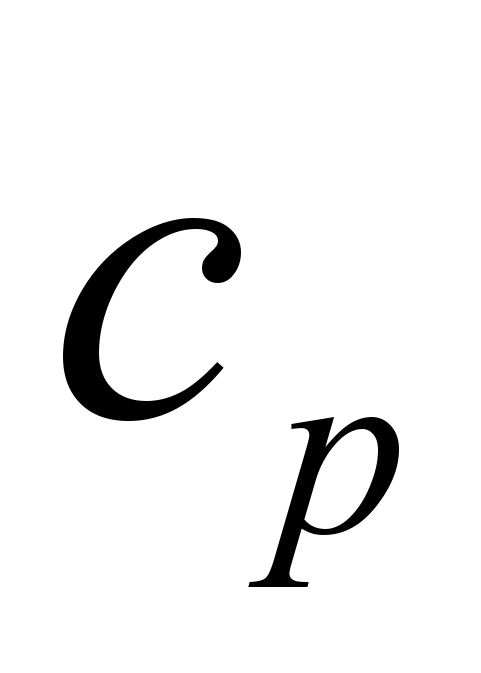 
- коэффициент температуропроводности, дискретизация по времени приводит к итерационной схеме
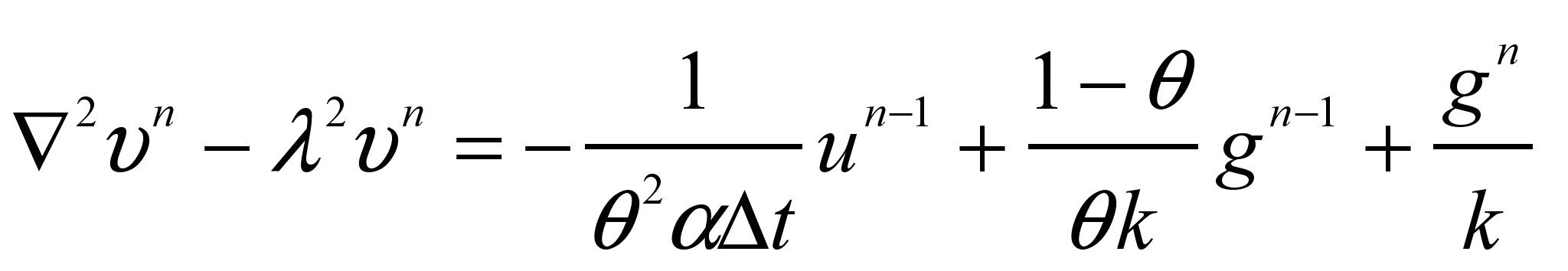, где
, 
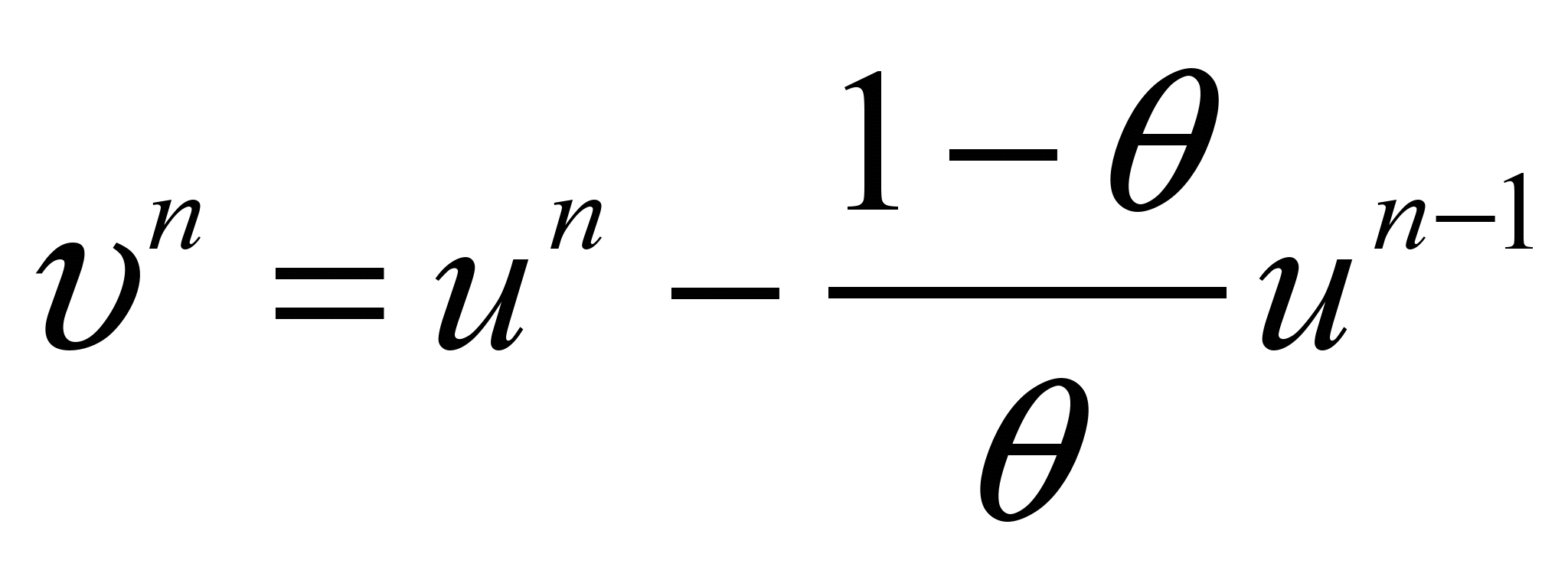- весовой коэффициент,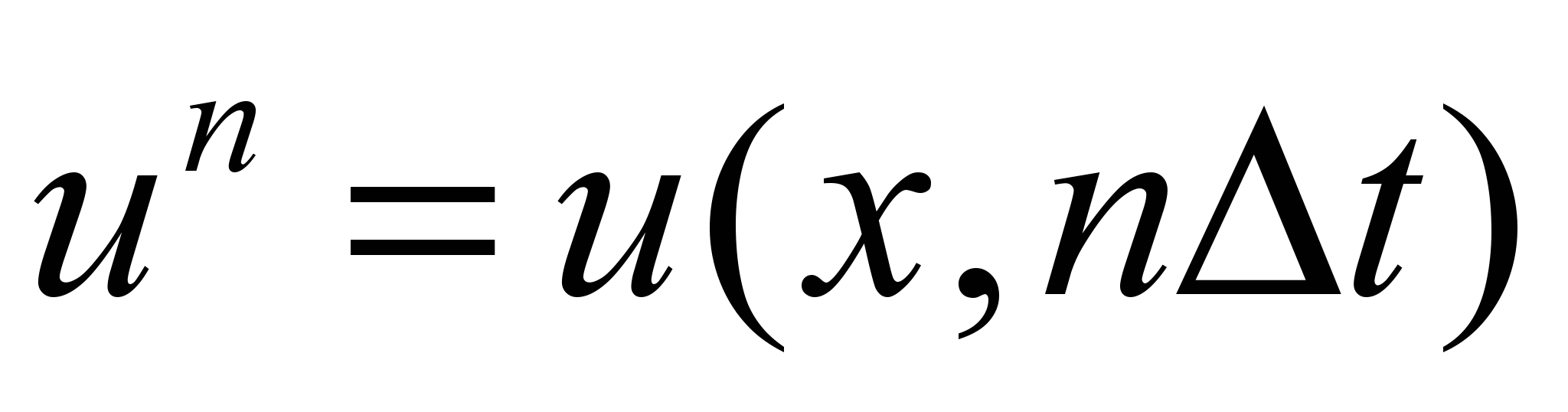 
, 
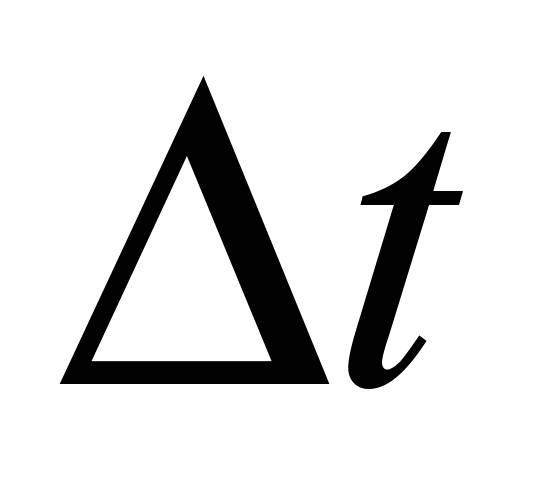- шаг по времени, 
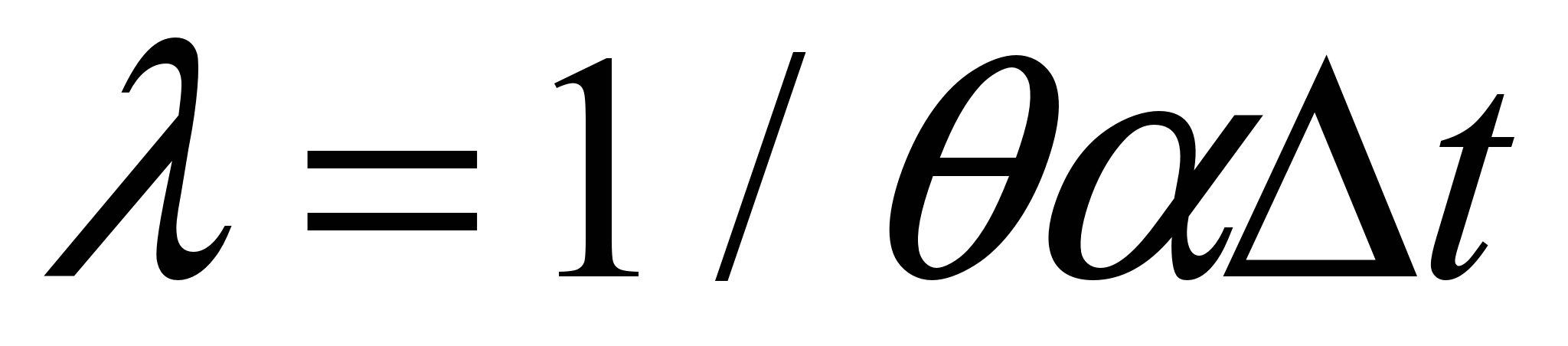, а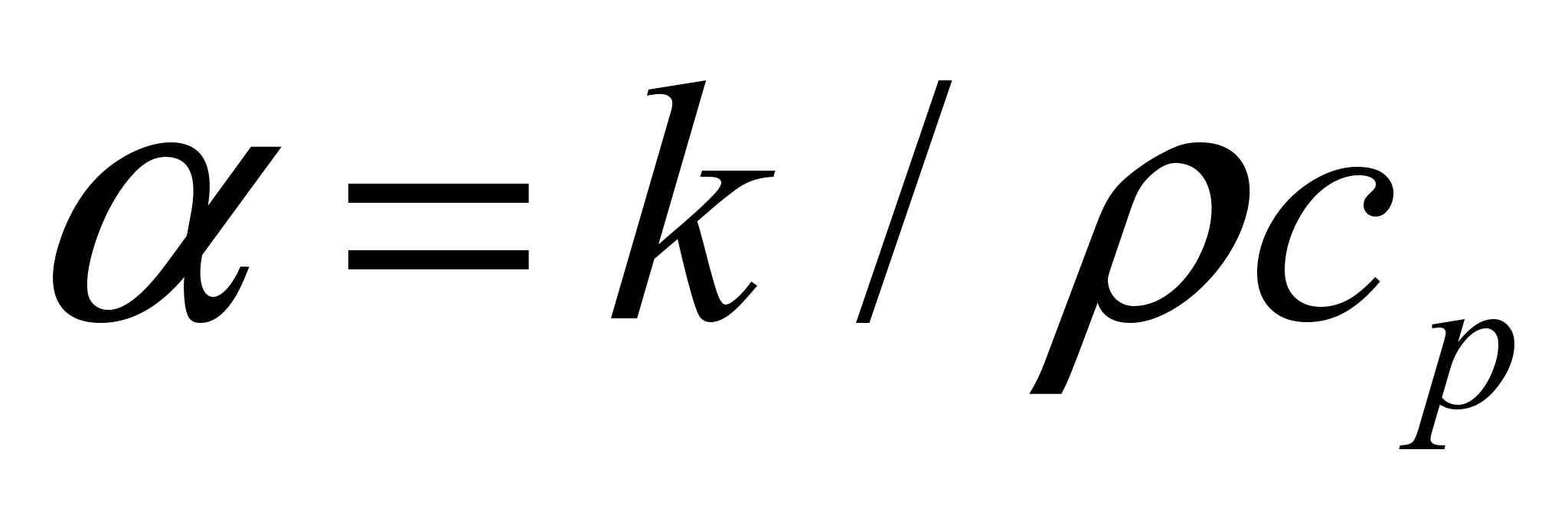 
.Таким образом, уравнение нестационарной теплопроводности сводится к последовательности неоднородных уравнений Гельмгольца. [2]
Для численного решения краевой задачи теплопроводности в сложных 3D-областях по приведенной итерационной схеме создается система компьютерного моделирования (СКМ-АФ) на основе метода двойного замещения и метода фундаментальных решений с использованием математических средств теории атомарных функций [3-4]. На рис.1 представлена твердотельная модель, созданная с помощью пакета твердотельного моделирования SolidWorks и загруженная в СКМ-АФ.
Кроме того, в СКМ-АФ применены приемы построения дискретной модели геометрических объектов с помощью математического аппарата теории R-функций, способы формирования локальных зон на поверхности объектов и узлов дискретизации, что обусловлено необходимостью задания граничных условий и условий нагружения при постановке краевых задач (рис.2).
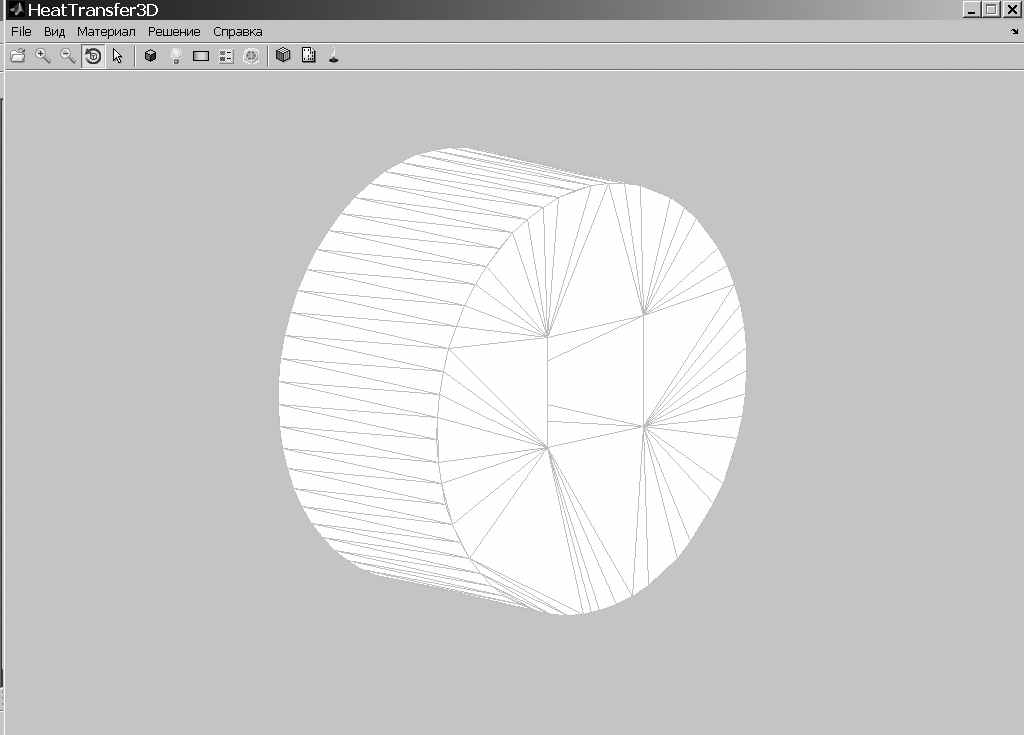
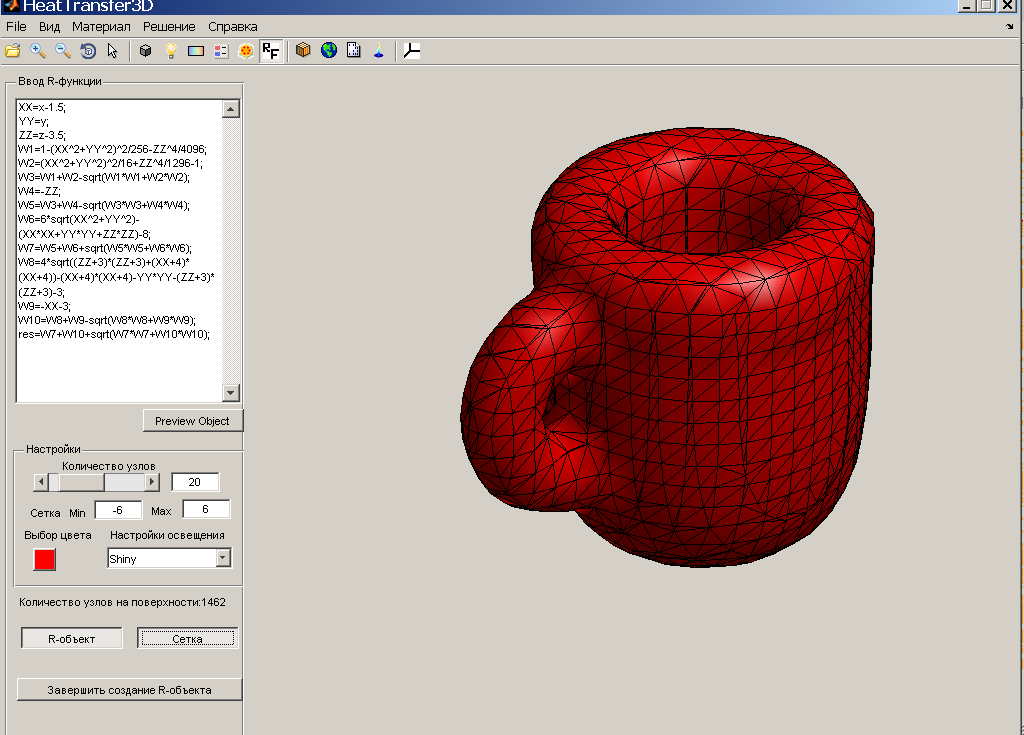
Рис.1 Рис.2
Литература
1. Bogomolny A. Fundamental solutions method for elliptic boundary value problems. SIAM Journal on Numerical Analysis 1985; 22:644-669
2. Ingber M.S., Chen C.S., Tanski J.A. A mesh free approach using radial basis functions and parallel domain decomposition for solving three–dimensional diffusion equations // International Journal For Numerical Methods In Engineering, 60, 2004. – P. 2183– 2201.
3. Колодяжний В.М., Рвачов В.О. Фінітні функції, що породжені оператором Лапласа // Доповіді НАН України. № 4, 2004. – С. 17–22.
4. Колодяжний В.М., Рвачов В.О. Деякі властивості атомарних функцій багатьох змінних // Доповіді НАН України, № 1, 2005. – С. 12–20.