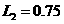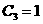Расчет переходных процессов в линейных цепях с сосредоточенными параметрами
Министерство транспорта Российской Федерации
Федеральное Государственное Образовательное чреждение
Государственная Морская Академия имени адмирала С.О. Макарова
Кафедр ТОЭ
Курсовая работ №6
У Расчет переходных процессов в линейных цепях с сосредоточенными параметрами.
Вариант № 21
Выполнил: к-т гр. Э-232
Попаденко Н.С.
Проверил: доцент, к.т.н
Попов Ю.В.
Санкт-Петербург
2005
Задана электрическая цепь, изображенная на рисунке 1:

Требуется:
1) Определить выражения для всех токов в цепи в переходном режиме, решив задачу классическим и операторным методами.
2) Определить выражения для напряжений на емкости и индуктивности, решив задачу классическим и операторным методами.
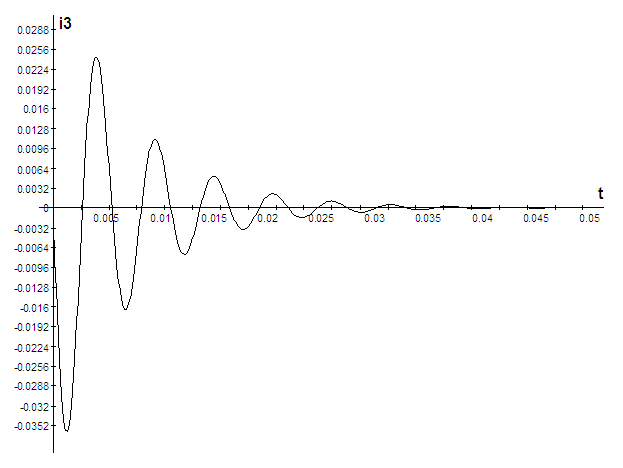
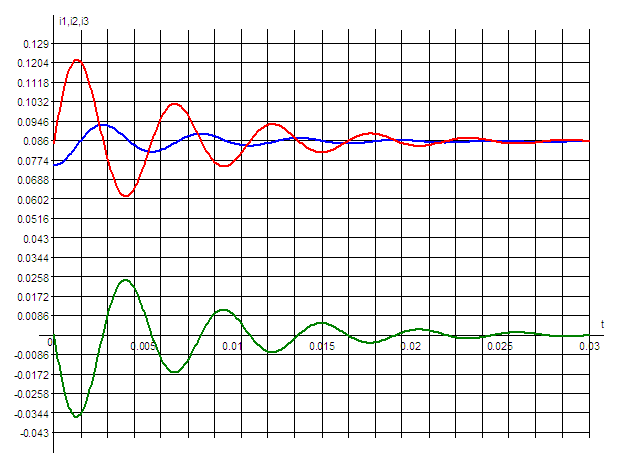
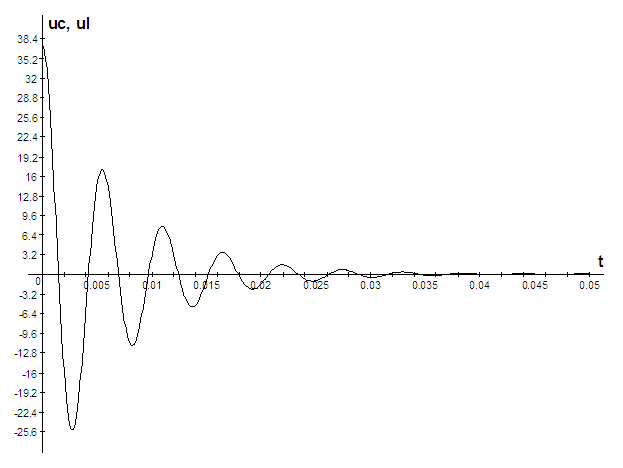
3) Построить кривые напряжения токов во всех ветвях и напряжений на емкости и индуктивностиа в функции времени.
Заданные параметры цепи:
|
|
|
|
1) Для В качестве переменных состояния рассмотрим
Приведем систему
равнений (5) к нормальной форме. 2) При (В) (А); 3) Корни характеристического равнения можно найти из выражения входного комплексного сопротивления схемы переменному синусоидальному току, т.е для 4) С помощью законов коммутации находим начальные словия переходного процесса: Подставляя эти значения в систему (6) при 5) При Решение системы дает: Искомое решение для напряжения на емкости принимает вид: налогичным образом находим решение для тока второй ветви:
При
0.075= 0.0857+ 50= Искомое выражение для тока второй ветви: Определение Согласно равнению (3)а Из системы (1): II. Операторный метод расчета 1) Составляется операторная схема замещения исходной электрической цепи (Рис.1) для времени 2) Находится изображение искомого тока. Операторная схема замещения содержит 3 источника в разных ветвях: основной и два дополнительных. Поэтому для нахождения изображения тока второй ветви воспользуемся законами Кирхгофа в операторной форме: Подставим выражения для начальных словий в систему (7). Первое равнение системы подставим во второе, выразим ток 3) По найденному изображению определяется оригинал. Для нахождения корней приравнивается к нулю выражение Искомое выражение для тока 4) Аналогично найдем ток в первой Подставим выражения для начальных словий в систему (7). Найденное выражение для тока Искомое выражение для тока 5) Найдем напряжения Искомое выражение: 6) Найдем ток третьей ветви Искомое выражение для тока: В методе переменных состояния было получено выражение для тока: Покажем, что это одно и тоже значение: 7) В случае колебательного процесса рассчитать логарифмический декремент затухания.
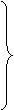
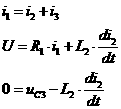 (1)
(1)
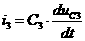 (2)
(2)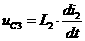 (3)
(3)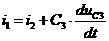 (4)
(4)
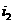 аи
аи 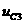
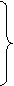
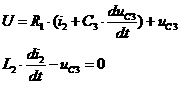 (5)
(5)
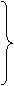

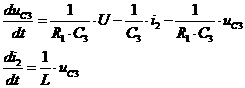 (6)
(6)
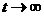 аопределим принужденные составляющие. чтем, что в становившемся режиме
аопределим принужденные составляющие. чтем, что в становившемся режиме 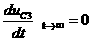 а(В/с);
а(В/с); 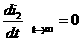 (А/с).
(А/с). Тогда система (6) примет вид:
Тогда система (6) примет вид: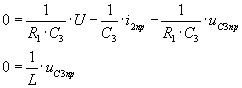
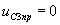
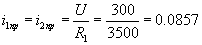
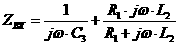 ;
;
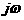 азаменяем на р и выражение приравниваем к нулю:
азаменяем на р и выражение приравниваем к нулю: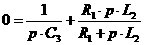
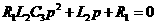
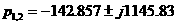
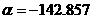 а(рад
а(рад
 (А);
(А);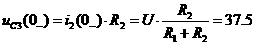
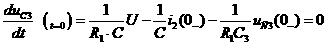
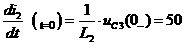
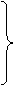 Определим постоянные интегрирования, для этого составим систему равнений. Первое равнение системы - это равнение искомой величины. Оно записывается в виде суммы принужденной и свободной составляющих. Принужденная составляющая найдена выше. Свободная составляющая записывается в соответствии с видом корней характеристического равнения. При двух комплексных сопряженных корнях свободная составляющая представляет собой затухающую синусоиду, которая содержит две постоянных интегрирования А и
Определим постоянные интегрирования, для этого составим систему равнений. Первое равнение системы - это равнение искомой величины. Оно записывается в виде суммы принужденной и свободной составляющих. Принужденная составляющая найдена выше. Свободная составляющая записывается в соответствии с видом корней характеристического равнения. При двух комплексных сопряженных корнях свободная составляющая представляет собой затухающую синусоиду, которая содержит две постоянных интегрирования А и 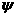
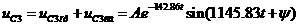
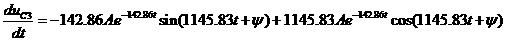
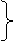

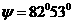 А=
37,79 (В);
А=
37,79 (В);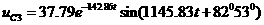 а(В).
а(В).
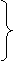
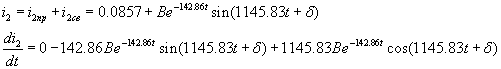
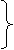
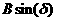
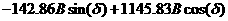
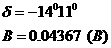
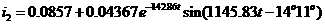 а(А);
а(А);

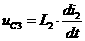
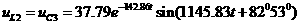 а(В);
а(В);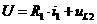
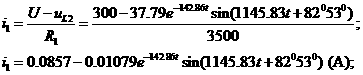


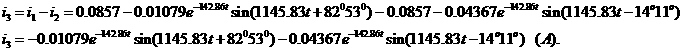
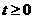
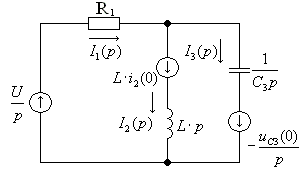
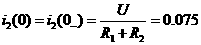 а(А);
а(А); 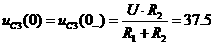
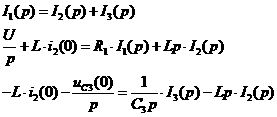 (7)
(7) аи подставим его в третье равнение системы, ав результате получили одно равнение с одним неизвестным
аи подставим его в третье равнение системы, ав результате получили одно равнение с одним неизвестным 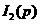

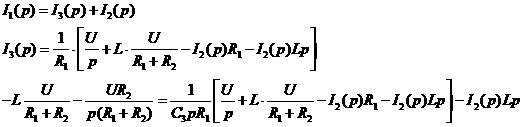
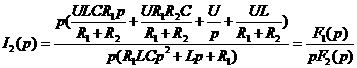
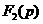
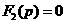
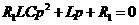
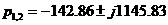
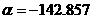 а(рад
а(рад
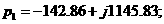
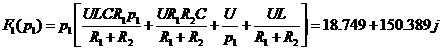
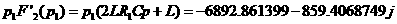
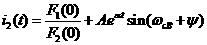 где
где 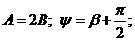
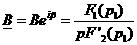

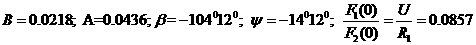
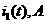
 а(А).
а(А).
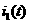 аиз системы равнений
(7).
аиз системы равнений
(7). 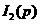 ав пункте (3) подставим во второе равнение системы (7):
ав пункте (3) подставим во второе равнение системы (7):
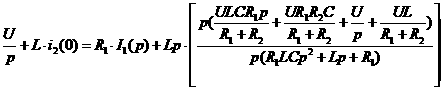
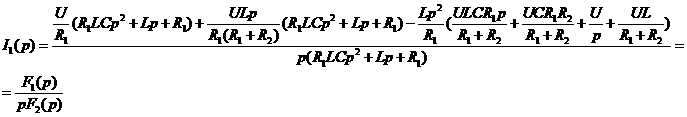
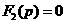
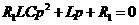
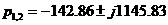
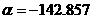 а(рад
а(рад
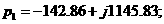
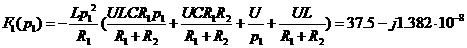
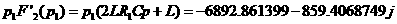
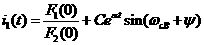 где
где 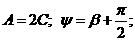
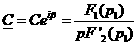

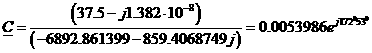
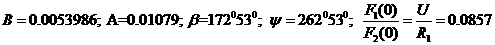
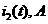
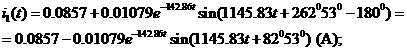 а
а
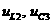 :
: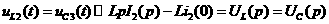
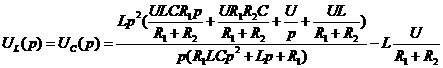
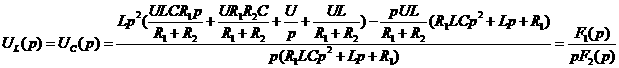
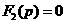
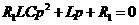
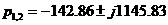
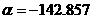 а(рад
а(рад
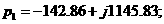
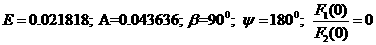
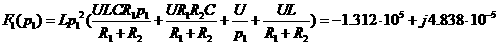
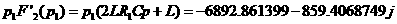
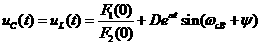 где
где 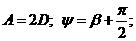
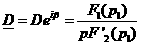

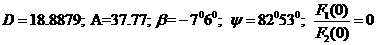
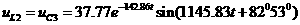 а(В);
а(В);
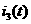
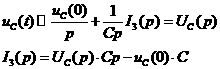
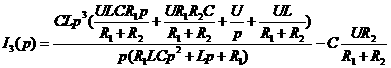
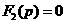
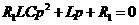
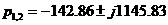
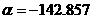 а(рад
а(рад
 где
где 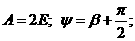
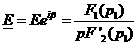
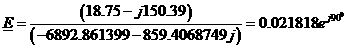
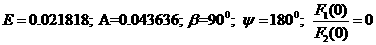

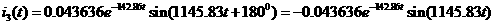
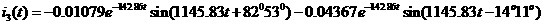

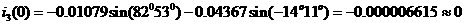

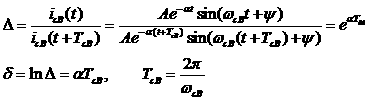
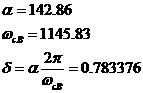
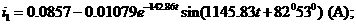
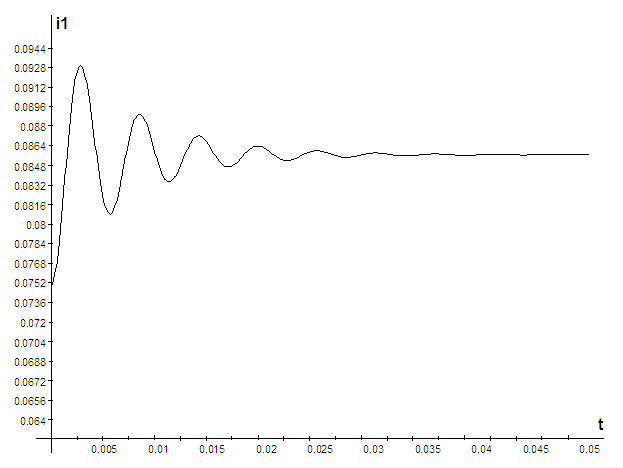
 а(А).
а(А).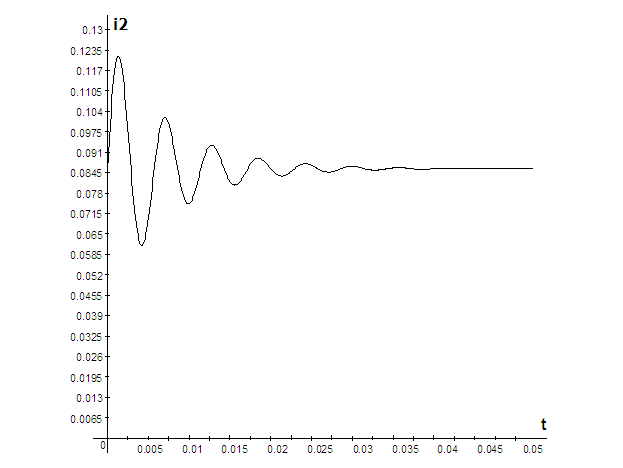
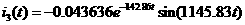
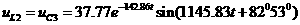


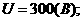
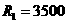 (Ом);
(Ом);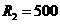 а(Ом);
а(Ом);