Міністерство освіти І науки України Кіровоградський державний педагогічний університет імені Володимира Винниченка
| Вид материала | Документы |
- Міністерство освіти І науки україни «Переяслав – Хмельницький державний педагогічний, 554.03kb.
- Міністерство освіти І науки україни двнз«Переяслав – Хмельницький державний педагогічний, 1277.11kb.
- Міністерство освіти І науки, молоді та спорту україни уманський національний університет, 29.37kb.
- Міністерство освіти І науки україни полтавський державний педагогічний університет, 680.62kb.
- Міністерство освіти І науки україни переяслав-хмельницький державний педагогічний університет, 616.99kb.
- Міністерство освіти І науки України, 1659.87kb.
- Міністерство освіти І науки україни мелітопольський державний педагогічний університет, 2525.18kb.
- Південноукраїнський державний педагогічний університет імені К. Д. Ушинського (м. Одеса), 349.4kb.
- Міністерство освіти І науки, молоді та спорту україни уманський національний університет, 30.09kb.
- Міністерство освіти І науки України Слов’янський державний педагогічний університет, 2976.14kb.
11 (2 бали). Скільки розв’язків має рівняння:
 .
. , адже в рівнянні є вираз
, адже в рівнянні є вираз  ,
,  , адже
, адже  . Звідки
. Звідки  , але
, але  . Отже,
. Отже,  . Перевіркою переконуємося, що
. Перевіркою переконуємося, що  задовольняє рівняння.
задовольняє рівняння.1
 0 (4 бали). Знайти усі трійки
0 (4 бали). Знайти усі трійки  , для яких рівняння
, для яких рівняння  має єдиний розв’язок.
має єдиний розв’язок.Якщо
 , то
, то  ,
,  (при
(при  ). У цьому випадку ми маємо один розв’язок лише тоді, коли
). У цьому випадку ми маємо один розв’язок лише тоді, коли  . Нехай
. Нехай  , для певності нехай
, для певності нехай  . Розглянемо функції
. Розглянемо функції  і
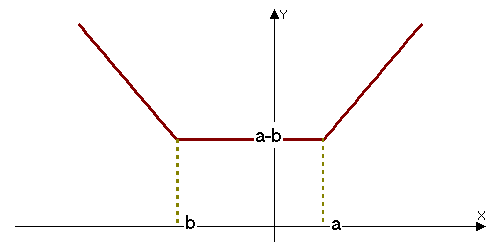
і  . Розглянувши першу функцію на проміжках
. Розглянувши першу функцію на проміжках  ,
,  ,
,  , легко побудувати її графік. Як видно з рисунка, ми маємо один розв’язок, коли
, легко побудувати її графік. Як видно з рисунка, ми маємо один розв’язок, коли  . Цей випадок розглянутий. Отже,
. Цей випадок розглянутий. Отже,  ,
,  .
.Відповідь:

9 (4 бали). Розв’язати рівняння



 .
.Виконаємо заміну:
 отримаємо:
отримаємо:  , а тоді
, а тоді 
Відповідь:

10 (4 бали). Розв’язати рівняння:
 .
.


 ; заміна
; заміна  отримаємо:
отримаємо:  .
.Відповідь:

 є двократним коренем.
є двократним коренем.Розв’яжіть самостійно:
1. Розв’язати рівняння:
 .
.Відповідь:

2. Розв’язати рівняння:
 .
.Відповідь:

3. Розв’язати рівняння:
 .
.Відповідь:

4. Розв’язати рівняння:
 .
.Відповідь:

 є двократним коренем.
є двократним коренем.5. Розв’язати рівняння:
 .
.Відповідь:

 є двократним коренем.
є двократним коренем.6. Розв’язати рівняння:
 .
.Відповідь:

11 (4 бали). Розв’язати рівняння:
 .
.

 .
.Перевіряємо:
 не є коренем, тому
не є коренем, тому .
.Виконаємо заміну:
 , отримаємо:
, отримаємо:  , а тоді
, а тоді  Відповідь:
Відповідь:  .
.Розв’яжіть самостійно:
1. Розв’язати рівняння:
 .
.Відповідь:

2. Розв’язати рівняння:
 .
.Відповідь:

3. Розв’язати рівняння:
 .
.Відповідь:
 .
.4. Розв’язати рівняння:
 .
.Відповідь:
 , корені двократні.
, корені двократні.5. Розв’язати рівняння:
 .
.Відповідь:
 .
.6. Розв’язати рівняння:
 .
.Відповідь:
 .
. 10 (4 бали). Розв’язати рівняння:
 .
.1 спосіб. (Метод Феррарі): Виокремлюємо доданки четвертого і третього степенів:
 та виділяємо повний квадрат у лівій частині:
та виділяємо повний квадрат у лівій частині:
 .
.Додамо в лівій частині у дужках деяке число
 , щоб вираз у правій частині перетворився на повний квадрат, отримаємо:
, щоб вираз у правій частині перетворився на повний квадрат, отримаємо:  або
або .
.Квадратний тричлен у правій частині перетвориться на повний квадрат, якщо його дискримінант дорівнює нулю:
 ; звідки
; звідки або
або  - маємо кубічну резольвенту. Знайдемо один (будь-який) корінь цього рівняння, наприклад, за схемою Горнера; доцільно (раціональні) корені шукати серед дільників вільного члена, крім того, у нашому випадку у зв’язку з тим, що всі коефіцієнти рівняння додатні, корені можуть бути тільки від’ємними. Тому перевіряємо лише від’ємні дільники числа 105:
- маємо кубічну резольвенту. Знайдемо один (будь-який) корінь цього рівняння, наприклад, за схемою Горнера; доцільно (раціональні) корені шукати серед дільників вільного члена, крім того, у нашому випадку у зв’язку з тим, що всі коефіцієнти рівняння додатні, корені можуть бути тільки від’ємними. Тому перевіряємо лише від’ємні дільники числа 105: . Отже
. Отже  є коренем, тому з рівняння
є коренем, тому з рівняння  маємо:
маємо: або
або  , а тоді
, а тоді .
. 2 спосіб. Метод невизначених коефіцієнтів. Переконуємося, що рівняння не має раціональних коренів (якщо старший коефіцієнт дорівнює нулю, їх шукаємо серед дільників вільного члена):
 Тоді прагнемо розкласти многочлен у добуток двох многочленів другого степеня:
Тоді прагнемо розкласти многочлен у добуток двох многочленів другого степеня:  .
.Прирівняємо коефіцієнти при відповідних степенях (вже врахували те, що найвищий степінь входить з коефіцієнтом 1):
 Якщо з першого рівняння виразити невідому
Якщо з першого рівняння виразити невідому  , з четвертого рівняння
, з четвертого рівняння  і підставити у друге та третє рівняння, отримаємо систему двох нелінійних рівнянь, з яких виключити третю невідому, отримаємо рівняння високого степеня, яке має раціональні корені:
і підставити у друге та третє рівняння, отримаємо систему двох нелінійних рівнянь, з яких виключити третю невідому, отримаємо рівняння високого степеня, яке має раціональні корені: насправді коренів декілька
насправді коренів декілька  (зауважимо, що який-небудь розв’язок можна було отримати і шляхом підбору), але розклад на множники отримаємо однозначний
(зауважимо, що який-небудь розв’язок можна було отримати і шляхом підбору), але розклад на множники отримаємо однозначний , а тоді отримаємо
, а тоді отримаємо 
Відповідь:

10 (4 бали). Нехай числа
 задовольняють умови
задовольняють умови  Знайдіть найбільше і найменше значення функції
Знайдіть найбільше і найменше значення функції  .
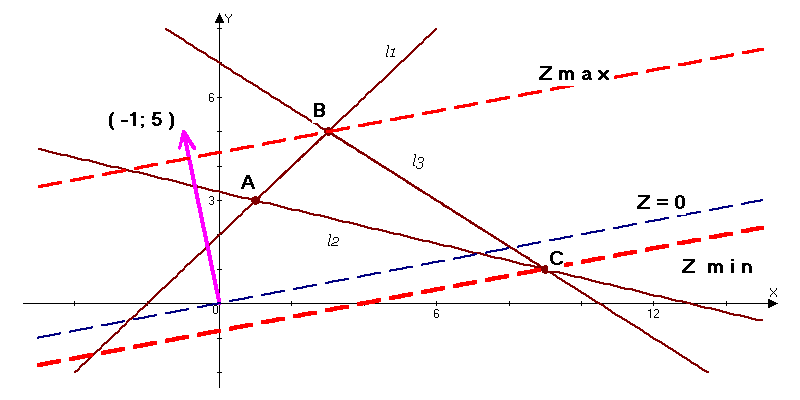
.Побудуємо прямі
 визначимо область, що задовольняє усі нерівності, це є
визначимо область, що задовольняє усі нерівності, це є  разом з внутрішньою частиною. Зобразимо на рисунку пряму
разом з внутрішньою частиною. Зобразимо на рисунку пряму  (проходить через початок координат), тоді множина
(проходить через початок координат), тоді множина  є сім’я паралельних між собою прямих, напрям зростання функції вказує нормальний вектор
є сім’я паралельних між собою прямих, напрям зростання функції вказує нормальний вектор  . Тоді найменшого значення функція досягає в точці С, найбільшого – в точці В. Визначимо координати точок В і С, розв’язавши відповідно, системи рівнянь:
. Тоді найменшого значення функція досягає в точці С, найбільшого – в точці В. Визначимо координати точок В і С, розв’язавши відповідно, системи рівнянь: 

А тоді

11 (4 бали). Нехай числа
 задовольняють умови
задовольняють умови  Знайдіть всі значення, яких можуть приймати а)
Знайдіть всі значення, яких можуть приймати а)  ;
;  б)
б)  ; в)
; в)  (3 задачі).
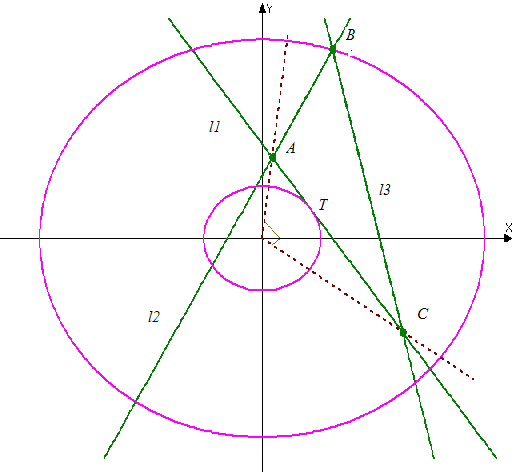
(3 задачі).Побудуємо прямі
 та вкажемо частини площини, що задовольняють усі умови задачі.
та вкажемо частини площини, що задовольняють усі умови задачі. Нескладно показати, що це є трикутник
 , разом з внутрішньою частиною. Координати точок вершин трикутника
, разом з внутрішньою частиною. Координати точок вершин трикутника  знайдемо, розв’язавши системи:
знайдемо, розв’язавши системи: ;
; 
 .
.а) Невідома
 змінюється від абсциси точки А до абсциси точки С, тобто
змінюється від абсциси точки А до абсциси точки С, тобто ; аналогічні міркування приводять до висновку:
; аналогічні міркування приводять до висновку:  .
.б) Щоб взнати межі зміни невідомої
 (
( є коло з центром в початку координат та радіусом с), знайдемо точки площини трикутника АВС, що розташовані найближче і найдалі від центру кола, т. О);
є коло з центром в початку координат та радіусом с), знайдемо точки площини трикутника АВС, що розташовані найближче і найдалі від центру кола, т. О); рівняння
 , тоді кутовий коефіцієнт прямої ОТ, що перпендикулярна до
, тоді кутовий коефіцієнт прямої ОТ, що перпендикулярна до  , рівняння ОТ:
, рівняння ОТ:  . Тоді
. Тоді  , звідки
, звідки  - а тоді найменше значення
- а тоді найменше значення  . Найбільше значення
. Найбільше значення  досягає в точці В і дорівнює
досягає в точці В і дорівнює  .
. Зауваження. Відстань від прямої
 до початку координат можна було простіше, не обчислюючи точки Т, якщо записати рівняння
до початку координат можна було простіше, не обчислюючи точки Т, якщо записати рівняння  у нормальному вигляді
у нормальному вигляді  , причому права частина (вільний член) обов’язково має бути додатним, він і показує відстань до початку координат
, причому права частина (вільний член) обов’язково має бути додатним, він і показує відстань до початку координат 
 .
.в)
 є рівняння прямої, що проходить через початок координат, кутовий коефіцієнт дорівнює с. Очевидно, кутовий коефіцієнт є найменшим для прямої ОС,
є рівняння прямої, що проходить через початок координат, кутовий коефіцієнт дорівнює с. Очевидно, кутовий коефіцієнт є найменшим для прямої ОС,  і найбільшим для прямої ОА,
і найбільшим для прямої ОА,  . А тому
. А тому  .
.9 (7 балів). Знайти найбільше і найменше значення виразу
 , якщо
, якщо 
Нехай
 виразимо
виразимо  і
і  , отримаємо
, отримаємо  Врахуємо обмеження, дані в умові, матимемо:
Врахуємо обмеження, дані в умові, матимемо:  звідси
звідси  Побудуємо відповідну множину точок в системі
Побудуємо відповідну множину точок в системі  : Отримаємо паралелограм
: Отримаємо паралелограм  . Врахувавши, що
. Врахувавши, що  - тангенс кута н
- тангенс кута н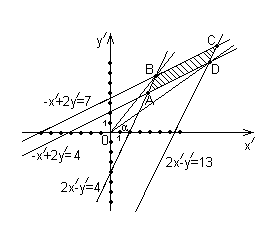 ахилу прямої, що проходить через точки
ахилу прямої, що проходить через точки  ;
;  , маємо, що
, маємо, що  набуває найменшого значення в точці
набуває найменшого значення в точці  , що є точкою перетину прямих
, що є точкою перетину прямих  звідси
звідси  ;
; 
 ;
;  ;
;  досягає найбільшого значення в точці
досягає найбільшого значення в точці  :
: 
 ;
;  .
.